Высшая математика - часть 1 [технические специальности] 1-курс КР-3 в-1

Вариант 1

Задача 101. Построить график функции y = f (x) преобразованием графика функции y = sin x :

y = 3sin(2x −1)

Решение. y = sin x :

y = 3sin x :

y = 3sin(2x −1):

1

Задача 111. Дана функция r = f (ϕ) на отрезке 0 ≤ ϕ ≤ 2π . Требуется: 1) построить

график функции в полярной системе координат по точкам, давая ϕ значения через промежуток π /8, начиная от ϕ =0; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.

Решение.

Составим таблицу значений функции:

				ϕ										r(ϕ)
		0,2π												-
		π	,				15π							39,41
8
									8
		π		,				7π						10,24
4									4
	3π			,				13π						4,86
8									8
		π		,				3π						3
2									2
	5π			,				11π						2,17
8									8
		3π			,				5π					1,76
4									4
		7π				,			9π					1,56
8									8
				π										1,5

Строим чертеж:

2

Замена координат:

	r =		, cosϕ =			x
		x2 + y2						.
					x2	+ y2

Подставляем:

r(1- cosϕ) = 3

x2 + y2 = 3 + x

Возводим обе части в квадрат:

x2 + y2 = 9 + 6x + x2

y2

= 9 + 6x

2

æ

3

ö

y

= 6ç x

+

÷

2

Получили параболу.

è

ø

Задача 121. Найти указанные пределы, не пользуясь правилом Лопиталя.

2x3

+ 7x2 - 2

æ ¥

ö

2x + 7 - 2 / x

2

¥ + 7 - 0

а) lim

=

ç

÷ = lim

=

= ¥ .

6x2

- 4x + 3

¥

6 - 4 / x +

3/ x2

6

- 0 +

0

x→∞

è

ø

x→∞

x2 + x -12

æ 0 ö

(x + 4)(x - 3)(

+

)

x→3

x→3

x - 2

4 - x

x - 2 - 4 - x

è

0 ø

( x - 2 - 4 - x )(

x - 2 + 4 - x )

б) lim

= ç

÷

= lim

=

= lim

(x + 4)(x - 3)(

+

)=

1

× lim((x + 4)(

+

))=

(3 + 4)(1+1)

x - 2

4 - x

= 7.

x - 2

4 - x

2

x→3

(x - 2 - 4 + x)

x→3

2

sin 2

x

0 ö

1

sin 2

x

1

1

æ

4

2

в) lim

4

= ç

÷

=

× lim

=

×1

=

.

x2

16

16

16

x→0

è

0 ø

x→0 æ x

ö2

ç

÷

è 4

ø

Воспользовались пределом: lim

sin t

= 1.

t→0

t

x

= (1∞ )= lim

é

1

ù2x

lim 2x

г) lim(3 - 2x)

ê(1+ 2

- 2x)

ú

= ex→1

= e2 .

1−x

2−2x

x→1

x→1

ë

û

Воспользовались пределом: lim(1+ t)1/ t

= e .

t→0

3

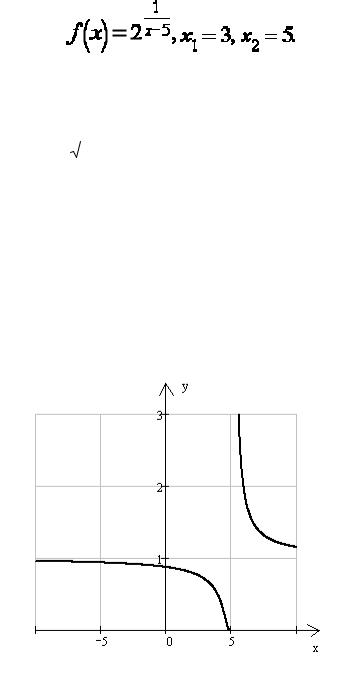
Задача 131. Заданы функция y = f (x) и два значения аргумента x1 и x2 . Требуется:

1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа; 3) сделать схематический чертеж.

Решение.

Вычисляем односторонние пределы:

	- для x1		= 3:
	1		1		1			1
	lim 2	x−5	= lim 2	x−5	= 2	3−5	=			.
	x→3−0		x→3+0					2

Так как переделы равны и конечны, в этой точке нет разрыва. - для x2 = 5:

	1					ét =	1		; x ® 5 - 0 Þ t ® -¥ù	= lim 2t = 0 ,
lim	2		x−5		=
x→5−0						ê	x - 5	ú		t→−∞
						ë		û
	1					ét =	1		; x ® 5 + 0 Þ t ® +¥ù	= lim 2t = +¥ .
lim	2		x−5		=
x→5+0						ê	x - 5	ú		t→+∞
						ë		û

Так как переделы не равны и один из них равен бесконечности, в точке x2 = 5 - разрыв

второго рода. Строим чертеж:

4

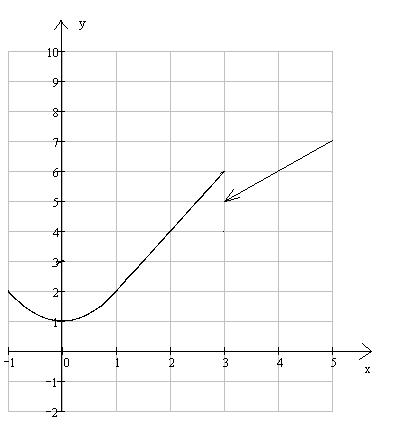
Задача 141. Задана функция y = f (x) различными аналитическими выражениями для

различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

ìx2 +1, x £ 1,

y= ïí2x,1 < x £ 3, ïîx + 2, x > 3.

Решение.

Так как все функции, составляющие функцию y = f (x), непрерывны в любой точке, то единственно возможными точками разрыва могут быть только x1 = 1 и x2 = 3. Вычисляем односторонние пределы:

- для x1 = 1:

lim	y(x) = lim(x2 +1)= 12 +1 = 2 ,
x→1−0	x→1
lim	y(x) = lim(2x) = 2 ×1 = 2 .
x→1+0	x→1

Так как переделы равны и конечны, в этой точке нет разрыва. - для x2 = 3:

lim y(x) = lim(2x) = 2 ×3 = 6 ,

x→3−0 x→3

lim y(x) = lim(x + 2) = 3 + 2 = 5.

x→3+0 x→3

Так как переделы не равны и конечны, в точке x2 = 3 - разрыв первого рода. Строим чертеж:

5

Список использованных источников

1.Власов В.Г. Конспект лекций по высшей математике. - М.: Айрис, 1996.

2.Высшая математика: Общий курс: Учебник / А.В.Кузнецов, Л.Ф.Янчук, С.А.Мызгаева и др.; Под общей редакцией профессора А.И.Яблонского. - Мн.:

Выш. шк., 1993.

3.Дадаян А.А., Дударенко В.А. Алгебра и геометрия: Учеб. пособ. - Мн.: Выш. шк., 1989.

4.Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики: Учеб. пособ. для вузов - М: Наука, 1989.

6