3.8. Обратные функции. Производная обратной функции

Пусть задана функция с областью определения и множеством значений . Если каждому значению ставится в соответствие единственное значение , то определена функция с областью определения и областью значений , называемая обратной по отношению к функции . Про функции и говорят, что они взаимно обратные. Если возможно решить уравнение относительно , то по исходной функции можно найти обратную функцию. Например, для функции обратной функцией будет функция . Однако, если, как обычно, независимую переменную обозначить через , а зависимую переменную через , то функция, обратная функции , запишется в виде . В последнем примере для функции обратной будет функция .

Для существования взаимно однозначного соответствия между множествами и необходима монотонность функции. Если функция возрастает (убывает), то и обратная функция тоже возрастает (убывает). Следует отметить, что если графики взаимно обратных функций и совпадают, то графики функций и симметричны относительно биссектрисы угла первой четверти.

Теорема. Если функция строго монотонна на промежутке и имеет неравную нулю производную в любой точке этого промежутка, то обратная ей функция также имеет производную в соответствующей точке, определяемую равенством .( )

Доказательство. Рассмотрим обратную функцию . Пусть аргумент и функция испытывают приращения и . Поэтому можно записать

.

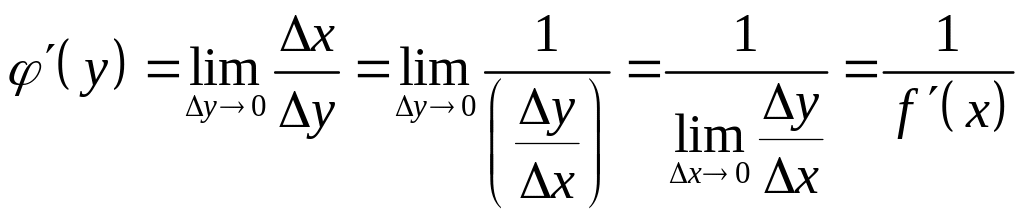Таким образом, производная обратной функции равна обратной величине производной исходной функции.

Используем теорему о дифференцировании обратной функции для нахождения производной логарифмической функции . Рассмотрим функцию с известной производной . Тогда для обратной функции можно указать производную . Поменяв на , затем, перейдя к привычным обозначениям для аргумента и функции, получим:

.

В частном случае для натурального логарифма имеем:

.

Аналогичным образом могут быть получены производные обратных тригонометрических функций. Например, для функции обратной функцией является функция . Тогда

.

Подобным образом получаем:

, , .

3.9. Производная сложной функции

Пусть и , тогда является сложной функцией с промежуточным аргументом и независимым аргументом .

Теорема. Если функция имеет производную в точке , а функция имеет производную в точке , то сложная функция имеет производную в точке , находящуюся по формуле

.

Доказательство. Поскольку , то , где при , причем .

Для функции , имеющей производную в точке , можно записать , где .

Подставив значение в выражение для имеем

.

Рассмотрим предел

.

Таким образом, производная сложной функции равна .

3.10. Гиперболические функции и их производные

В механике встречаются гиперболические функции, определяемые следующими формулами: гиперболический синус

,

гиперболический косинус (цепная линия)

,

гиперболический тангенс

,

гиперболический котангенс

.

Между гиперболическими функциями существуют соотношения, аналогичные соотношениям между тригонометрическими функциями:

;

;

;

;

.

Найдем производные гиперболических функций:

;

;

;

;