Вопрос №1. Опишите способы задания движения точки и связь между ними. Как найти уравнение траектории точки?

Движение точки в пространстве определяется тремя ос­новными способами: векторным, координатным и естествен­ным. Векторный способ задания движения применяется при тео­ретических исследованиях, координатный и естественный упот­ребляются преимущественно при решении задач.

Векторный способ задания движения точки

Выберем некоторый неподвижный центр О и проведем из этого центра в точку М, движение которой изучаем, радиус-вектор r (рис. 2.1). При движении точки М радиус-вектор r изме­няется по величине и по направлению. Каждому моменту време­ни t соответствует определенное значение r

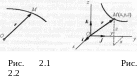
Следовательно, радиус-вектор г однозначно определяет, положение точки М. Таким образом, чтобы определить "движение точки, нужно задать ее радиус-вектор в виде однозначной и не­прерывной функции времени:

r=r(t);

Уравнение (1) определяет положение точки М в про­странстве в произвольный момент времени и, следовательно, уравнение (1) определяет закон движения точки М. При вектор­ном способе задании движения траекторией точки будет годо­граф радиус-вектора r.

Координатный способ задания движения точки

Рассмотрим прямоугольную декартову систему коорди­нат. Положение движущейся точки М определяется координата­ми х, у, z (рис. 2.2). Если координаты точки заданы как однознач­ные функции времени x = x(t), y=y(t), z = z(t), (2)

то положение точки М в пространстве известно в каждый момент времени. Уравнения (2) определяют закон движения точки и на­зываются уравнениями ее движения. С математической точки зрения уравнения (2) представляют собой параметрические урав­нения траектории точки. Чтобы найти уравнение траектории в форме зависимостей между координатами точки М, нужно из уравнений (2) исключить время, т.е. параметр t. Решая, например, последнее уравнение из (2) относительно t , найдем t = ф (z). Подставляя это соотношение в первые два уравнения, получим х = х[ф(z)]; y=у[ф(z)]-

Эти уравнения являются уравнениями поверхностей, пе­ресекающихся вдоль траектории точки.

Если точка движется в плоскости Оху, ее движение опре­деляется двумя уравнениями: x = x(t), y = y(t).

Если же точка движется по прямой, ее положение можно опреде­лить одной координатой, например: х = x(t).

Кроме декартовой системы координат, употребляются и другие координатные системы. Например, на плоскости можно пользоваться полярной системой координат (р, ф). В этих коор­динатах уравнения движения точки имеют вид: р = р(t), Ф = ф(t)

где р - полярный радиус; ф - угол между полярной осью и по­лярным радиусом.

Между координатным и векторным способами задания движения точки существует связь. Это видно, если записать раз­ложение радиус-вектора r по ортам i, j, k декартовой системы координат: r = x(t)i + y(t)j + z(t)k. (7)

Равенство (7) устанавливает зависимость радиус-вектора точки М от времени и решает вопрос о переходе от координатно­го способа задания движения точки к векторному.

Естественный способ задания движения точки

Этот способ задания движения точки применяется в том случае, когда траектория точки, относительно выбранной системы отсчета, известна. Выберем на этой траектории какую-нибудь неподвижную точку А и примем ее за начало отсчета (рис. 2.3).

Д алее, рассматривая траекторию как криволинейную координатную ось, сообщим ей ориентацию, т.е. поло­жительное направление отсчета рас­стояний s = AM. Тогда положение точки М на траектории будет одно­значно определяться криволинейной координатной s , равной расстоянию от точки А до движущейся точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точки М криво­линейная координата s будет изменяться с течением времени, т. е. S = s(t). (8)

Зная уравнение (8), можно определить положение точки в каж­дый момент времени. Уравнение (8) называется уравнением дви­жения, или законом движения вдоль заданной траектории.

Рассмотрим связь между естественным и координатным способами задания движения точки. Для перехода от координат­ного способа задания движения к естественному необходимо:

1. определить уравнение траектории точки,

2. положение точки в начальный момент времени и

3. закон движения точки по ее траектории.

Как определить уравнение траектории, нам уже известно. Для определения положения движущейся точки в начальный мо­мент времени (t = 0) необходимо в уравнения (2) подставить / = 0. Для определения закона движения точки по траектории восполь­зуемся известной из математического анализа формулой длины дуги кривой

(9)

В теоретической механике дифференцирование по вре­мени принято обозначать точкой над дифференцируемой функ­цией. Перепишем формулу (9) в этих обозначениях. s = ± (10)

Знак плюс в формулах (9), (10) берется в том случае, ко­гда точка М движется в сторону с положительного отсчета кри­волинейной координаты Если направление движения точки по траектории изменяется, то знак корня может быть различным для различных интервалов времени. Это изменение знака может быть при колебательном движении точки.

Вопрос № 2

Вывести формулу для определения скорости точки при векторном способе задания её движения

Пусть в некоторый момент времени t положение точки М определяется радиус-вектором r(t), а в момент - радиус-

вектором (рис. 2.4). Тогда перемещение точки М за

промежуток времени

Б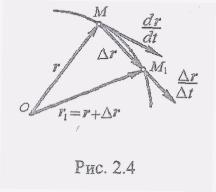 удем считать, что промежуток времени дел.t настолько мал, что с достаточной степенью точно­сти можно предполагать перемещение точки М в положение М1, происходящим равномерно и прямолинейно. В этом слу­чае скорость точки М можно приближен­но вычислить так:

(1)

Для того, чтобы точно вычислить скорость точки в данный мо­мент времени, необходимо в формуле (1) перейти к пределу при стремлении промежутка времени ' к нулю, т.е.

(2)

Этот предел представляет собой первую векторную про­изводную по времени от радиус-вектора точки по времени. Сле­довательно, скорость точки в данный момент времени есть век­торная величина, равная первой производной от радиус-вектора точки по времени

(3)

Как следует из формул (2) и (3), вектор скорости направ­лен по касательной к траектории точки в сторону ее движения.

Вопрос №3

Вывести формулы определения скорости точки при координатном способе задания её движения

Рассмотрим движение точки относительно прямоуголь­ной системы координат (рис. 2.5). В этом случае координаты точ­ки заданы как функции времени:

(1)

Разложим радиус-вектор r по ортам декартовой системы координат:

(2)

З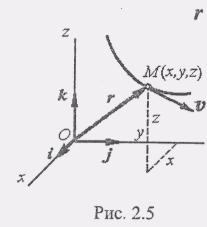 ная, что вектор скорости V равен пер­вой производной от радиус-вектора, продифференцируем равенство (2) по времени. В результате получим разло­жение скорости по ортам i,j, к:

(3)

С другой стороны, разложение вектора скорости V по ортам i,j, k можно представить так:

(4)

где Vх., Vх , Vx –проекции вектора скорости V на оси координат. Сравнивая формулы (3) и (4), находим

(5)

Таким образом, проекции скорости на неподвижные де­картовы оси координат равны первым производным по времени от соответствующих координат движущейся точки.

Из равенства (5) следует, что проекции скорости точки

на координатные оси равны скорости проекции этой точки те же оси. Зная проекции вектора скорости точки V, найдем его мо­дуль:

(6)

Для определения направления вектора скорости восполь­зуемся направляющими косинусами:

(7) где Vx, Vy, Vz, и V определяются равенствами (5) и (6).

Вопрос № 4

Вывести формулу для определения скорости точки при естественном способе задания её движения

Определим скорость точки, предполагая, что ее движе­ние задано естественным способом. Поэтому будем полагать, что известны траектория движения и закон движения точки по траек­тории s = s(t) (рис. 2.6). Каждой точке траектории соответствует определенный радиус-вектор r (t) Так как положение каждой точки траектории определяется дуговой координатой S, то ради­ус-вектор r можно рассматривать как сложную функцию времени t. Тогда

(1) Найдем теперь вектор скорости V точки:

(2)

Известно, что Далее,

так как направлен пределе

(при дел. S-»0) совпадает с касательной к

траектории в точке М, то вектор есть

единичный вектор касательной к траектории (ее орт), направлен­ный в сторону возрастания криволинейной координаты s. Обо­значая орт касательной Т°, запишем формулу (2) в виде

(3)

Эта формула определяет вектор скорости при естествен­ном способе задания движения точки Умножая скалярно обе части равенства (3) на т° и учитывая, что получим

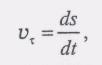(4)

т.е. проекция вектора скорости точки на направление касатель­ной к траектории равна первой производной по времени от кри­волинейной координаты s пo времени. Тогда формулу (3) можно записать так:

(5)

Из формулы(5) следует что модуль скорости V=|Vt|.

Если Vt > 0, то точка движется в положительном направлении отсчета расстояний и VT=V Если же Vт < 0, точка движется в от­рицательном направлении и Vт = — V. Таким образом, модуль век­тора скорости IVI (или V) точки равен модулю ее проекции на направление касательной

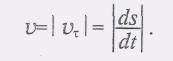(6)

В качестве примера применения формулы (6) рассмотрим скорость точки М при ее движении по окружности радиуса R (рис. 2.7). Скорость точки М в случае ее движения в положительном направлении отсчета расстояний будет иметь численное значение

(7)

так как Величина (8)

называется угловой скоростью вращения радиуса ОМ = R. Таким

образом, при движении по окружности (9)

Направлена скорость по касательной к окружности, следователь­но, перпендикулярно радиусу ОМ.

Вопрос № 5

Вывести формулу для определения ускорения точки при векторном способе задания её движения

Ускорение - физическая величина, характеризующая бы­строту изменения скорости точки во времени.

Пусть точка в момент времени t находится в положении М и имеет скорость V (t), а в момент t1= t + дл.t приходит в поло­жение М1 и имеет скорость V1 (рис. 2.8). Тогда за промежуток времени At = t1— t вектор скорости получает векторное прираще­ние Дл = V1—V, которое определяет изменение вектора скорости и по величине, и по направлению. Для определения приращения скорости дл.V перенесем вектор V1 параллельно своему направле нию в точку М. Далее, соединпе концы векторов V и V1, получим дл.V. Разделив вектор дл.V на соответствующий промежуток време­ни дл.t, получим вектор

(1)

который называется вектором среднего ускорения за промежуток времени t. Вектор среднего уско­рения характеризует особенности движения точки тем точнее, чем меньшему промежутку времени он соответствует. Поэтому естествен­но рассмотреть предел, к которому стремится среднее ускорение, если соответствующий промежу­ток времени At стремится к нулю. Этот предел называют ускорением точки в данный момент времени:

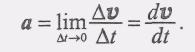(2)

Т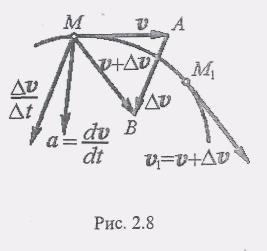 ак как вектор скорости есть первая производная радиус-вектора точки по времени, то

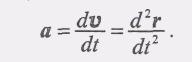(3)

Таким образом, ускорение точки в данный момент вре­мени, есть векторная величина, равная первой производной от вектора скорости или второй производной от радиус-вектора по времени.

Установим теперь положение вектора ускорения а отно­сительно траектории. Отметим, что плоскость треугольника МАВ, образованного векторами V, V1, AV , при At—0) будет поворачи­ваться вокруг вектора V, т.е. вокруг касательной к траектории в точке М, ив пределе займет определенное предельное положе­ние. Это предельное положение плоскости МАВ называется со­прикасающейся плоскостью в точке М траектории. Для плоской кривой эта плоскость есть плоскость самой кривой.

Как видно из рис. 2.8, вектор среднего ускорения аср на­правлен так же, как и AV, т.е. в сторону вогнутости траектории точки, и все время находится в плоскости треугольника МАВ.

Вопрос № 6

Вывести формулы для определения ускорения точки при координатном способе задания её движения

Рассмотрим движение точки М относительно неподвиж­ной прямоугольной декартовой системы координат (см. рис. 2.5). В этом случае ее движение задано следующим образом:

(1)

Разложим радиус-вектор точки по ортам осей Oxyz: (2)

Дифференцируя равенство (2) дважды по времени, полу­чим(3)Или, обозначая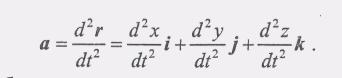 вторые производные по-времени двумя точками, получим разложение ускорения по осям декартовой системы координат в следующем виде: (4) С другой стороны, известно, что (5)Сравнивая равенства (4) и (5), находим формулы для вычисления проекций ускорения на оси декартовой системы координат: (6)Так как Vx= х, Vy= у, Vz= z, то формулы (6) можно пред­ставить еще и так: О)

Т.е. проекции вектора ускорения на неподвижные оси координат равны первым производным по времени от соответ­ствующих проекций вектора скорости или вторым производным от соответствующих координат точки.

По этим проекциям определяем величину и направление вектора ускорения:(8)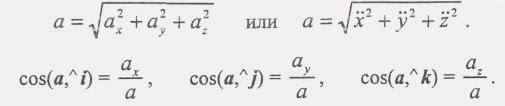 (9)Если во все время движения точка остается в одной плоскости, например в плоскости Оху, то в этом случае во всех формулах нужно положить z = 0.

Вопрос № 7

Дайте определение каждой из осей естественного координатного трехгранника и радиуса кривизны траектории в данной точке

Рассмотрим пространственную кривую. Предельное по­ложение секущей, проходящей через точки М и M1 кривой, когда точка M1 стремится к точке М, называется касательной к кри­вой в данной точке М. Перпендикуляр к касательной в точке М называется нормалью к кривой в этой точке. Геометрическое место нормалей к данной кривой в данной точке называется нормальной плоскостью. Линия пересечения нормальной и сопри­касающейся плоскостей называется главной нормалью. Нормаль, перпендикулярная главной нормали, называется бинормалью.

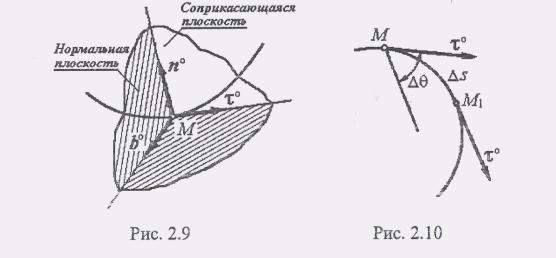
Обозначим единичные векторы: касательной через т°, главной нормали n° и бинормали b°. Через эти векторы проходят плоскости: (т°, n0) - соприкасающаяся, (n0, Ь°) - нормальная и (b°, т°) - спрямляющая. Три взаимно перпендикулярных направ­ления, которые определяются векторами т°, n° и b°, образуют ес­тественную систему координат, или так называемый естествен­ный, или подвижный, трехгранник. Направление т°, n0 и b° определяются так же как направление координатных осей, т.е. по

правой системе, при этом единичный вектор главной нормали всегда направлен в сторону вогнутости кривой (рис. 2.9).

Проведем теперь в двух точках кривой М и М1 единич­ные векторы касательных т° и т1° .Угол между этими касательны­ми называется углом смежности. Обозначим этот угол через дл.8, а длину дуги ММ1 через дл,s (рис. 2.10). Предел отношения дл.8 и дл.s при дл.s-*0, т.е. (1)называется кривизной кривой в данной точке М.

Найдем кривизну окружности радиу­са R. Возьмем на окружности дугу АВ = дл.s и проведем в точках А и В касательные к ок­ружности (рис. 2. 11). Тогда(2)

Отсюда следует, что окружность представляет собой кривую линию постоянной кривизны, равной обратной величине ее радиуса. Кривизна произвольной кривой вообще не­постоянна. Если через три точки М, М1 и М2 кривой провести ок­ружность, то в пределе при приближении точек М1 и M2 к М по­лучим предельную окружность, лежащую в соприкасающейся плоскости, которая называется кругом кривизны (рис. 2.12).

Центркруга кривизны называется центром кривизны, а радиус этого круга - радиусом кривизны кривой в точке М. Вели­чина, обратная кривизне, называется радиусом кривизны данной кривой е данной точке.Обозначая радиус кривизны буквой р, получим

(3)

Как следует из формулы (2), радиус кривизны окружно­сти равен ее радиусу. Очевидно, что кривизна прямой линии рав­на нулю, а ее радиус кривизны равен бесконечности.

Вопрос №8,9 Докажите формулы разложения ускорения по естественным осям координат. 9. Запишите формулы касательного и нормального ускорения точки и проведите их анализ.

Вектор скорости точки можно представить в виде v =vt*t°. (1)

В правой части этого равенства с течением времени изменяются оба множителя: и проекция вектора скорости на касательную v_т, и на­правление единичного вектора t°. Дифференцируя равенство (1) по времени, получим

(2)

dv dv_x d t°

= - t° +vt —

dt dt dt

(3)

Первое слагаемое представляет собой вектор, направленный по касательной. Чтобы определить второе слагаемое, будем рас­сматривать вектор t° как функцию дуговой координаты s. Тогда

d t°

Вектор , входящий в равенство (3), всегда направлен в

ds

сторону вогнутости траектории точки и, как видно из рис. 2.13, лежит в соприкасающейся плоскости. Действительно, приращение вектора t° (см. рис. 2.13) Дл t° = t°1 - t° лежит в плоскости треугольника МАВ. Если

(4)

точка М1 —> М, эта плоскость, вращаясь вокруг неподвижного вектора t°, стремится к предельному положению, т.е. к соприкасающейся плоскости. Далее, дифференцируя тождество t°* t° = 1 по s, получим

а это есть условие перпендикулярности векторов сомножителей.

Т аким образом, рассматриваемый вектор лежит в соприка­сающейся плоскости, направлен в сторону вогнутости траектории и перпендикулярен вектору t°. Следовательно, он направлен по главной нормали к центру кривизны, т.е. по направлению орта п°. Поэтому

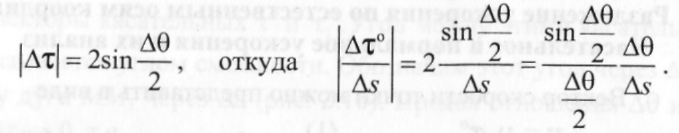
Из треугольника МАВ находим модуль этого вектора

П ереходя в последнем равенстве к пределу при As—>0, найдем поэтому

Тогда окончательно

(6)

Подставляя найденное выражение вектора из (6) в равенство (2) и учитывая что , получим (7)

Формула (7) представляет собой разложение ускорения точки М по ортам естественного трехгранника. Составляющие вектора ускорения по направлениям т° и п° соответственно равны (рис. 2.14)

(8)

П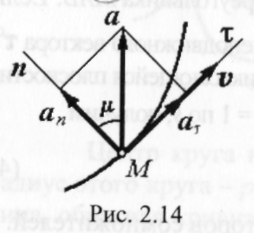 роекция ускорения на направление касательной (9) называется касательным, или тангенциальным ускорением. Проекция ускорения на главную нормаль (10) называется нормальным ускорением.

Т ак как ускорение точки лежит в соприкасающейся плоскости, то проекция ускорения на бинормаль рав­на нулю. Модуль ускорения, на основании формул (9) - (10), будет

Угол между вектором а и главной нормалью можно оп­ределить так:

Анализ формул (9) и (10) показывает, что касательное ускорение характеризует изменение скорости по величине, а нормальное ускорение — изменение скорости по направлению.

Касательное ускорение равно нулю при движении точки с постоянной по модулю скоростью и в моменты времени, когда скорость достигает экстремальных значений. Если vt и аt одного знака, движение называется ускоренным, если же vt и аt разных знаков - замедленным. При аt = 0 движение равномерное.

Нормальное ускорение равно нулю при прямолинейном движении (р = бескон-ть), в точках перегиба криволинейной траектории и в моменты времени, когда скорость точки обращается в нуль.

В заключение отметим, что модули тангенциального и нормального ускорений также можно определить и в случае за­дания движения точки координатным способом.

В самом деле, вспоминая определения модулей скаляр­ного и векторного произведений и представляя единичный вектор

касательной, следующей формулой t°=v/|v|запишем

З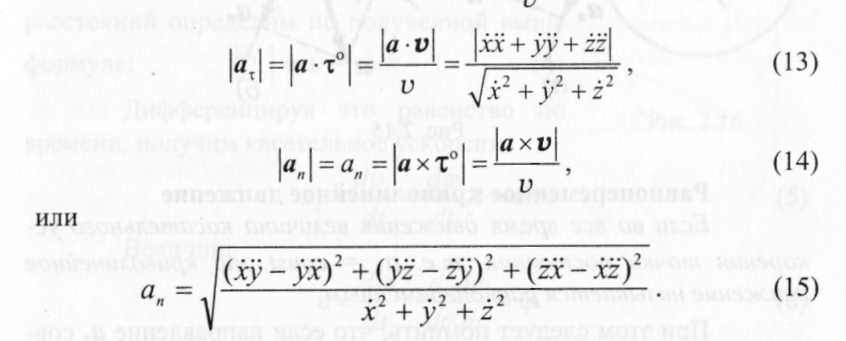 начения этих выражений определяются непосредствен­ным дифференцированием закона движения точки, заданного координатным способом.

Вопрос № 10

Вывести формулы равномерного и равнопеременного криволинейного движения точки. Начертите графики этих движений

Разложение ускорения по естественным осям координат удобно для анализа и классификации различных случаев движе­ния точки.

Равномерное прямолинейное движение. Если во время движения точки ее ускорение равно нулю (а = 0), то такое дви­жение называется равномерным и прямолинейным. Скорость точки в этом случае не изменяется ни по величине, ни по направ­лению.

Прямолинейное переменное движение. Если во время движения точки ее нормальное ускорение равно нулю, то это движение прямолинейное. В самом деле, при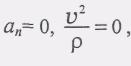 а это значит, что р = ос, т.е. траекторией точки является прямая.

Равномерное криволинейное движение. Если во время движения точки ее тангенциальное ускорение равно нулю (ат=0), то проекция скорости на касательную не изменяется. В этом слу­чае точка движется равномерно по кривой и ее полное ускорение равно нормальному, т.е. а = аn.