8.5. Задачи дробно-линейного программирования

Если целевая функция представляет собой отношение линейных функций, а все условия линейные, то задача относится к классу задач дробно-линейного программирования.

В общем случае целевая функция имеет вид

(8.28)

Такая функция легко преобразуется в линейную, если ее знаменатель при всех допустимых значениях переменных строго положителен. Для этого введем новую переменную r следующим образом

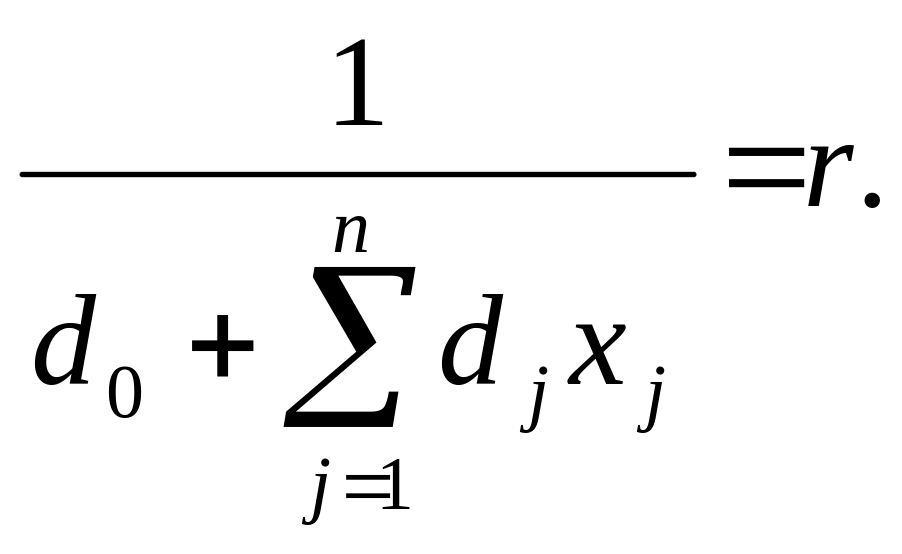(8.29)

Очевидно, что при оговоренном условии она может быть только больше нуля. Тогда функция (8.28) принимает вид

Произведя замену произведения переменных

(8.30) окончательно имеем (8.31)

Получили линейную функцию от n неотрицательных переменных y_j и одной положительной переменной r. Эта функция должна рассматриваться вместе с условием, следующим из (8.29):

или после замены (8.30) (8.32)

Чтобы завершить построение эквивалентной линейной модели, следует ограничения задачи записать в новых переменных. Для этого умножим обе части каждого ограничения

на r:

и, произведя замену, получаем (8.33)

В результате преобразований имеем задачу линейного программирования с критерием (8.31), ограничениями (8.32), (8.33) и переменными r>0, y_j 0, j. Получив ее решение одним из методов ЛП, вычисляем исходные переменные по очевидной формуле

Чтобы гарантировать выполнение условия положительности знаменателя, целесообразно вводить его явно в модель, то есть добавлять неравенство

где  – очень малая положительная константа.

Возможность перехода к линейной задаче геометрически обусловлена тем, что линии уровня дробно-линейной функции описываются линейным уравнением. Действительно, пусть . Тогда из (8.28) следует

или

. (8.34)

Это обычное линейное уравнение относительно x_j. Поэтому линии уровня функции (8.28) в многомерном пространстве – гиперплоскости, а в двухмерном – прямые. Однако с изменением они не перемещаются параллельно, а поворачиваются вокруг множества вращения.

Множество вращения – это множество точек размерности n-2, образованное пересечением нулевых линий уровня числителя и знаменателя:

При n=2 оно состоит из одной точки, а при n=3 представляет собой прямую (ось вращения), образованную пересечением двух плоскостей.

Пример 8.5. Представим графически следующую задачу

;

3x₁ + 2x₂  6,

0 x₁  3,

0 x₂  3.

Уравнения нулевых линий уровня числителя и знаменателя образуют систему

из которой находим точку вращения: x₁=x₂=1/3. На рис. 8.6 это точка А. Нулевые линии показаны пунктиром, а направление поворота, в котором целевая функция возрастает, – стрелками. Отсюда ясно, что оптимальное решение достигается в вершине B:

39. Метод покоординатного спуска и Хука-Дживса Метод первого порядка

Он применим к дифференцируемым функциям в случаях, когда первая производная может вычисляться с высокой точностью.

Рассматриваемый метод средней точки алгоритмически является самым простым из методов одномерной оптимизации на заданном интервале. Он заключается в определении средней точки интервала c=(a+b)/2 и вычислении в ней производной.

Если f '(c) < 0, полагают а = с, при f '(c) > 0, принимают b = с. Условие окончания поиска учитывает точность по координате  и по производной функции ₁:

((b-a)<  )  (| f '(c) | < ₁).

Эффективность метода зависит от трудоемкости вычисления производной. Задаваемая точность ₁ не дожна быть выше точности вычисления производной. С ростом трудоемкости и снижением точности вычислений производной следует отдавать предпочтение прямым методам.

8.7.7. Методы второго порядка

Методы применимы к дважды дифференцируемым функциям. При этом предъявляются высокие требования к точности вычисления производных. Наиболее удачными считаются задачи, в которых известно аналитическое выражение первой производной, а еще лучше – и второй.

Здесь приводится только один из наиболее часто используемых методов – метод Ньютона – Рафсона.

Он основан на линейной аппроксимации первой производной минимизируемой функции f в окрестности текущей точки x_k:

В стационарной точке аппроксимации, которая принимается за очередное приближение x_k+1, производная равна нулю:

.

Отсюда следует рекуррентная формула для построения последовательности приближений к искомому минимуму:

(8.41)

Очевидно, что применение (8.41) возможно только при условии, что для каждого k. Поиск завершается по условию достижения точности, заданной величиной первой производной | f '(x_k) | < ₁ или расстоянием между двумя точками |x_k+1-x_k | < . Возможно одновременное использование этих условий.

В общем случае процедура (8.41) не гарантирует сходимость к стационарной точке. Если начальная точка достаточно близка к стационарной, то метод сходится. При сходимости обеспечивается высокая скорость приближения к минимуму. На рис. 8.14 приведен случай сходимости метода. Очередному приближению соответствует точка пересечения оси x аппроксимирующей прямой. Как видно, последовательность точек x₀,x₁,x₂,… приближается к минимуму x^* .

Д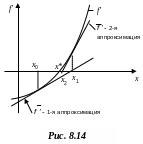 ля некоторых функций результат поиска зависит от выбора начальной точки. Так, например, при начальной точке, взятой правее максимуму производной, так как показано на рис. 8.15, метод расходится.