4. Состязательные задачи. Решение игры 2-х лиц

Этими задачами моделируется принятие решений в ситуациях неопределенности, причем неопределенность обусловлена наличием конфликта. Конфликт имеет место, если в операции участвуют две и более оперирующих сторон, преследующих несовпадающие цели. Неопределенность у одной из сторон возникает в связи с неизвестностью линии поведения других сторон, в то время как результат зависит от поведения всех участников операции.

Различают две модели конфликта: игру и аукционный торг. Игра характеризуется известным количеством участников, называемых игроками, правилами игры, множеством возможных ситуаций (сочетаний стратегий игроков) и соответствующими им выигрышами или проигрышами (в общем случае платежами). По методу ведения игры различают дискретные игры, в которых игроки совершают поочередные ходы, и непрерывные, когда игроки действуют непрерывно. Последние также называют играми преследования (например, бой двух самолетов) или дифференциальными играми, так как поведение игроков описывается дифференциальными уравнениями. По количеству ходов выделяют игры с конечным и бесконечным числом шагов. Аналогичное деление производится по числу стратегий игроков. Так у противотанкового орудия имеется бесконечное число стратегий, так как огонь по нападающим танкам может быть открыт с любого расстояния, начиная с прицельной дальности стрельбы. По форме платы различают игры с нулевой суммой, когда выигрыши одних равны проигрышам других, и поэтому их также называют антагонистическими (цели полностью противоположные), и игры с ненулевой суммой, в которых выигрыши и проигрыши не совпадают. В зависимости от числа игроков говорят об играх . Дискретную игру двух лиц с ненулевой суммой называют биматричной игрой, в ней каждой ситуации соответствует два платежа (по одному для каждого игрока).

Простейшей является дискретная игра двух лиц с нулевой суммой. Такая игра полностью представляется своей платежной матрицей, в которой отражены стратегии игроков и платежи, имеющие противоположный смысл для игроков:

Стратегии игрока	стратегии игрока

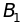
Здесь u_ij - платеж, соответствующий ситуации A_i-B_j. В конкретной игре указывается, что понимается под u_ij. Например, будем дальше считать, что u_ij имеет смысл выигрыша игрока A и, следовательно, для игрока B это проигрыш.

Найти решение такой игры - значит определить оптимальное поведение каждого из игроков и соответствующий результат, называемый ценой игры. Метод решения основан на уже рассматриваемом принципе гарантированного результата, но в отличие от подхода, приведенного в разделе 1.4, он применяется обоими игроками. В данном случае этот принцип означает, что каждый из игроков при выборе своего поведения предполагает наилучшее поведение другого игрока, то есть рассчитывает на наихудший для себя вариант. Таким образом, игрок A будет определять свое поведение на основе максимина , а игрок B - на основе минимакса. Величина называется верхней ценой игры, так как игрок B проиграет не более этой величины, если будет вести себя оптимально, следовательно, - гарантированный проигрыш игрока B, а для игрока A это максимально возможный выигрыш. Нижняя цена игры есть гарантированный выигрыш игрока A, то есть при оптимальном поведении он выиграет не меньше, в то время как для игрока B это минимально возможный проигрыш. Нетрудно доказать, что , и поэтому в общем случае цена игры лежит в диапазоне . Если , то игра имеет решение в области чистых стратегий. Это значит, что каждый из игроков будет придерживаться только одной своей стратегии, иначе говоря, одна (оптимальная) стратегия будет применяться с вероятностью единица, а все остальные - с вероятностью нуль. Такое решение соответствует седловой точке платежной матрицы. Когда u_ij - выигрыш игрока A, в седловой точке значение u_ij^*= и является наибольшим в столбце и наименьшим в строке. Таким образом, при наличии седловой точки решение всегда находится в области чистых стратегий, а оптимальные стратегии - это стратегии, на пересечении которых лежит седловая точка. Для примера приведем платежную матрицу и соответствующее решение, определение которого показано в последнем столбце и последней строке:

	2	3	7	2
	10	2	1	1
	5	4	8	4
	9	1	12	1
	10	4	12

Находя максимум в последнем столбце, получаем нижнюю цену игры 4, а минимум из значений последней строки дает 4. В результате имеем равенство 4, а оптимальными стратегиями являются A₃ и B₂. Нетрудно убедиться, что на их пересечении находится седловая точка платежной матрицы. При таком поведении игрок A гарантирует себе выигрыш не меньше 4, а игрок B проиграет не более 4, и каждому из игроков, как это видно непосредственно из матрицы, невыгодно отклоняться от найденных стратегий.

В тех случаях, когда , решение игры находится в области смешанных стратегий. Это значит, что игроки будут применять более одной стратегии, то есть оптимальное поведение состоит в смешении нескольких стратегий в сочетании, определяемом вероятностями активных стратегий. Следовательно, в результате решения игры должно быть найдено распределение вероятностей на стратегиях каждого из игроков и цена игры.

Проиллюстрируем еще один случай:

	6	8	1	4	1
	5	3	7	6	3
	6	8	7	6

Здесь и, следовательно, , а решение лежит в области смешанных стратегий. Платежная матрица не имеет седловой точки. Если один из игроков имеет только две стратегии, решение можно найти графически. Для этого проводятся две оси ординат на расстоянии, которое принимается за единицу. На этих осях откладываются платежи игрока, имеющего две стратегии. В нашем примере стратегиям A₁ и A₂, соответствуют оси ординат на которых откладываются выигрыши игрока A. Зафиксируем стратегию B₁. Тогда игрок А выиграет 6 при выборе стратегии (в этом случае вероятность применения этой стратегии равна 1) и выиграет 5, когда будет применять только стратегию A₂ (теперь вероятность применения этой стратегии равна 1). 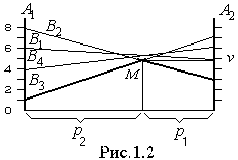Если же применять стратегию A₁ с вероятностью , а стратегию A₂ с вероятностью , то ожидаемый выигрыш составит 6x₁+5(1-x₁)=5+x₁. Значит, выигрыш зависит от вероятности линейно, что и показано на рис.1.2.

Аналогично строятся прямые, соответствующие выигрышам игрока А при фиксации других стратегий игрока B. Гарантированные выигрыши игрока A лежат на нижней грани, выделенной жирной линией. Очевидно, что игрок стремится к максимальному гарантированному выигрышу, который достигается в точке M. Следовательно, оптимальное решение для игрока A состоит в применении стратегии A₁ с вероятностью и стратегии A₂ с вероятностью . При этом цена игры равна 49/11. Обратим внимание на отсчет вероятностей: растет от 0 до 1 справа налево, а - наоборот, и значения вероятностей определяются как доли расстояния между осями координат. Теперь можно найти решение и для игрока B. Его активные стратегии (вероятности которых больше 0) определяются точкой M - это стратегии B₂ и B₃. Вероятности применения этих стратегий находятся с помощью графика, аналогичного приведенному на рис.1.2, но оси ординат должны соответствовать B₂ и B₃. Они могут быть вычислены и аналитически. Отметим, что оптимальное решение в области смешанных стратегий может быть реализовано только при многократном (теоретически бесконечном) повторении игры, а цена игры есть соответствующее оптимальному поведению математическое ожидание результата (средний выигрыш или проигрыш на один розыгрыш).

Иногда можно сократить число стратегий одного из игроков или даже обоих за счет отбрасывания доминируемых стратегий, то есть стратегий, которые заведомо не будут активными в оптимальном решении. Для выявления таких стратегий проводят попарные сравнения стратегий одного из игроков. Та стратегия, на которой платежи не лучше, чем на другой, для всех стратегий противника и хотя бы для одной хуже, является доминируемой и может быть отброшена. После сокращения числа стратегий у одного игрока возможно появление доминируемых стратегий у второго. Поэтому анализ можно повторять, поочередно меняя игрока, пока не удалятся все доминируемые стратегии. Если число стратегий у одного из игроков сократится до двух, игра решается графически. В общем случае решение в области смешанных стратегий находится методами линейного программирования.

Помимо рассмотренных применяются также модели коалиционных и кооперативных игр. Так, в игре лиц ( 2) с нулевой суммой в процессе игры могут образовываться объединения части игроков против остальных, если такая коалиция улучшает результаты всех объединившихся игроков, что обеспечивается побочными платежами со стороны инициатора объединения. В отличие от этого кооперативная игра может улучшать результаты всех игроков за счет предварительных договоренностей с заключением обязывающих соглашений (в играх с ненулевой суммой). Очевидно, что кооперация возможна и в игре двух лиц.

Одним из классов бескоалиционных игр являются позиционные игры. Они моделируют процессы последовательного принятия решений. Игра состоит в переходе из одного состояния игры в другое , происходящем при каждом выборе действия одним из игроков или случайным образом. Последовательные состояния и называют позициями. Выбор игрока может происходить при полной и неполной информации о его позиции. Примерами таких игр являются шахматы, шашки, домино и др. Позиционная игра может быть нормализована, то есть сведена к матричной игре.

Игровые модели находят применение в основном при исследовании военных операций и в экономике. Если вторая оперирующая сторона представляет собой некую среду с неизвестными вероятностями состояний, то такая ситуация также может моделироваться игрой, которая называется игрой против природы.

Модели типа аукционного торга применяются, когда степень неопределенности выше, чем предполагает модель игры. Так, например, в аукционном торге неизвестно даже число участников, нельзя составить принятую в игре платежную матрицу. Разработка и исследование моделей этого типа находятся в начальной стадии.