Множественная линейная регрессионная модель в натуральном масштабе. Множественная регрессия широко исп-ся в решении проблем спроса, доходности акций, издержек пр-ва и других вопросах. Основная цель МР- построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также их совокупное воздействие на моделируемый показатель.

yх=a+b₁x₁+b₂x₂+e. – характеризует связи м/у результативной переменной - у, и несколькими независимыми переменными – х.

ух - расчетное значение результативного признака,

х - факторные признаки,

b – неизвестные параметры.

При построении учитываются следующие условия Гаусса-Маркова:

1. М(Ei)=0

2. D(Ei)=const

3. Случайные ошибки модели регрессии не коррелируют м/у собой, т.е. Cov(Ei)2набл.=0

4. Случайные ошибки – случайная величина, подчиняющаяся нормальному закону распределения, т.е. с «0» М и D.

Уравнение множественной линейной регрессии в стандартизованном масштабе. Означает, что все переменные включаются в модель регрессии стандартизовано, с помощью специальных формул.

На основе матрицы парных коэф-тов корреляции строится ур-е регрессии в стандартизованном масштабе:

t_y = B1*t_x1 + B2*t_x2 + B3*t_x3 + E,

Где t – стандартизованные переменные, B – стандартизованные коэф-ты регрессии.

Применяя МНК к ур-ю множеств регрессии в стандартизов-ом масштабе, после преобразований получим систему вида

r_y,x1 = B1 + B2*r_x1,x2 + B3*r_x1,x3

r_y,x2 = B1*r_x2,x1 + B2 + B3*r_x2,x3

r_y,x3 = B1*r_x3,x1 + B2*r_x3,x2 + B3

Из этой системы можно найти коэф-ты B . Они показ-ют на сколько единиц изменится в среднем рез-тат, если соотв-щий фактор xi изменится на одну единицу при неизменном среднем уровне других факторов. В силу того, что все перем-ые B сравнимы между собой (в отличие от коэф-тов «чистой» регрессии), после этого сравнения можно ранжировать факторы по силе их воздействия на результат.

Частные коэффициенты корреляции.

Частные коэффициенты (индексы) корреляции характеризуют тесноту связи между двумя признаками при исключении влияния третьего признака. Эти показатели представляют собой отношение сокращения остаточной дисперсии за счет включения доп. факторов. Если рассматриваемая регрессия с числом факторов Р, то возможны коэффициенты корреляции первого, второго и т.д. Р-1 порядков, т.е.

ryx1.x2= корень квадр из(1-(1-R²yx1x2)/(1-r²yx2),

ryx2.x1= корень квадр из(1-(1-R²yx1x2)/(1-r²yx1).

Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается.

Коэффициенты множественной корреляции, свойства коэффициента.

Показатели множественной корреляции характеризуют тесноту связи, рассматриваемого набора фактора с исследуемым признаком, т.е. оценивает тесноту связи совместного влияния фактора на результат.

, r – номера признака, связь м/у которыми оценивается этим коэф-ом корреляции.

Свойства:

1. Изменяется в пределах [0;1],не используется для определения направленности связи.

2. Чем ближе к 1, тем теснее связь результативного признака со всем набором исследуемых факторов; Если значение близко к 0, то взаимосвязь слабая.

3. Величина коэф-та множественной корреляции должна быть ≥ максимальному парному индексу корреляции.

4. Добавление в уравнение множественной регрессии новую факторную переменную увеличивает значение множественного коэффициента корреляции.

Оценка параметров уравнения множественной регрессии (Дисперсионный анализ).

Оценка значимости уравнения регрессии в целом дается с помощью критерия Фишера.

Перед расчетом критерия проводится дисперсионный анализ.

1.Выдвигаем нулевую гипотезу о статистической незначимости коэффициента регрессии и, следовательно, уравнения в целом: .

2.Строим схему дисперсионного анализа. Рассчитываем среднеквадратическое отклонение (СКО):

;

;

.

3.Определяем наблюдаемое значения F- критерия:

.

Определяем табличное значение F- критерия:

4.Сопоставляем наблюдаемое и табличное значение, записываем вывод:

F_факт > F_табл , то нулевая гипотеза отклоняется и делается вывод о том, что уравнение регрессии статистически значимо.

F_факт < F_табл, то нулевая гипотеза не отклоняется и делается вывод о том, что уравнение регрессии статистически незначимо.

Частный f-критерий Фишера.

С помощью F-критерия Фишера опред-ся значимость уравнения множеств регрессии в целом. Позволяет оценить целесообразность включения в уравнение множественной регрессии фактора х1 после х2, х2 после х1.

;

R²yx_1...xm-коэффициент множественной детерминации для регрессии с полным набором факторов.

R²yx_1...x_i-1; x_i+1...x_m-для ур-ия множеств-й регрессии без включения в модель фактора x_i. Частный F критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом.

Если Fxi>Fтабл при α=0,05 (заданном), то включение xi-го фактора статистически оправдано.

Если Fxi<Fтабл – то не оправдано.

С помощью частного F-критерия можно проверить значимость всех коэф-ов регрессии, предлагая, что каждый соотв-щий фактор x_i вводился в ур-ие множ-й регр последним.

Оценка параметров уравнения множественной регрессии (по t-критерию Стьюдента).

1.Выдвигаем нулевую гипотезу о статистической незначимости коэффициентов чистой регрессии: .

2.Наблюдаемое значение критерия:

.

3.Стандартная ошибка коэффициента:

.

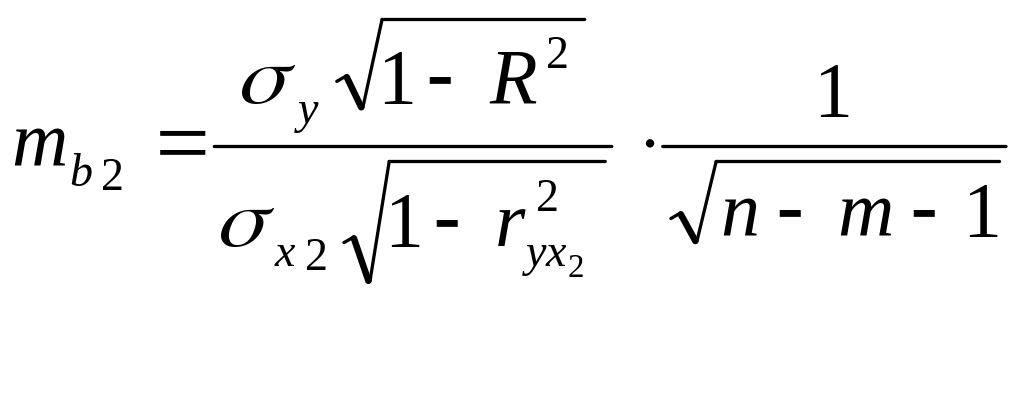4.Табличное значение t- критерия, .

5. Сопоставляем наблюдаемое и табличное значение, записываем вывод:

и > t_табл, то нулевая гипотеза отклоняется и делается вывод о том, что коэффициенты уравнения статистически значимы.

и < t_табл, то нулевая гипотеза принимается и делается вывод о том, что коэффициенты уравнения статистически незначимы.

Отбор факторов при построении уравнения множественной регрессии.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

• Метод исключения (обратный метод) – отсев факторов из полного его набора признака ставшие незначимы по t-критерию Стьюдента.

• Метод включения (прямой метод) – дополнительное введение фактора.

• Шаговый регрессионный анализ – исключение ранее введенного фактора (проверка значимости).

Нелинейная регрессия. Классификация нелинейных регрессий.

Примерами нелинейных моделей служат:

-производственная функция (зависимость м/у объёмами производства и основными факторами производства).

- функция спроса.

IIкласса:

1. регрессии, нелинейные относительно включенных в анализ факторных переменных, но линейные по оценке коэффициентов;

2. регрессии, нелинейные по оцениваемым коэффициентам.

1класс, модели:

• Полиномы 1-го порядка, т.е. процесс с монотонным развитием (не предела роста);

• Полиномы 2-го порядка, т.е. равноускоренное развитие процесса (рост или снижение);

• Гипербола:

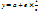
Гиперболической фун-й является кривая Филипса. Закономерность: с ростом доходов, доля доходов расходуемых на продовольствия уменьшается, а доля доходов расходуемых на непроизводственные товары увеличивается.

Для 1-го класса нелинейных моделей метод МНК применяется путём замены факторной переменной: 1/х=z, y=a+b+z.

Особенность нелинейных моделей первого класса в том, что в результате преобразований модели могут быть приведены к линейному виду, поэтому к ним можно будет применить классический МНК.

2класс, модели:

• Степенная (кривая спроса и предложения, производственная функция);

• Показательная

• Экспоненциональная

• Логарифмическая (кривая насыщения), используется для описания процессов которые имеют предел роста (демография и т.д.).

Второй класс разделяют на два типа:

1. Если нелинейную модель по оцениваемым параметрам можно привести к линейному виду, то она будет называться нелинейная модель внутренне линейная (степенная ).

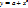2. Если модель нельзя привести к линейному виду, то её называют нелинейная модель внутренне нелинейная.

Корреляция и детерминация для нелинейной регрессии.

Оценка параметров осуществляется для 1-го класса нелинейных моделей (аналогично парной и множественной регрессии).

Показатель корреляции - индекс корреляции.

Индекс корреляции используется для выявления тесноты связи между переменными в случае нелинейной зависимости.

Свойства индекса корреляции:

1. Находится в интервале от 0 до 1 включительно;

2. Значимость проверяется F-критерием Стьюдента, аналогично парной регрессии.

Показатель детерминации для нелинейных моделей называется индексом детерминации.

F-критерий Фишера для нелинейной регрессии.

Выдвигаем нулевую гипотезу: - о статистической не значимости индекса детерминации и следовательно уравнения в целом.

Наблюдаемое значение F – критерия, определяется по формуле:

Табличное значение F- критерии:

Вывод: так как Fнабл>Fтабл., отклоняется и, следовательно, уравнение нелинейной регрессии в целом также признается статистически значимым.

Fнабл<Fтабл., не отклоняется и, следовательно, уравнение нелинейной регрессии в целом также признается статистически не значимым.

Коэффициент эластичности для разных видов МНК.

Коэффициент эластичности для нелинейных моделей характеризует, на сколько процентов измениться в среднем результат, если, если факторные переменные изменятся на 1%.

Вид функции	Коэффициент эластичности
Парабола второго порядка
Гипербола
Показательная
Степенная	в

Предпосылки МНК: гомо и гетероскедастичности.

Условия необходимые для получения свойств оценок уравнения регрессии:

1. Случайный характер остатка. Для определения данной предпосылки строится график зависимости остатков от расчётных значений результативных переменных, если график остатков образует горизонтальную линию, то предпосылка считается оправданной.

2. Нулевая средняя величина остатка независящая от переменной X. Для определения строится график зависимости остатков, но по оси X будет обозначаться факторная переменная. Данное условие будет выполняться для линейных моделей и нелинейных относительно включённых в них переменных.

Если график значений также образует горизонтальную линию, то остатки будут независимы от переменной X.

Если будет формироваться, какая либо зависимость то данная предпосылка невыполнима.

3. Гомоскедастичность (а=в=с): определение, графическое изображение, последствия гетероскедастичности, и методы определения гетероскедастичности.

Дисперсия остатков постоянна, это означает, что для каждого значения фактора X остатки имеют одинаковую дисперсию, если эта предпосылка не выполняется, то имеет место гетероскедастичности(а>в>с).

Последствия гетероскедастичности остатка:

1. Для оценок регрессии не выполняется условие эффективности.

2. Появляется возможность неверного вычисления стандартных ошибок коэффициентов.

4)Отсутствие автокорреляции остатков.

Автокорреляция - корреляция между остатками текущего и предыдущего значения. Автокорреляция определяется критерием Дарбина-Уотсона.

Если эти предпосылки не соблюдаются необходимо:

1. Проектировать модель, то есть изменить её спецификацию.

2. Изменить состав факторной переменной,

3. Преобразовать исходные данные.