
- •Введение
- •Формирование алфавитов классов и признаковых пространств радиолокационного распознавания
- •1.1. Общие сведения
- •1.2. Формирование алфавитов классов
- •1.3. Траекторные признаки
- •1.4. Сигнальные признаки однопозиционной активной локации при узкополосном зондировании
- •1.4.1. Эффективные площади (эп) целей
- •Примерные эффективные площади радиолокационных целей
- •1.4.2. Поляризационные признаки
- •1.4.3. Модуляционные признаки
- •1.5. Сигнальные признаки однопозиционной активной локации при широкополосном, многочастотном и многодиапазонном зондировании
- •1.5.1. Признаки при широкополосном зондировании
- •Скалярные признаки подклассов целей
- •Дальностно-поляризационные портреты (дпп)
- •О переходе от согласованного дальностного разрешения к сверхразрешению
- •Дальностно-частотные портреты (дчп)
- •Дальностно-угловые портреты (дул)
- •1.5.2. Признаки при многочастотном зондировании
- •Признаки при когерентном зондировании сигналами малой протяженности
- •Признаки при когерентном зондировании сигналами большой протяженности.
- •Признаки при некогерентном многочастотном зондировании
- •1.3.3. Признаки при многодиапазонном зондировании
- •1.6. Сигнальные признаки однопозиционной пассивной локации
- •1.7. Сигнальные признаки многопозиционной активно-пассивной локации
- •1.8. Признаковые пространства распознавания
- •1.9. Эффективность радиолокационного распознавания
- •2. Алгоритмы распознавания по совокупности признаков
- •2.1. Общие сведения
- •2.2. Байесовские одноэтапные алгоритмы распознавания
- •2.2.1. Исходные структуры алгоритмов
- •При этом отношение
- •2.2.2. Мультипликативные байесовские алгоритмы и их частичная
- •2.2.3 Аддитивные частично параметризованные байесовские алгоритмы
- •2.2.4. Примеры элементов байесовских алгоритмов
- •Элементы алгоритмов, связанные с измерением эффективных площадей целей
- •Элементы алгоритмов связанные с получением дальностных портретов целей
- •2.3. Непараметрические алгоритмы многоальтернативного распознавания
- •2.3.1. Алгоритмы вычисления расстояний
- •2.3.2. Алгоритмы голосования
- •2.4. Нейрокомпьютерные алгоритмы
- •2.4.1. Принципы построения и структуры и ейро компьютерных алгоритмов
- •2.4.2. Варианты алгоритмов функционирования и обучения
- •2.4.3. Нейробайесовские алгоритмы
- •2.4.4. Некоторые данные моделирования
- •3. Принципы реализации высокого разрешения по дальности и по угловой координате в одпопозиционных системах радиолокационного распознавания
- •3.1. Общие сведения
- •3.2. Возможности и примеры получения дальностных портретов
- •3.2.1. Методы когерентной обработки сигналов
- •3.2.2. Примеры когерентной обработки сигналов
- •3.3. Принципы реализации высокого разрешения за счет прямого синтеза апертуры
- •3.4. Пример синтеза апертуры на спутнике "Сисат", сша, 1978 [41]
- •3.5. Обратный (инверсный) синтез апертуры и формирование дальностно-угловых портретов
- •3.6. Варианты адаптации к случайным параметрам сигналов
- •3.7. Адаптация к неравномерному движению цели без угловых рысканий
- •3.8. Принципы адаптации к рысканиям цели
- •3.8.1. Применение методов углового сверхразрешения
- •3.8.2. Сочетание когерентной обработки с некогерентной
- •3.8.3. Компенсация амплитудно-фазовых флюктуаций, обусловленных
- •4. Экспериментальные и расчетные методы определения характеристик вторичного излучения и показателей качества радиолокационного распознавания
- •4.1. Общие сведения
- •4.2. Экспериментальные методы определения характеристик вторичного излучения
- •4.2.1. Методы натурных измерений
- •4.2.2. Методы масштабного электродинамического моделирования
- •4.2.3. Методы гидроакустического моделирования
- •4.3. Расчетные методы определения характеристик вторичного излучения
- •4.3.1. Разновидности расчетных методов
- •4.3.3. Динамические цифровые модели вторичного излучения
- •Варианты построения динамических моделей
- •4.4. Методы определения показателей качества радиолокационного распознавания
- •4.4.1. Натурные методы
- •4.4.2. Методы физического моделирования
- •4.4.3. Методы математического моделирования
- •4.4. Примеры математического моделирования распознавания воздушных целей по совокупности признаков
2.2.3 Аддитивные частично параметризованные байесовские алгоритмы
Переход от мультипликативных алгоритмов к аддитивным основан на монотонности логарифмической функции. Логарифм произведения в квадратных скобках (2.12) достигает максимума одновременно с самим этим произведением. Он сводится при этом к сумке логарифмов сомножителей, что упрощает вычисления. Отсюда приходим к частично параметризованным аддитивным алгоритмам распознавания
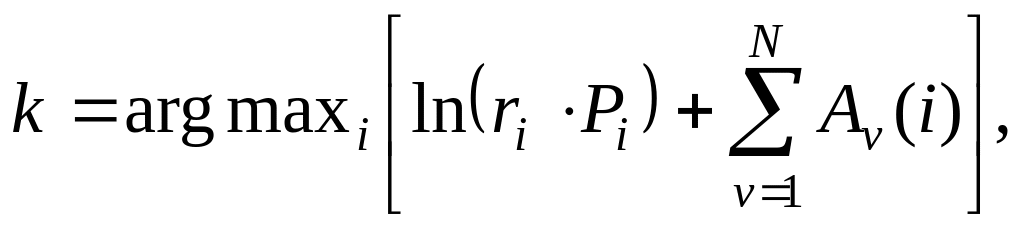 (2.13)
(2.13)
где
![]() - неоднородные слагаемые.
- неоднородные слагаемые.
![]() (1.4)
(1.4)
Аддитивные алгоритмы, наряду с мультипликативными, применимы не только при независимости подреализаций yv, но и при независимости ошибок измерений параметров по одной и той же реализации или подреализации.
2.2.4. Примеры элементов байесовских алгоритмов
Элементы алгоритмов, связанные с измерением траекторных параметров объектов в тропосфере
Маневренность
тропосферных объектов, большая по
сравнению с космическими объектами,
сужает совокупность признаков
распознавания. Входящие в (2.13) - (2.14)
априорные распределения параметров
![]() (с учетом ошибок измерения) приходится
задавать описаниями общего вида.
Последние могут относиться к
одномерным и многомерным, односвязным
и многосвязным, ступенчатым и непрерывным,
негауссовским и гауссовским распределениям.
(с учетом ошибок измерения) приходится
задавать описаниями общего вида.
Последние могут относиться к
одномерным и многомерным, односвязным
и многосвязным, ступенчатым и непрерывным,
негауссовским и гауссовским распределениям.
Обобщая распределение вектор-столбца скоростей и высот цели на плоскости v - Н (рис. 1.1), введем многомерные односвязные ступенчатые негауссовское распределение и распределение его логарифма, равномерные в пределах области, заданной линейными ограничениями,
![]() (2.15)
(2.15)
Здесь
![]() – вектор-столбец размера
– вектор-столбец размера
![]() ,
Вi
– вектор-столбец размера
,
Вi
– вектор-столбец размера
![]() .
Аi
- матрица размера
.
Аi
- матрица размера
![]() ,
пi
-
число ограничений на скалярные параметры
вектора
.
Значение
,
пi
-
число ограничений на скалярные параметры
вектора
.
Значение
![]() –
объем многогранника, определяемого
ограничениями. Выполнение приведенных
матричных неравенств понимается в
смысле выполнения всех скалярных
неравенств, на которые они распадаются.
При переходе от односвязных распределений
к многосвязным ограничения (2.15) и
величины рi
для каждой из односвязных подобластей
подбираются раздельно.
–
объем многогранника, определяемого
ограничениями. Выполнение приведенных
матричных неравенств понимается в
смысле выполнения всех скалярных
неравенств, на которые они распадаются.
При переходе от односвязных распределений
к многосвязным ограничения (2.15) и
величины рi
для каждой из односвязных подобластей
подбираются раздельно.
Примером одномерного, непрерывного негауссовского распределения является обобщение гауссовского:
![]() (2.16)
(2.16)
Здесь
ai
– условное (для целей i-го
класса) математическое ожидание
параметра а: γi
–
полуширина распределения на уровне
![]() μ – характеристика формы распределения.
Кривая – гауссовская при μ=1, двусторонняя
экспоненциальная при μ=1/2 и приближается
к прямоугольной с увеличением μ при
μ – характеристика формы распределения.
Кривая – гауссовская при μ=1, двусторонняя
экспоненциальная при μ=1/2 и приближается
к прямоугольной с увеличением μ при
![]() .
Нормирующий множитель Qi
выражается через гамма-функцию:
.
Нормирующий множитель Qi
выражается через гамма-функцию:
![]() (2.17)
(2.17)
Примером
непрерывного трехмерного односвязного
распределения для а= \уНа\,
где а
-
полное ускорение, является распределение
![]() вида
вида
 (2.18)
(2.18)
Трехмерное распределение (2.18) предполагает независимость априорных одномерных распределений v, Н, а в. Вводя в (2.18) слагаемые в виде степеней линейных комбинаций величия v, Н, а, можно учесть взаимную зависимость распределений этих величин.
