
- •Вместо введения: о погрешностях при решении прикладных задач
- •Глава I. Численные методы решения уравнений
- •§ 1. Задача локализации корней
- •Ограничение корней
- •Локализация корней
- •Простейший (грубейший) алгоритм локализации корней:
- •§ 2. Понятие об итерационных методах уточнения корней
- •Метод деления пополам (метод вилки)
- •§ 3. Методы хорд и касательных
- •Метод хорд для монотонных выпукло-вогнутых функций
- •Метод касательных для монотонных выпукло-вогнутых функций
- •§ 4. Метрические и банаховы пространства. Теорема о неподвижной точке
- •Матричные нормы
- •§ 5. Метод простой итерации
- •§ 6. Применение метода простой итерации к решению
- •Условие h([; ]) [; ] :
- •Глава II. Вычисления в линейной алгебре
- •§ 1. Метод Гаусса и его улучшения для повышения точности решения
- •§ 2. Метод простой итерации и метод Зейделя
- •§ 3. Подготовка к применению метода простой итерации
- •§ 4. Проблема собственных значений
- •Глава III. Численное интегрирование
- •§ 1. Метод прямоугольников
- •§ 2. Метод трапеций
- •§ 3. Метод Симпсона (параболическое интерполирование)
- •Глава IV. Некоторые методы аппроксимации функций
- •§ 1. Интерполяционный многочлен Лагранжа
- •§ 2. Интерполяционный многочлен Ньютона
- •§ 3. Метод наименьших квадратов
- •Глава V. Некоторые методы численного решения дифференциальных уравнений
- •Приложение: Сводка характеристик численных методов
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
§ 4. Проблема собственных значений
TO BE ADDED…
Глава III. Численное интегрирование
З адача
численного интегрирования состоит в
приближённом вычислении с заданной
точностью определённого интеграла
адача
численного интегрирования состоит в
приближённом вычислении с заданной
точностью определённого интеграла
![]() для непрерывной на отрезке [a;
b]
функции.
Здесь интеграл понимается как предел
интегральных сумм
для непрерывной на отрезке [a;
b]
функции.
Здесь интеграл понимается как предел
интегральных сумм
![]() , где участвует любое разбиение a
= x0
< x1
< … < < xn–1
< xn
= b
отрезка [a;
b]
на n
отрезков
[xi
; xi+1]
длин i
= xi+1
– xi
, в каждом
из которых фиксирована точка i
[xi
; xi+1]
(0
i
n–1).
Этот предел рассматривается при
стремлении к нулю величины
=
, где участвует любое разбиение a
= x0
< x1
< … < < xn–1
< xn
= b
отрезка [a;
b]
на n
отрезков
[xi
; xi+1]
длин i
= xi+1
– xi
, в каждом
из которых фиксирована точка i
[xi
; xi+1]
(0
i
n–1).
Этот предел рассматривается при
стремлении к нулю величины
=
![]() i
(что,
конечно, предполагает n
) и не должен
зависеть ни от разбиения a
= x0
< x1
<…< xn–1
< xn
= b,
ни от выбора точек i
[xi
; xi+1]
(1
i
n–1)
– только в этом случае интеграл и
считается корректно определённым.
i
(что,
конечно, предполагает n
) и не должен
зависеть ни от разбиения a
= x0
< x1
<…< xn–1
< xn
= b,
ни от выбора точек i
[xi
; xi+1]
(1
i
n–1)
– только в этом случае интеграл и
считается корректно определённым.
В этой главе рассматриваются некоторые методы решения поставленной задачи численного интегрирования.
§ 1. Метод прямоугольников
Э тот
метод предполагает равномерное разбиение
отрезка [a;
b]
на n
равных
частей длины i
=
с выбором
точек i
в серединах
интервалов [xi
; xi+1]:
i
=
тот
метод предполагает равномерное разбиение
отрезка [a;
b]
на n
равных
частей длины i
=
с выбором
точек i
в серединах
интервалов [xi
; xi+1]:
i
=
![]() (0
i
n–1).
(0
i
n–1).
Если обозначить f(i) = fi+1/2 , то заменив интеграл n-й интегральной суммой, получим формулу прямоугольников:
![]() .
.
Её название связано с прямоугольниками, т.к. она заменяет значение интеграла суммой площадей n прямоугольников с одним основанием и высотами f1/2 , … , fn–1/2 (см. рисунок).
Для того чтобы осмысленно применять эту формулу, нужно оценить погрешность, с которой она даёт значение интеграла. Предположим, что функция f дважды непрерывно дифференцируема на [a; b]. Тогда на каждом интервале [xi ; xi+1] можно воспользоваться формулой Тейлора:
f(x) =
f(i)
+ f(i)·(x
– i)
+
![]() ·(x
– i)2
,
·(x
– i)2
,
где лежит между x и i и зависит от x. Интегрируя по x в отрезке [xi ; xi+1], получим
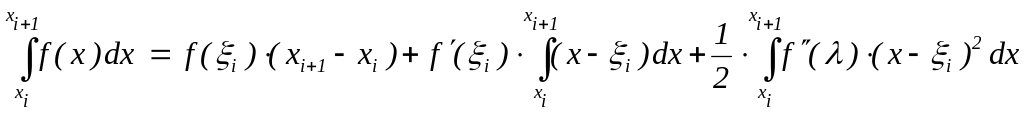 ,
,
причём среднее слагаемое в правой части равно нулю:
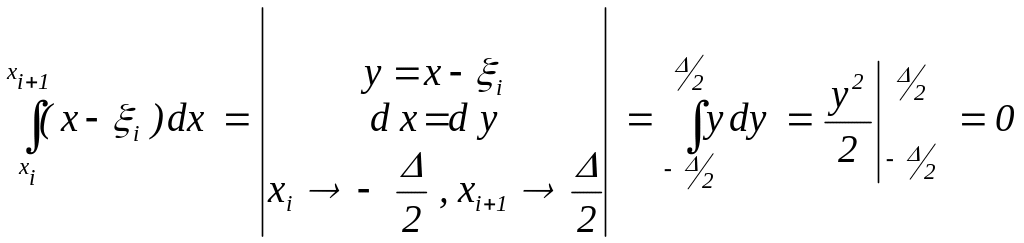 ,
,
где
= xi+1
– xi
. Значит,
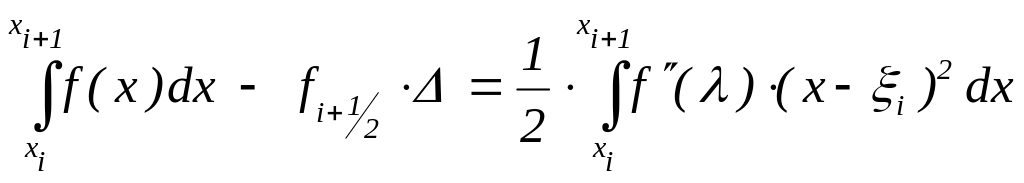 ,
причём
,
причём
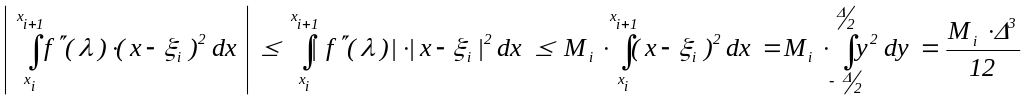 ,
,
где Mi = max{|f(x)| | xi x xi+1 }.
Таким образом,
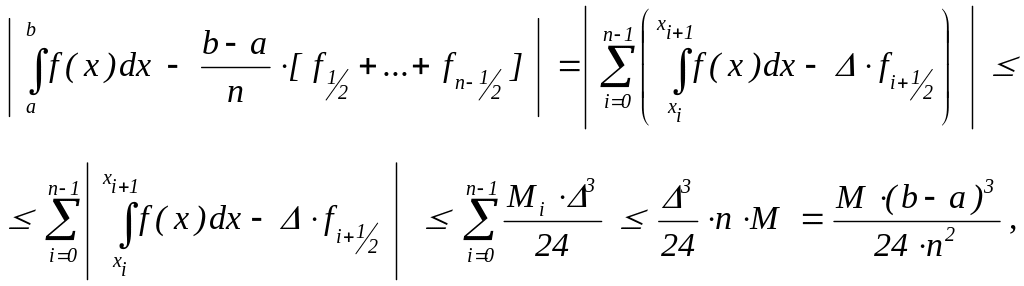
где M
=
![]() |f(x)|
.
|f(x)|
.
Полученная оценка
позволяет по заданной погрешности
из неравенства
![]() находить число n
: n
>
находить число n
: n
>
![]() и
=
, а затем
применять формулу прямоугольников
и
=
, а затем
применять формулу прямоугольников
![]() .
.
Пример. Вычислить
с точностью до 0,001
интеграл
![]() .
.
Оцениваем вторую производную подынтегральной функции:
![]() ,
,
т.к.
3·x2
– 1
3·12
– 1 = 2,
![]() .
.
Вычисляем n
>
![]() ,
т.е. n
= 13.
Теперь
пользуемся методом прямоугольников:
,
т.е. n
= 13.
Теперь
пользуемся методом прямоугольников:
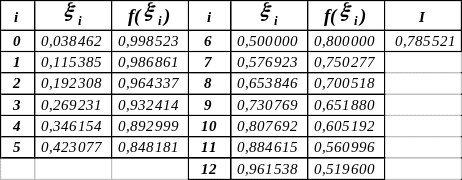
Сравнивая полученное
значение интеграла с точным значением
![]()
0,785398, получим
0,785398, получим
|![]() – I
|
|0,785398 – 0,785521|
0,000123 < 0,001,
– I
|
|0,785398 – 0,785521|
0,000123 < 0,001,
что и требовалось.
§ 2. Метод трапеций
Разобьём отрезок [a; b] на n равных частей длины = и впишем в подграфик функции f прямоугольные трапеции, как показано на рисунке. Если обозначить f(xi) = fi , то заменив интеграл, численно равный площади подграфика, суммой площадей трапеций, получим формулу трапеций:
![]() .
.
И з
рисунка видно, что на отрезках, где
функция меняет знак, вместо трапеции
получаются два треугольника.
з
рисунка видно, что на отрезках, где
функция меняет знак, вместо трапеции
получаются два треугольника.
Для того чтобы
осознанно пользоваться этой формулой,
нужно оценить погрешность, с которой
она даёт значение интеграла. Предположим,
что функция f
дважды
непрерывно дифференцируема на [a;
b].
Тогда на каждом интервале [xi
; xi+1]
она заменяется
линейной функцией
![]() .
Оценим разность
.
Оценим разность
r(x) = f(x) – L(x) – K·(x – xi)·(x – xi+1),
где x
(xi
; xi+1),
а K
– постоянная
со свойством r(y)
= 0 для
некоторой фиксированной точки y
(xi
; xi+1),
т.е. K
=
![]() . Таким
образом, дважды непрерывно дифференцируемая
функция r(x)
обращается
в ноль, по крайней мере, в трёх точках:
xi
, y,
xi+1
.
. Таким
образом, дважды непрерывно дифференцируемая
функция r(x)
обращается
в ноль, по крайней мере, в трёх точках:
xi
, y,
xi+1
.
По теореме Роля,
производная r(x)
имеет, по
крайней мере, по одному корню на каждом
их отрезков (xi
; y)
и (y
; xi+1).
Ещё раз применяя теорему Ролля, получим,
что у второй производной r(x)
есть корень
на (xi
; xi+1).
С другой стороны, r(x)
= f(x)
– 0 – 2·K.
Таким образом, K
=
![]() , где
(xi
; xi+1)
– корень
r(x).
Итак,
, где
(xi
; xi+1)
– корень
r(x).
Итак,
f(y) = L(y) + ·(y – xi)·(y – xi+1),
т.к. r(y) = 0, а зависит от y.
Интегрируя по y в отрезке [xi ; xi+1], получим
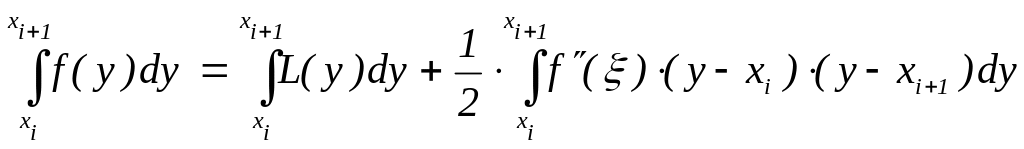 ,
,
причём первое слагаемое в правой части равно:
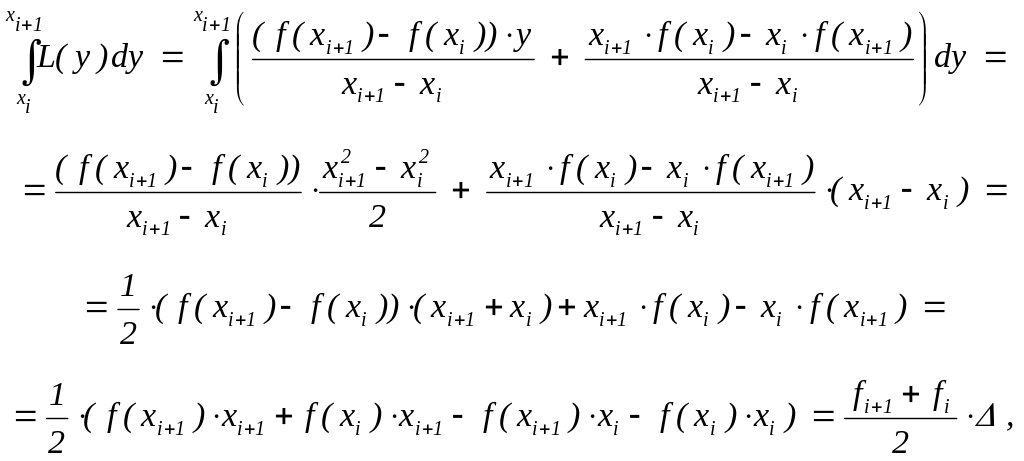
где
= xi+1
– xi
. Значит,
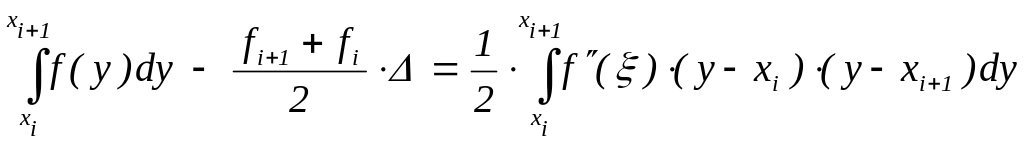 ,
,
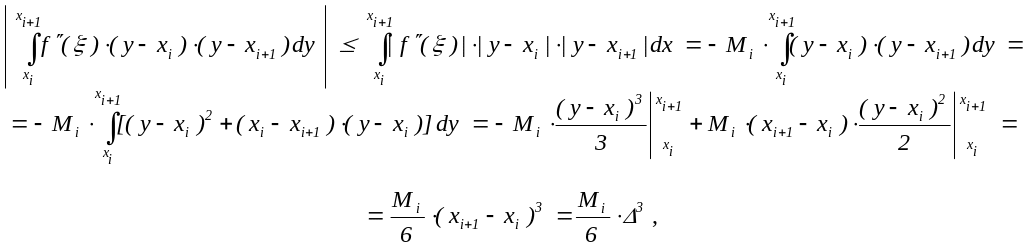
где Mi
=
![]() |f(x)|
.
|f(x)|
.
Таким образом,
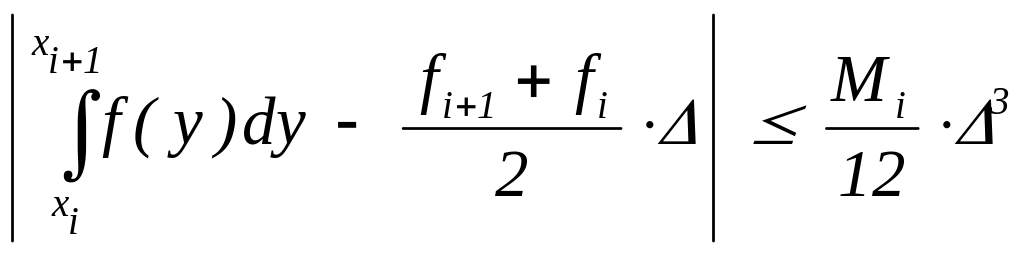 , и в общем виде
, и в общем виде
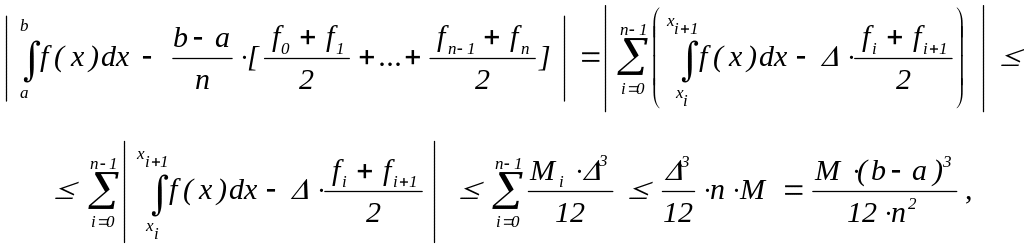
где M = |f(x)|.
Полученная оценка
позволяет по заданной погрешности
из неравенства
![]() находить число n
: n
>
находить число n
: n
>
![]() , вычислять
=
, и осознанно
применять формулу трапеций
, вычислять
=
, и осознанно
применять формулу трапеций
![]() .
.
Пример. Вычислить с точностью до 0,001 интеграл .
Оцениваем для
подынтегральной функции f(x)
=
![]() вторую
производную:
вторую
производную:
f(x)
=
![]() , f(x)
=
, f(x)
=
![]() ,
,
т.к. 3·x2 – 1 3·12 – 1 = 2, .
Вычисляем n
>
![]() ,
т.е. n
= 19. Теперь
пользуемся методом прямоугольников:
,
т.е. n
= 19. Теперь
пользуемся методом прямоугольников:
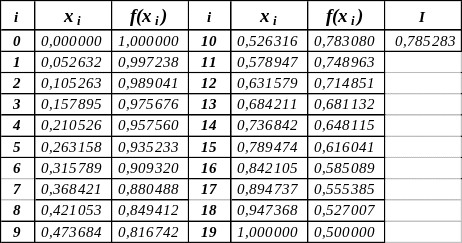
Сравнивая полученное значение интеграла с точным значением 0,785398, получим
| – I | |0,785398 – 0,785283| 0,000115 < 0,001,
что и требовалось.
