
- •Вместо введения: о погрешностях при решении прикладных задач
- •Глава I. Численные методы решения уравнений
- •§ 1. Задача локализации корней
- •Ограничение корней
- •Локализация корней
- •Простейший (грубейший) алгоритм локализации корней:
- •§ 2. Понятие об итерационных методах уточнения корней
- •Метод деления пополам (метод вилки)
- •§ 3. Методы хорд и касательных
- •Метод хорд для монотонных выпукло-вогнутых функций
- •Метод касательных для монотонных выпукло-вогнутых функций
- •§ 4. Метрические и банаховы пространства. Теорема о неподвижной точке
- •Матричные нормы
- •§ 5. Метод простой итерации
- •§ 6. Применение метода простой итерации к решению
- •Условие h([; ]) [; ] :
- •Глава II. Вычисления в линейной алгебре
- •§ 1. Метод Гаусса и его улучшения для повышения точности решения
- •§ 2. Метод простой итерации и метод Зейделя
- •§ 3. Подготовка к применению метода простой итерации
- •§ 4. Проблема собственных значений
- •Глава III. Численное интегрирование
- •§ 1. Метод прямоугольников
- •§ 2. Метод трапеций
- •§ 3. Метод Симпсона (параболическое интерполирование)
- •Глава IV. Некоторые методы аппроксимации функций
- •§ 1. Интерполяционный многочлен Лагранжа
- •§ 2. Интерполяционный многочлен Ньютона
- •§ 3. Метод наименьших квадратов
- •Глава V. Некоторые методы численного решения дифференциальных уравнений
- •Приложение: Сводка характеристик численных методов
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
§ 3. Методы хорд и касательных
Следующие методы похожи на метод деления пополам, но имеют квадратичную сходимость за счёт более осмысленного выбора точки xn+1 деления отрезка [n ; n].
М
 етод
хорд. Если
на отрезке [;
]
нужно найти
корень уравнения f(x)
= 0 для
непрерывной функции f
со свойством
f()·f()
< 0, то
можно действовать по аналогии с методом
деления пополам: строим последовательность
вложенных отрезков
етод
хорд. Если
на отрезке [;
]
нужно найти
корень уравнения f(x)
= 0 для
непрерывной функции f
со свойством
f()·f()
< 0, то
можно действовать по аналогии с методом
деления пополам: строим последовательность
вложенных отрезков
[0 ; 0] [1 ; 1] … [n ; n] [n+1 ; n+1 ] …,
на концах которых функция принимает значения противоположных знаков
полагаем x0 = = 0, 0 = , 0 = | – |, причём f(0)·f(0) < 0;
пусть уже известны xn , n , n , n , где f(n)·f(n) 0;
если f(n) = 0 или f(n) = 0, то корень найден, процесс завершён;
если n и |f(xn)| , то процесс завершён, xn – приближённое значение корня;
если n > или |f(xn)| > , то xn+1 = n –
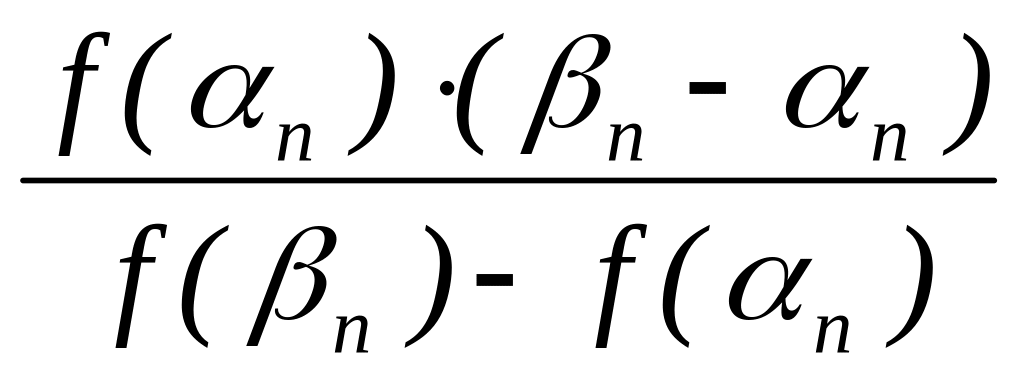 – точка пересечения с осью абсцисс
хорды
– точка пересечения с осью абсцисс
хорды
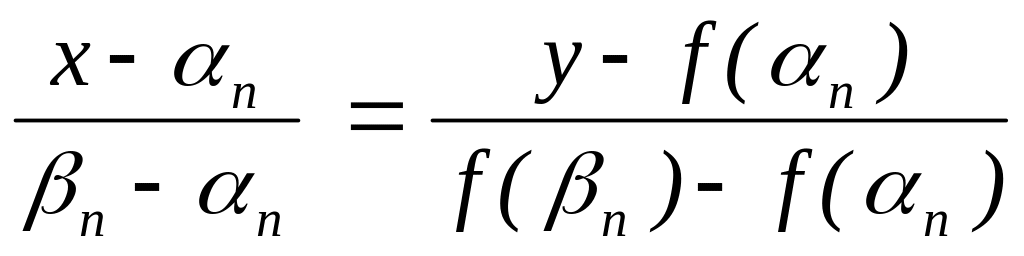 с концами в точках (n
; f(n))
и (n
; f(n)).
Полагаем
с концами в точках (n
; f(n))
и (n
; f(n)).
Полагаем
[n+1 ; n+1] = ,
n+1 = n+1 – n+1 , возврат к шагу 2.
Приведённый выше рисунок показывает, что этот метод может привести к результату для функций весьма общего вида. Однако всегда нужно иметь в виду, что при f(n) = f(n) вычисления по методу хорд становятся невозможными. Таким образом, для беспечного применения метода хорд функция f на отрезке [; ] должна быть инъективной.
Если функция f не слишком патологическая, то после локализации корня можно считать отрезок [; ] настолько малым, что функция f на нём монотонна и даже выпукла или вогнута. Тогда метод хорд можно упростить:

Метод хорд для монотонных выпукло-вогнутых функций
положим =
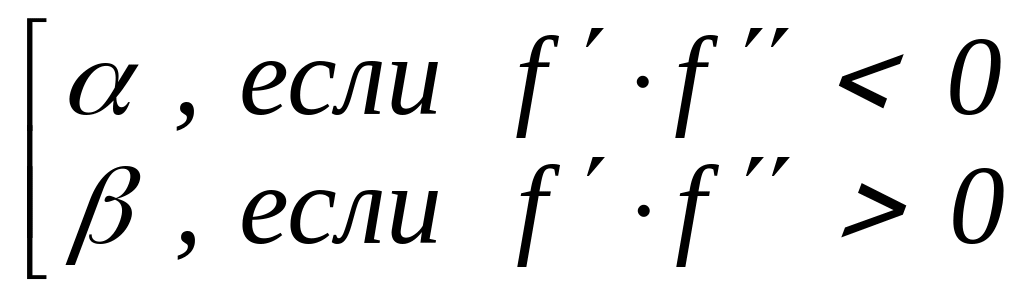 , x0
=
, x0
=
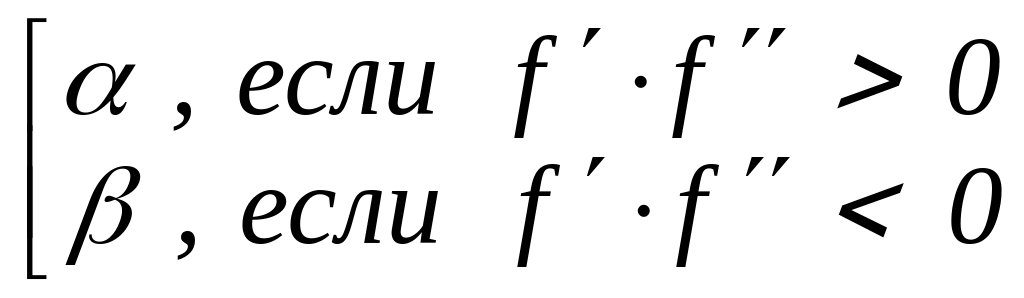 , 0
=
–
.
, 0
=
–
.пусть уже известны xn , n .
если f(xn) = 0, то корень найден, процесс завершён.
если n и |f(xn)| , то процесс завершён, xn – приближённое значение корня.
если n–1 > или |f(xn)| > , то
![]() – точка
пересечения с осью абсцисс хорды
– точка
пересечения с осью абсцисс хорды
![]() с концами в точках (
; f())
и (xn
; f(xn)),
n+1
= xn+1
– xn
, возврат к шагу 2.
с концами в точках (
; f())
и (xn
; f(xn)),
n+1
= xn+1
– xn
, возврат к шагу 2.
Здесь функция не предполагается дифференцируемой: символы f и f использованы лишь для удобного краткого обозначения знаков возрастания-убывания и выпуклости-вогнутости функции f (так, f > 0 обозначает возрастание, а f < 0 – убывание функции, f > 0 означает, что f выпукла вниз, а f < 0 – что f выпукла вверх). Таким образом, в случаях а), г) нужно положить = , x0 = , а в случаях б), в) – соответственно = , x0 = .
Теорема (о методе хорд). Пусть известен отрезок [; ], в котором заключён ровно один корень уравнения f(x) = 0, где функция f непрерывна, строго монотонна, всюду выпукла или вогнута на [; ] и f()·f() < 0. Тогда последовательность {xn}n N , определённая по методу хорд, сходится к корню r [; ]. При этих предположениях метод хорд имеет линейную скорость сходимости.
Доказательство. Для доказательства сходимости заметим, что последовательность {xn}n N монотонна.
Для определённости проведём рассуждения в случае в): функция f убывает и выпукла вниз. Последнее означает, что любая хорда лежит выше графика функции. Согласно алгоритму, = , x0 = , f() > 0, f(x0) < 0, т.е. x1 [; x0] и f(x1) < 0. Предположим, что доказаны неравенства x0 x1 … … xk > и f(xi) < 0 (0 i k). Тогда xk+1 – точка пересечения с осью абсцисс хорды с концами (; f()) и (xk ; f(xk)) – лежит между и xk , т.е. xk+1 xk . Кроме того, поскольку хорда лежит выше графика функции, а в точке xk+1 хорда пересекает ось абсцисс, то f(xk+1) < 0.
Итак, последовательность
{xn}n
N
монотонна
и ограничена (лежит на [;
]),
поэтому она имеет предел x.
Переходя к пределу
в неравенстве
f(xn)·f()
< 0, получим
f(x)·f()
0, так что
f(x)
f(),
x
. Поэтому
предельный переход в формуле xn+1
= xn
–
![]() приводит
к условиям x
= x
–
приводит
к условиям x
= x
–
![]()
![]() = 0, т.е. f(x)
= 0 и x
= r.
= 0, т.е. f(x)
= 0 и x
= r.
Оценим скорость сходимости:

Достаточно понять,
что величины
![]() ограничены:
если
с > 0 (
n
N
Mn
c),
то
n
N
|xn+1
– r|
c·|xn
– r|
, что и
требуется.
ограничены:
если
с > 0 (
n
N
Mn
c),
то
n
N
|xn+1
– r|
c·|xn
– r|
, что и
требуется.
Рассмотрим величину
![]() . Не трудно понять, что при выполнении
условий теоремы (в случаях а),
б),
в),
г)
на рисунках выше) верно
. Не трудно понять, что при выполнении
условий теоремы (в случаях а),
б),
в),
г)
на рисунках выше) верно
![]() и
и
![]() ,
так что вся величина положительна.
Поэтому достаточно доказать, неравенство
,
так что вся величина положительна.
Поэтому достаточно доказать, неравенство
![]() .
.
И меем,
f(xn)
= –(xn
– xn+1)tg
n
, f()
= (xn+1
– )tg
n
, откуда, вычитая, f(xn)
– f()
= –(xn
– )tg
n
. Поэтому
меем,
f(xn)
= –(xn
– xn+1)tg
n
, f()
= (xn+1
– )tg
n
, откуда, вычитая, f(xn)
– f()
= –(xn
– )tg
n
. Поэтому
![]() ,
,
что и требовалось.
Теорема доказана.
Следствие (о методе хорд для дифференцируемых функций). Пусть известен отрезок [; ], в котором заключён ровно один корень уравнения f(x) = 0, где функция f дважды непрерывно дифференцируема со знакопостоянными на этом отрезке производными f(x) и f(x), причём f()·f() < 0. Тогда последовательность {xn}n N , определённая по методу хорд, сходится к корню r [; ]. При этих предположениях метод хорд имеет линейную скорость сходимости.
Примеры: 1. Уточнить значение корня (точное его значение 0,25) для многочлена f(x) = 32·x3 – 48·x2 + 22·x – 3 на отрезке [0; 0,34] с точностью = 0,01.
Здесь f(x) = 22 – 96·x + 96·x2, f(x) = –96 + 192·x . Легко понять, что f < 0 и f > 0. Применяем метод хорд, беря = 0, x0 = 0,34.

Таким образом, приближённое значение корня 0,25 : 11 < 0,01 и f(x11) 0,01.
2.
Уточнить корень функции f(x)
=
![]() с точностью
до 0,001 на
отрезке [–1,3;
0,05].
с точностью
до 0,001 на
отрезке [–1,3;
0,05].
Здесь функция f(x) непрерывно дифференцируема дважды: f(0) = –1, f(0) = 0. Функция убывает, выпукла вниз, т.е. имеет случай в) : = –1,3, x0 = 0,05. Точное значение корня, очевидно, равно нулю.
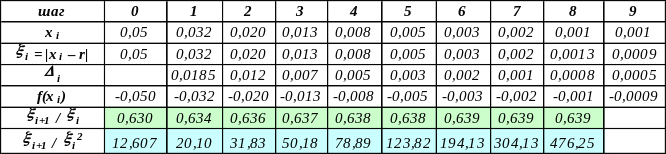
Видно, что универсальной константы c со свойством квадратичной сходимости |xn+1 – r| c·|xn – r|2 не существует. В то же время, конечно, имеет место линейная сходимость. Поэтому квадратичная сходимость метода хорд, о которой, как ни странно, говорится во многих учебниках (например, [7, стр. 95]) имеет место только для очень хороших ситуаций, в общем случае можно рассчитывать только на сходимость первого порядка.
Краткая характеристика метода хорд для монотонных выпукло-вогнутых функций приведена в приложении (таблица II) .
М
 етод
касательных.
Если на отрезке [;
]
требуется
найти корень уравнения f(x)
= 0 для
непрерывно дифференцируемой функции
f
со свойством
f()·f()
< 0, то
можно действовать как в методе хорд:
строим последовательность вложенных
отрезков
етод
касательных.
Если на отрезке [;
]
требуется
найти корень уравнения f(x)
= 0 для
непрерывно дифференцируемой функции
f
со свойством
f()·f()
< 0, то
можно действовать как в методе хорд:
строим последовательность вложенных
отрезков
[0 ; 0] [1 ; 1] … [n ; n] [n+1 ; n+1 ] … ,
на концах которых функция принимает значения противоположных знаков
полагаем в зависимости от ситуации либо x0 = = 0 , 0 = , либо x0 = = 0 , 0 = , 0 = | – |, причём f(0)·f(0) < 0;
пусть уже известны xn , n , n , n , где f(n)·f(n) 0;
если f(n) = 0 или f(n) = 0, то корень найден, процесс завершён;
если n и |f(xn)| , то процесс завершён, xn – приближённое значение корня;
если n > или |f(xn)| > , то xn+1 = xn –
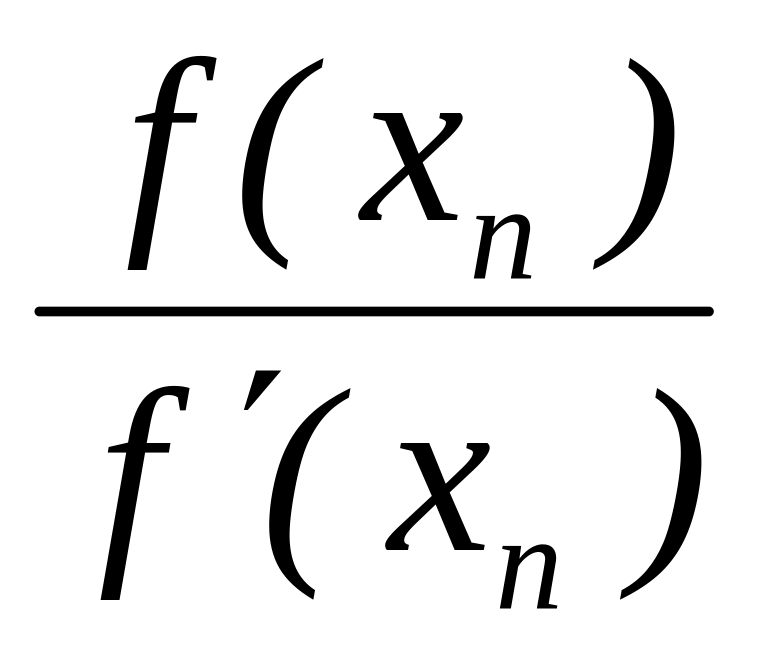 – точка пересечения с осью абсцисс
касательной y
= f(xn)
+ f(xn)·(x
– xn)
к графику функции в точке (xn
; f(xn)),
– точка пересечения с осью абсцисс
касательной y
= f(xn)
+ f(xn)·(x
– xn)
к графику функции в точке (xn
; f(xn)),
[n+1 ; n+1] = ,
n+1 = n+1 – n+1 , возврат к шагу 2.
П риведённый
выше рисунок показывает, что этот метод
может привести к результату для функций
весьма общего вида. Однако нужно иметь
в виду, что иногда вычисления по методу
касательных становятся некорректными:
например, точка xn+1
не всегда
принадлежит отрезку [;
]
или процесс “зацикливается” (см. рис.
слева). Таким образом, для беспечного
применения метода касательных функция
f
на отрезке [;
]
должна
удовлетворять дополнительным ограничениям.
риведённый
выше рисунок показывает, что этот метод
может привести к результату для функций
весьма общего вида. Однако нужно иметь
в виду, что иногда вычисления по методу
касательных становятся некорректными:
например, точка xn+1
не всегда
принадлежит отрезку [;
]
или процесс “зацикливается” (см. рис.
слева). Таким образом, для беспечного
применения метода касательных функция
f
на отрезке [;
]
должна
удовлетворять дополнительным ограничениям.
Е сли
функция f
не слишком
патологическая, то после локализации
корня можно считать отрезок [;
]
настолько малым, что функция f
монотонна на нём и даже выпукла или
вогнута. Тогда метод касательных можно
упростить:
сли
функция f
не слишком
патологическая, то после локализации
корня можно считать отрезок [;
]
настолько малым, что функция f
монотонна на нём и даже выпукла или
вогнута. Тогда метод касательных можно
упростить:
