- •Вместо введения: о погрешностях при решении прикладных задач
- •Глава I. Численные методы решения уравнений
- •§ 1. Задача локализации корней
- •Ограничение корней
- •Локализация корней
- •Простейший (грубейший) алгоритм локализации корней:
- •§ 2. Понятие об итерационных методах уточнения корней
- •Метод деления пополам (метод вилки)
- •§ 3. Методы хорд и касательных
- •Метод хорд для монотонных выпукло-вогнутых функций
- •Метод касательных для монотонных выпукло-вогнутых функций
- •§ 4. Метрические и банаховы пространства. Теорема о неподвижной точке
- •Матричные нормы
- •§ 5. Метод простой итерации
- •§ 6. Применение метода простой итерации к решению
- •Условие h([; ]) [; ] :
- •Глава II. Вычисления в линейной алгебре
- •§ 1. Метод Гаусса и его улучшения для повышения точности решения
- •§ 2. Метод простой итерации и метод Зейделя
- •§ 3. Подготовка к применению метода простой итерации
- •§ 4. Проблема собственных значений
- •Глава III. Численное интегрирование
- •§ 1. Метод прямоугольников
- •§ 2. Метод трапеций
- •§ 3. Метод Симпсона (параболическое интерполирование)
- •Глава IV. Некоторые методы аппроксимации функций
- •§ 1. Интерполяционный многочлен Лагранжа
- •§ 2. Интерполяционный многочлен Ньютона
- •§ 3. Метод наименьших квадратов
- •Глава V. Некоторые методы численного решения дифференциальных уравнений
- •Приложение: Сводка характеристик численных методов
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
§ 2. Интерполяционный многочлен Ньютона
Интерполяционный многочлен Лагранжа степени не выше n определён, как было доказано в прошлом параграфе, однозначно. Но записывать его можно по-разному.
Интерполяционный многочлен Ньютона получается, если многочлен Лагранжа степени не выше n – 1 записать в виде
Pn(x) = a0 + a1(x–x0) +…+ ak(x – x0)…(x – xk–1) +…+ an(x – x0)…(x – xn–1).
Неизвестные
коэффициенты ak
(0
k
n)
можно найти
последовательно, подставляя в эту
формулу x
= x0
, x1
, … , xn–1
. Для простоты проделаем вычисления
для равномерной
сетки xi+1
= xi
+ h
(0
i
n–1),
![]() .
.
y0 = Pn(x0) = a0 , a0 = y0 ,
y1
= Pn(x1)
= a0
+ a1(x1
– x0),
a1
=
![]() ,
,
y2 = Pn(x2) = a0 + a1(x2 – x0) + a2(x2 – x0)(x2 – x1),
![]() ,
,
. . .
Здесь удобно ввести
обозначения 1
yi
= yi+1
– yi
, 2
yi
=
yi+1
–
yi
= = (yi+2
– yi+1)
– (yi+1
– yi)
= yi+2
–2yi+1
+ yi
, … , k
yi
= k–1
yi+1
– k–1
yi
конечных разностей первого, второго,
… , k-го
порядков в точке yi
(при i
+ k
n).
Кроме того, будем считать, что 0
yi
= yi
(0
i
n).
В этих обозначениях для начальных
коэффициентов многочлена Ньютона
верны формулы
![]() , которые в
общем случае будут доказаны ниже.
, которые в
общем случае будут доказаны ниже.
Лемма (о конечных
разностях).
По аналогии
с формулой бинома Ньютона
![]() для конечных разностей выполняется
соотношение:
для конечных разностей выполняется
соотношение:
![]() (1
k
n).
Более общо:
(1
k
n).
Более общо:
![]() (1
k
n
– i)
и
(1
k
n
– i)
и
![]() (1
k
n).
(1
k
n).
Доказательство. Проведём индукцию по k N, доказывая сразу общую формулу .
При k
= 1 получаем
![]() – верно.
– верно.
Предположим, что формула верна для k = 1, … , m n – i и докажем её при k = m + 1. Если m = n – i, то доказывать уже нечего.
Если же m
< n
– i,
то m
+ 1
n
– i
и по
определению конечных разностей
m+1
yi
=
m
yi+1
–
m
yi
=
![]() =
=
![]()
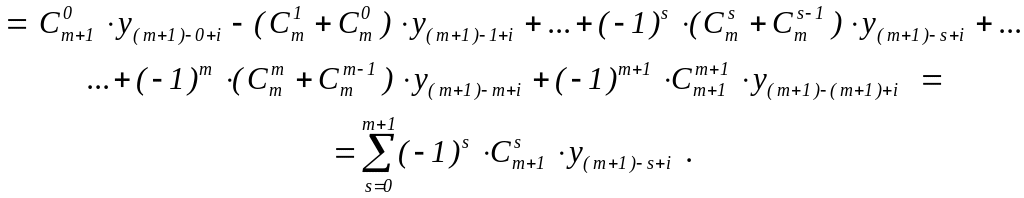
Последнее равенство
использует известное свойство биномиальных
коэффициентов
![]() .
.
Равенство (1 k n) можно вывести из доказанного:
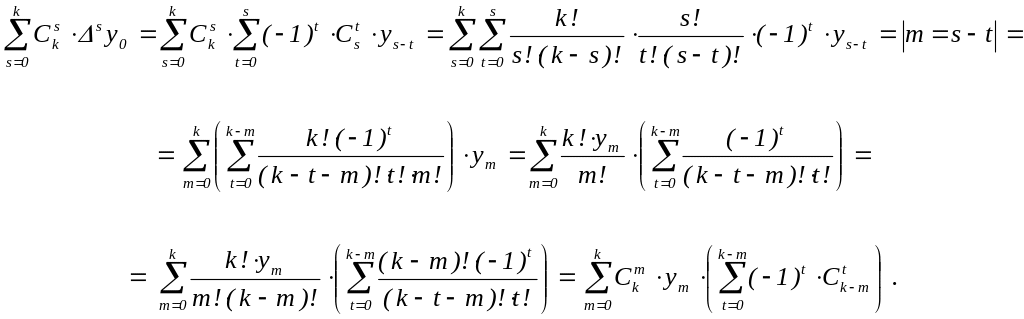
Выражение
![]() при k=
m
превращается
в 1,
а при k
– m
> 0 – в (1
– 1)k–m
= 0 (вспомните
бином Ньютона !). Поэтому от изучаемой
двойной суммы остаётся просто yk
, что и требовалось.
при k=
m
превращается
в 1,
а при k
– m
> 0 – в (1
– 1)k–m
= 0 (вспомните
бином Ньютона !). Поэтому от изучаемой
двойной суммы остаётся просто yk
, что и требовалось.
Лемма доказана.
Лемма (о коэффициентах многочлена Ньютона). Для коэффициентов ak многочлена Ньютона
Pn(x) = a0 + a1(x – x0) +…+ ak(x – x0)…(x – xk–1) +…+ an(x – x0)…(x – xn–1)
справедливы соотношения (0 k n).
Доказательство. Индукция по k .
База индукции, как показали ранее проведённые вычисления коэффициентов a0 , a1 , a2 , справедлива. Предположим, что формулы доказаны для k = 0, … , m и докажем их для k = m + 1.
После подстановки x = xm+1 в равенство
Pn(x)
=
![]() +am+1(x
– x0)…(x
– xm)+(x
– xm+1)p(x),
+am+1(x
– x0)…(x
– xm)+(x
– xm+1)p(x),
получим
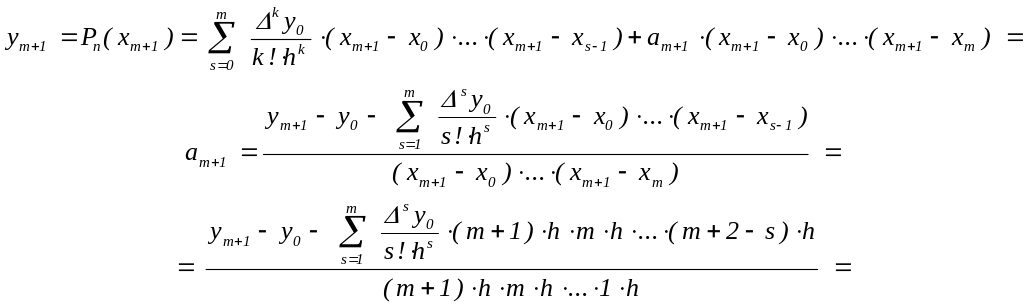
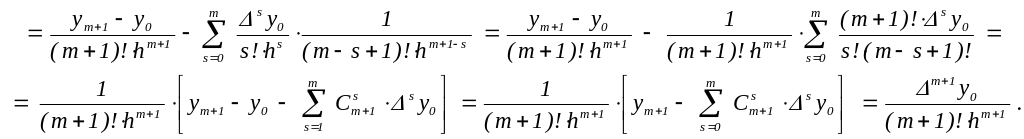
Лемма доказана.
Итак, по лемме
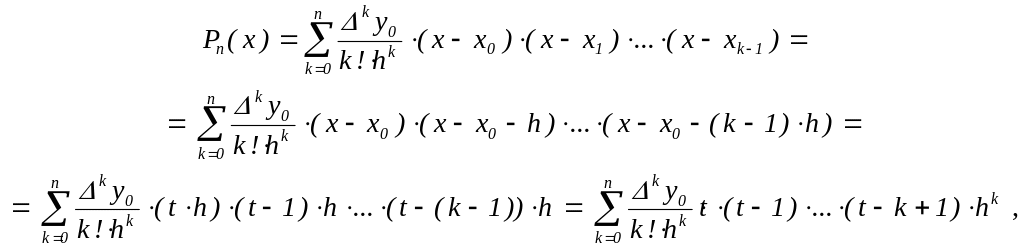
где
![]() .
.
Таким образом,
получаем
![]() – это (первый)
интерполяционный многочлен Ньютона,
который
можно записать в виде
– это (первый)
интерполяционный многочлен Ньютона,
который
можно записать в виде
![]() .
.
(Второй) интерполяционный многочлен Ньютона получается, если интерполяционный многочлен Лагранжа записать в виде
Pn(x) = a0 + a1(x–xn) +…+ ak(x – xn)…(x – xn–k+1) +…+ an(x – xn)…(x – x1),
беря за базовую точку не x0 а xn . Вычисления, аналогичные предыдущим приводят к следующим формулам:
![]() ,
,
![]() ,
,
где
![]() .
.
Пример. Найти многочлены Ньютона, принимающие в точках 1, 2, 3, 4 значения –4, –1, 0, 1.
Составим таблицу конечных разностей заданной в узлах функции, выделим в ней разности k y0 , k yn , где y0 = –4, yn = 1 и построим первый и второй интерполяционные многочлены Ньютона (заодно проверив их совпадение с многочленом Лагранжа).
x |
y |
y |
2 y |
3 y |
1 |
–4 |
|
|
|
3 |
||||
2 |
–1 |
–2 |
||
1 |
2 |
|||
3 |
0 |
0 |
||
1 |
|
|||
4 |
1 |
|
||
|
(зелёным цветом выделены разности k y0 , а синим – разности k yn).
Поэтому
![]()
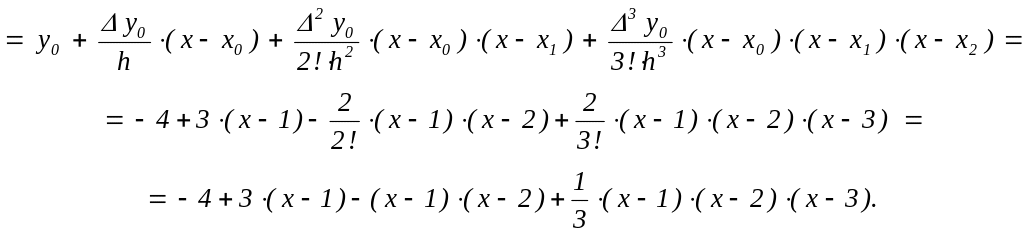
Найденный многочлен
можно записать, используя переменную
![]() :
:
P3(t
+ 1) = –4 + 3t
– t(t
– 1) +
![]() t(t
– 1)(t
– 2).
t(t
– 1)(t
– 2).
Точно так же, вторая интерполяционная формула Ньютона такова:
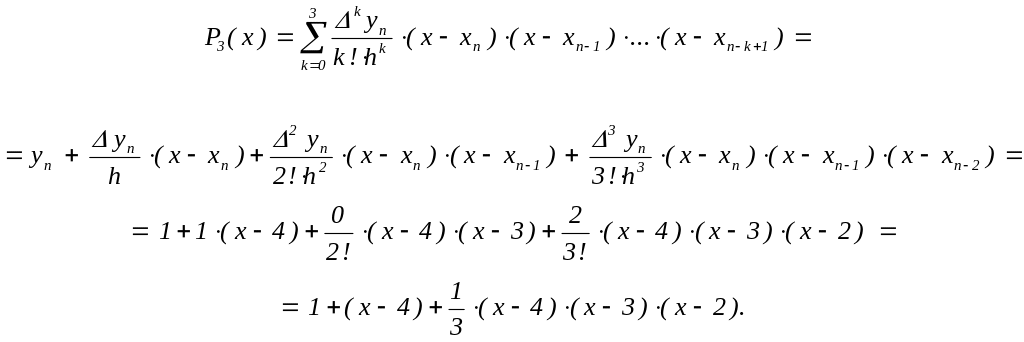 Этот
многочлен можно записать, используя
переменную
Этот
многочлен можно записать, используя
переменную
![]() :
:
P3(t + 4) = 1 + t + t(t+1)(t+2).
Раскрыв скобки, получим многочлен Лагранжа:
P3(x)
=
![]() (x–1)(x–2)(x–3)
– (x–1)(x–2)
+ 3(x–1)
– 4 =
(x–1)(x–2)(x–3)
– (x–1)(x–2)
+ 3(x–1)
– 4 =
= [(x–1)(x–2)(x–3) – 3(x–1)(x–2) + 9(x–1) –12] =
= [(x2 – 3x + 2)(x–3) – 3x2 + 18x – 27] = [x3 – 9x2 + 29x – 33] =
= [(x2 – 7x + 12)(x – 2) + 3x – 9] = 1 + (x–4) + (x – 4)(x – 3)(x – 2).
2. Используя формулу Ньютона, уплотнить таблицу значений заданной функции на отрезке [a; b] = [0,645 ; 0,695] с шагом h = 0,01.
![]()
Для вычисления с помощью многочлена Ньютона составим таблицу конечных разностей:
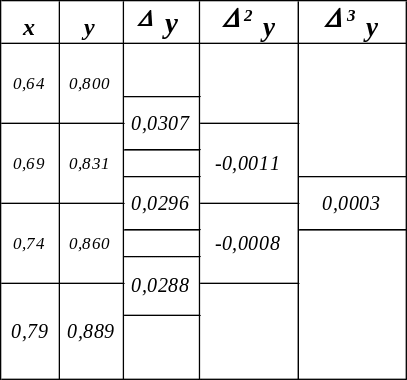
Поскольку вторые разности в пределах точности таблицы малы (их порядок примерно равен порядку точности заданных значений для y), в формуле Ньютона ограничимся тремя первыми слагаемыми:
![]() ,
,
где будем брать
x0
= 0,64, y0
= y(0,64)
= 0,800,
![]() , h
= 0,05. Вычисления
оформим в виде таблицы:
, h
= 0,05. Вычисления
оформим в виде таблицы:
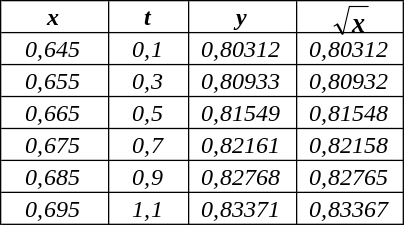
Из таблицы видно, что вблизи точки x = 0,64 результаты приближённых вычислений почти абсолютно совпадают с точными (вычисленными в среде Excel с помощью стандартной функции КОРЕНЬ(x)), но по мере удаления от этой точки точность приближений ухудшается. Можно улучшить ситуацию, используя ещё одну заданную в условии точку x = 0,69, производя вычисления по ближайшей из базовых точек 0,64 и 0,69:
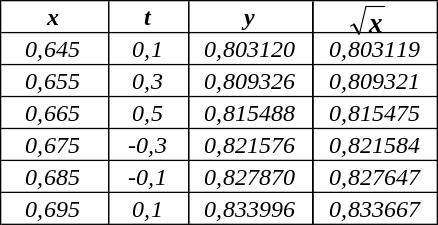
При x > 0,69 разумно брать значения y(0,69) = 0,831, y = 0,0288 и 2 y = –0,0008.
Приведённые в таблице значения y содержат избыточные знаки после запятой. Это сделано лишь для того, чтобы показать довольно высокую точность вычислений. Однако, окончательно нужно оставить только три цифры после запятой – так же, как и в исходных данных для величины y :