
- •Вместо введения: о погрешностях при решении прикладных задач
- •Глава I. Численные методы решения уравнений
- •§ 1. Задача локализации корней
- •Ограничение корней
- •Локализация корней
- •Простейший (грубейший) алгоритм локализации корней:
- •§ 2. Понятие об итерационных методах уточнения корней
- •Метод деления пополам (метод вилки)
- •§ 3. Методы хорд и касательных
- •Метод хорд для монотонных выпукло-вогнутых функций
- •Метод касательных для монотонных выпукло-вогнутых функций
- •§ 4. Метрические и банаховы пространства. Теорема о неподвижной точке
- •Матричные нормы
- •§ 5. Метод простой итерации
- •§ 6. Применение метода простой итерации к решению
- •Условие h([; ]) [; ] :
- •Глава II. Вычисления в линейной алгебре
- •§ 1. Метод Гаусса и его улучшения для повышения точности решения
- •§ 2. Метод простой итерации и метод Зейделя
- •§ 3. Подготовка к применению метода простой итерации
- •§ 4. Проблема собственных значений
- •Глава III. Численное интегрирование
- •§ 1. Метод прямоугольников
- •§ 2. Метод трапеций
- •§ 3. Метод Симпсона (параболическое интерполирование)
- •Глава IV. Некоторые методы аппроксимации функций
- •§ 1. Интерполяционный многочлен Лагранжа
- •§ 2. Интерполяционный многочлен Ньютона
- •§ 3. Метод наименьших квадратов
- •Глава V. Некоторые методы численного решения дифференциальных уравнений
- •Приложение: Сводка характеристик численных методов
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
Метод касательных для монотонных выпукло-вогнутых функций
полагаем x0 =
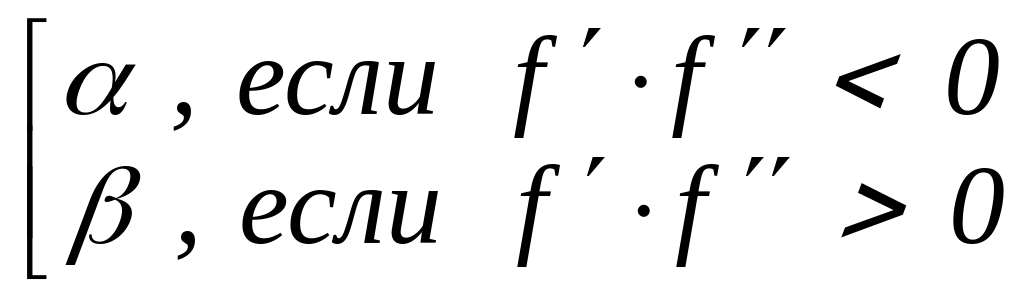 , 0
=
–
;
, 0
=
–
;пусть уже известны xn , n ;
если f(xn) = 0, то корень найден, процесс завершён;
если n и |f(xn)| , то процесс завершён, xn – приближённое значение корня;
если n–1 > или |f(xn)| > , то xn+1 = xn – – точка пересечения с осью абсцисс касательной y = f(xn) + f(xn)·(x – xn) к графику функции в точке (xn ; f(xn)), n+1 = xn+1 – xn , возврат к шагу 2.
Здесь функция не предполагается дважды дифференцируемой: символ f использован лишь для краткого обозначения знака выпуклости-вогнутости (f > 0 означает, что f выпукла вниз, а f < 0 – что f выпукла вверх). Таким образом, в случаях б), в) нужно положить x0 = , а в случаях а), г) – соответственно x0 = .
Теорема (о методе касательных). Пусть известен отрезок [; ], в котором заключён ровно один корень уравнения f(x) = 0, где функция f непрерывно дифференцируема, строго монотонна, всюду выпукла или вогнута на [; ] и f()·f() < 0. Тогда последовательность {xn}n N , определённая по методу касательных, сходится к корню r [; ]. Если f дважды непрерывно дифференцируема на [; ], то метод касательных имеет квадратичную скорость сходимости.
Доказательство. Для доказательства сходимости заметим, что последовательность {xn}n N монотонна.
Для определённости проведём рассуждения в случае в): функция f убывает и выпукла вниз. Последнее означает, что любая касательная лежит ниже графика функции. Согласно алгоритму, имеем x0 = , f(x0) > 0. Если положить = , то f() < 0, т.е. x1 [x0 ; ] и f(x1) > 0. Пусть уже доказано, что x0 x1 … xk < и f(xi) > 0 (0 i k). Тогда xk+1 – точка пересечения с осью абсцисс касательной к графику функции в точке (xk ; f(xk)) – лежит между xk и , т.е. xk+1 xk . Кроме того, поскольку касательная лежит ниже графика функции, а в точке xk+1 касательная пересекает ось абсцисс, то f(xk+1) > 0.
Итак, последовательность
{xn}n
N
монотонна
и ограничена (лежит на [;
]),
так что она имеет предел x.
Переходя к пределу в неравенстве
f(xn)·f()
< 0, получаем
f(x)·f()
0, поэтому
f(x)
f(),
x
. Кроме того,
f(x)
0. Действительно,
например, в случае в)
равенство
f(x)
= 0 вместе
с условиями убывания функции, выпуклости
вниз и f(x)
0 означало
бы, что f()
0, вопреки
f()·f()
< 0.
Теперь
предельный переход в формуле xn+1
= xn
–
даёт x
= x
–
![]()
= 0, т.е. f(x)
= 0 и x
= r.
= 0, т.е. f(x)
= 0 и x
= r.
Оценим скорость сходимости, рассматривая величину
|xn+1
– r|
=
![]() .
.
По формуле Тейлора,
f(xn)
= f(r)
+ f(r)·(xn
– r)
![]() ·(xn
– r)2
+ u(xn
– r),
где
·(xn
– r)2
+ u(xn
– r),
где
![]() ,
т.е. u(x)
= o(|x|2).
Аналогично, записывая по формуле
Тейлора f(xn)
= f(r)
+ f(r)·(xn
– r)
+ v(xn
– r),
где v(x)
= o(|x|),
получим:
,
т.е. u(x)
= o(|x|2).
Аналогично, записывая по формуле
Тейлора f(xn)
= f(r)
+ f(r)·(xn
– r)
+ v(xn
– r),
где v(x)
= o(|x|),
получим:
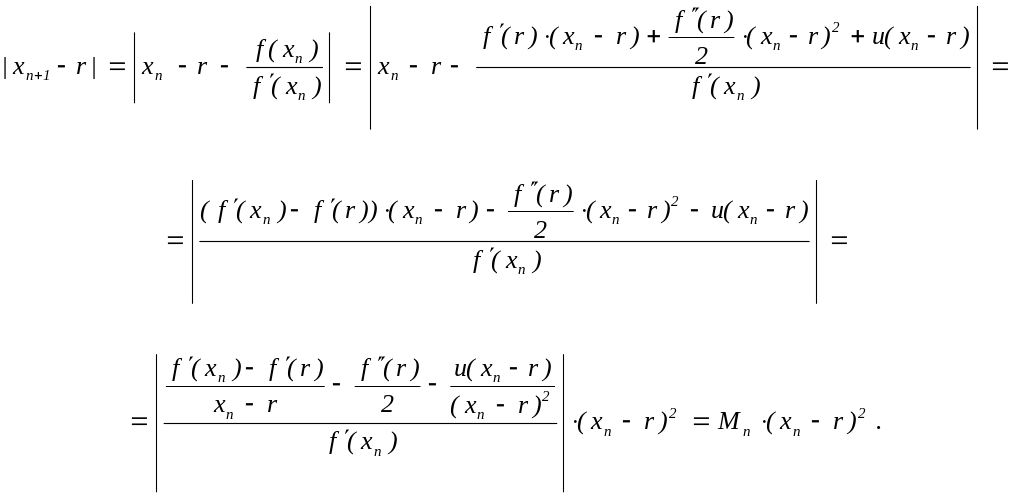
При этом величина
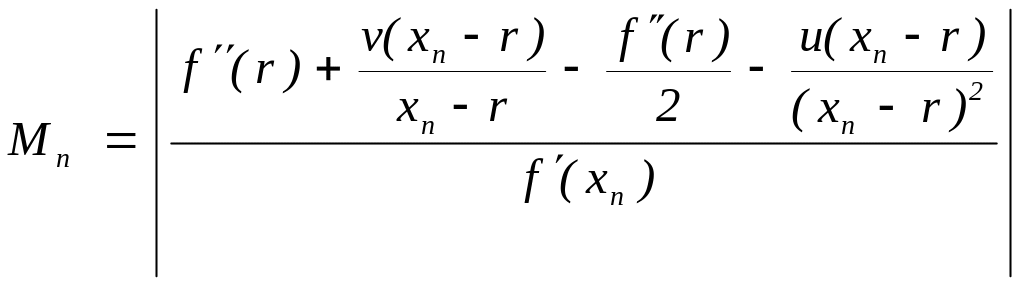 ограничена.
Это следует из существования предела
ограничена.
Это следует из существования предела
![]() .
.
Теорема доказана.
Замечание:
Для квадратичной сходимости метода
касательных существенно наличие второй
производной у функции. Действительно,
рассмотрим функцию f(x)
=
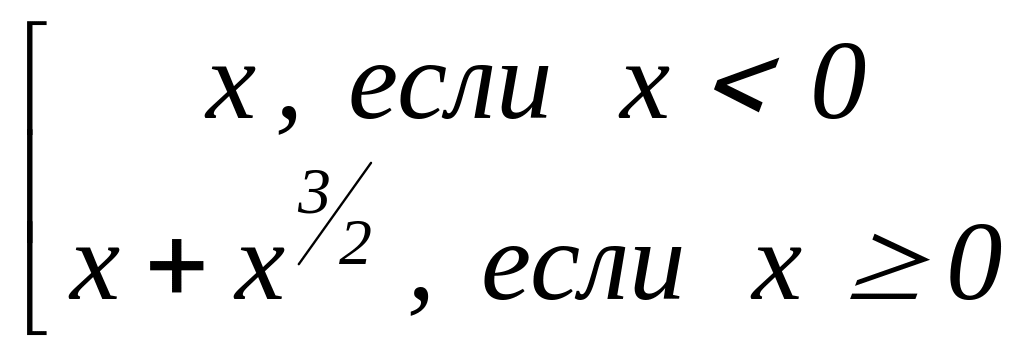 на интервале
[–1; 1].
Она непрерывно дифференцируема,
возрастающая, выпукла вниз, но не имеет
второй производной в своём корне –
точке r
= 0. Применение
метода касательных даёт следующие
результаты:
на интервале
[–1; 1].
Она непрерывно дифференцируема,
возрастающая, выпукла вниз, но не имеет
второй производной в своём корне –
точке r
= 0. Применение
метода касательных даёт следующие
результаты:
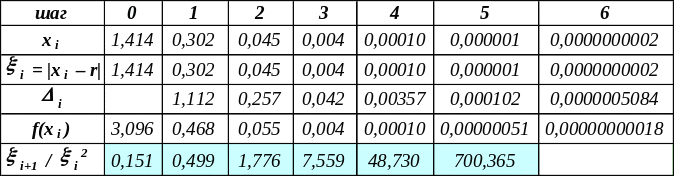
Поведение величины i+1 / i2 обусловлено тем, что
| xi+1
– 0 | = | xi
– 0 –
![]() | = | xi
–
| = | xi
–
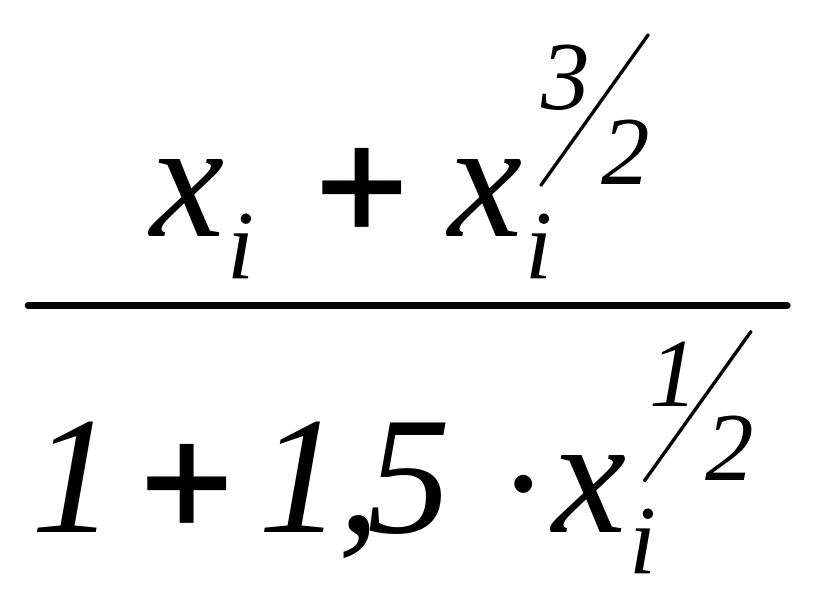 | = |
| = |
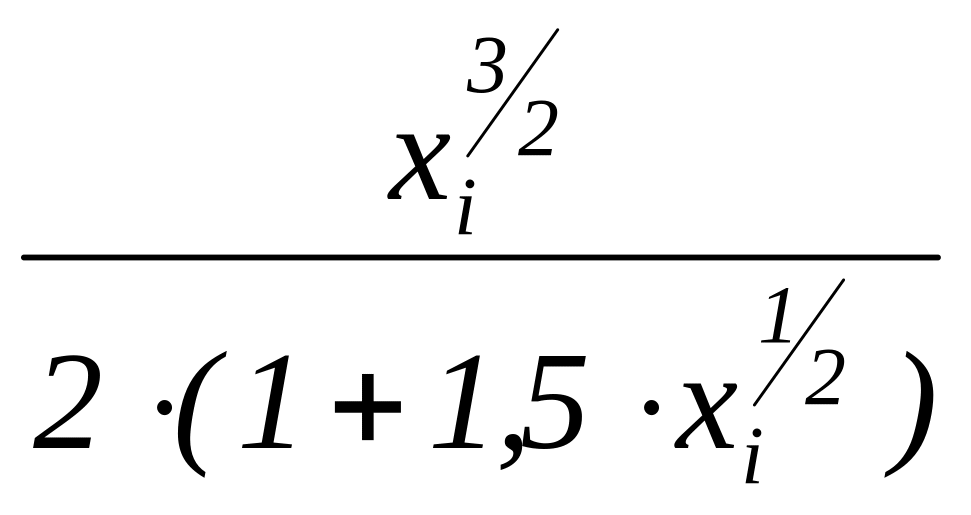 | .
| .
Поэтому
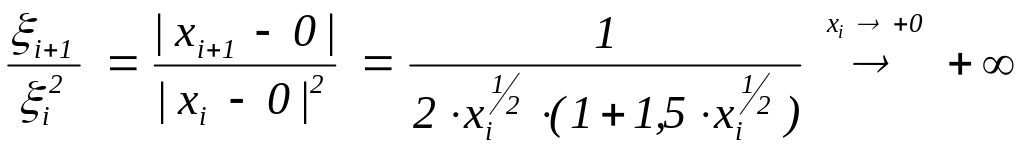 .
.
Примеры: 1. Для многочлена f(x) = 32·x3 – 48·x2 + 22·x – 3 уточнить значение корня на отрезке [0; 0,34] с точностью = 0,01. Точное значение корня, равно 0,25.
Здесь f(x) = 22 – 96·x + 96·x2, f(x) = –96 + 192·x . Легко понять, что f < 0 и f > 0 на [0; 0,34]. Применяем метод касательных, беря x0 = 0.
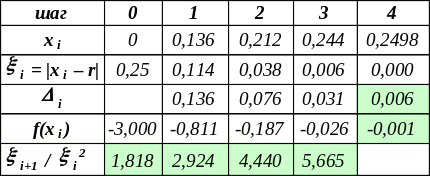
Приближённое значение корня 0,25, поскольку 4 < 0,006 < 0,01 и f(x4) –0,001 < 0,01.
2.
Уточнить корень функции f(x)
=
![]() на [–1,3;
0,05] с точностью
до 0,001.
на [–1,3;
0,05] с точностью
до 0,001.
Здесь функция f(x) непрерывно дифференцируема дважды: f(0) = –1, f(0) = 0 (?!). Функция убывает, выпукла вниз, т.е. имеет случай в), и x0 = –1,3. Точное значение корня, очевидно, равно нулю.
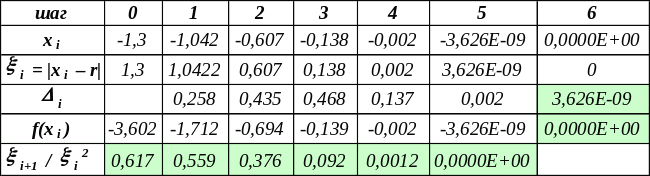
Видно, что имеет место квадратичная сходимость.
Краткая характеристика метода хорд для монотонных выпукло-вогнутых функций приведена в приложении (таблица III) .
