Министерство образования и науки Российской Федерации

Лукинова с. Г.

Математика

Высшая алгебра

Комплексные числа

Учебноe пособие

Красноярск 2010

Содержание
Введение
Комплексные числа
Многочлены
Теоретические вопросы
Теоретические упражнения
Расчетные задания
Литература

Введение

Настоящие методические указания соответствуют курса лекций по дисциплине «Высшая математика», они содержат теоретические вопросы, теоретические упражнения, расчетные задания (360 задач), справочный материал и примеры решения типовых задач.

Каждый студент учебной группы выполняет индивидуальное задание – один вариант содержит 12 задач, которые оцениваются 20 баллами.

Данное индивидуальное задание является одним из системы расчетных заданий, выполняемых при рейтинговой технологии обучения.

§1. Комплексные числа

Комплексными числами называются

упорядоченные пары действительных чисел, для которых определены операции:

• сложения ,

• умножения .

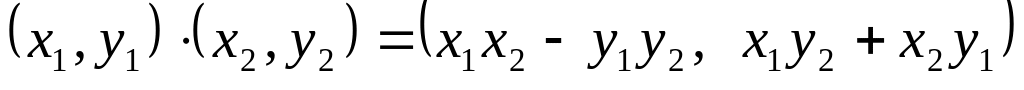Комплексное число записывается в виде

(алгебраическая форма),

- мнимая единица.

где - действительная часть;

- мнимая часть комплексного числа;

Всякое комплексное число может быть записано и в тригонометрической форме

или в показательной форме

,

где - модуль числа z;

- аргумент числа z;

; .

Два комплексных числа и равны тогда и только тогда, если и .

Число называются сопряженным комплексным числом.

Для возведения в степень комплексного числа используют формулу Муавра.

.

Корень ^ой степени из комплексного числа Z имеет различных значений, которые находятся по формуле

;

.

Приведем решения некоторых типовых задач.

Пример.

Найти значения выражений

а) ;

б) ;

Решение:

а) ;

б) Запишем число в тригонометрической форме

;

, тогда

.

По формуле Муавра получим или

.

в) Запишем число в тригонометрической форме , тогда , где

или

§2. Многочлены

Функция называется многочленом или полиномом степени .

Числа (действительные или комплексные) являются коэффициентами многочлена; переменная , вообще говоря, комплексная .

Число будет корнем многочлена , если

.

Теорема Безу

Для того, чтобы многочлен имел (комплексный) корень С, необходимо и достаточно, чтобы он делился на , то есть

,

где - некоторый многочлен степени .

Корень многочлена С называют простым корнем, если

и .

Число С называют корнем многочлена кратности К, если

и .

Основная теорема алгебры.

Всякий многочлен ^ой степени имеет, по крайней мере, один корень (действительный или комплексный).

Из этой теоремы следует, что многочлен имеет действительных и комплексных корней , среди них могут быть и кратные корни, таким образом, многочлен разлагается множители

, где .

Если коэффициенты многочлена являются действительными числами, то если есть корень , то комплексно сопряженное число также будет корнем .

В этом случае паре сопряженных комплексных корней и будет соответствовать в разложении многочлена множитель – квадратный трехчлен с отрицательным дискриминантом .

(Найдите, чему равны и , если , ).

Таким образом, многочлен , коэффициенты которого действительные числа, будет разложен на множители следующим образом:

, (1)

Здесь - действительные корни, кратности соответственно , а каждый квадратный трехчлен имеет отрицательный дискриминант.

Рациональной функцией или рациональной дробью называется отношение двух многочленов

.

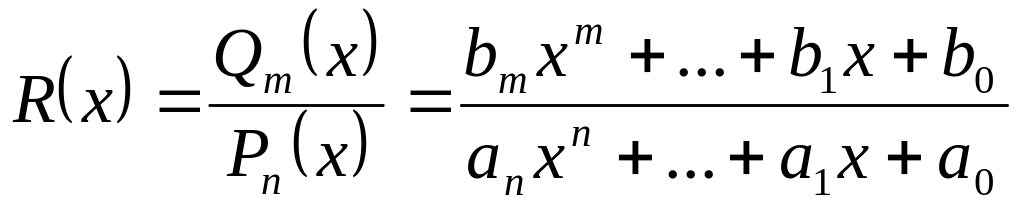Рациональная дробь будет правильной, если степень числителя меньше степени знаменателя , и неправильной, когда .

Рациональные функции вида

I ) ;

II ) ;

III ) ;

IV )

называют простейшими рациональными дробями. Здесь - действительные числа, а трехчлен имеет отрицательный дискриминант.

Пусть знаменатель правильной рациональной дроби разложен на множители по формуле (1). Тогда рациональную дробь можно представить и притом единственным образом в виде суммы простейших дробей, причем множителю соответствует дробь ; множителю соответствует сумма дробей ; множителю соответствует дробь ; множителю соответствует сумма дробей .

Поясним последнее утверждение на примерах.

Пример.

Следующие рациональные дроби разложить на сумму простейших дробей:

а) ;

Решение:

,

,

где - некоторые числа.

Чтобы их найти, приводим правую часть к общему знаменателю и приравниваем числители левой и правой частей:

.

Приравниваем коэффициенты при одинаковых степенях в обеих частях равенства:

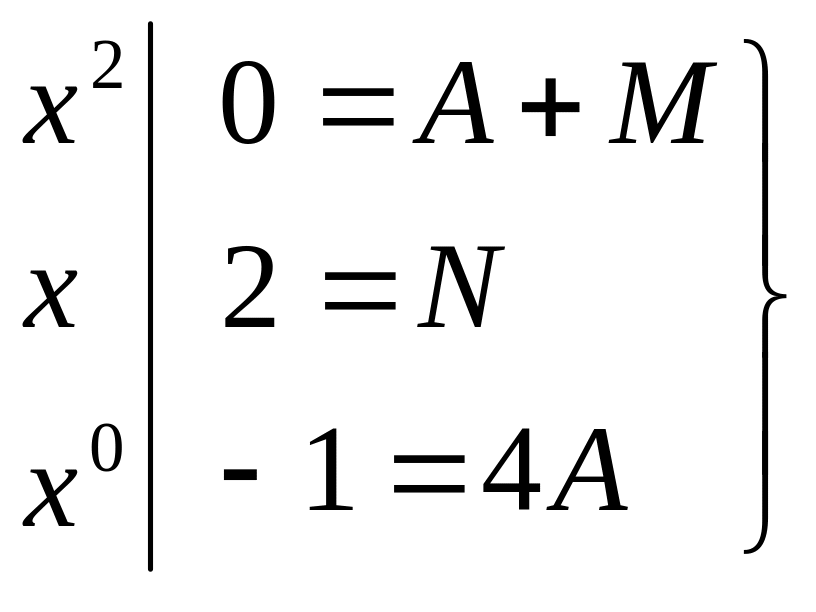
Решая систему, найдем

; ; , таким образом,

.

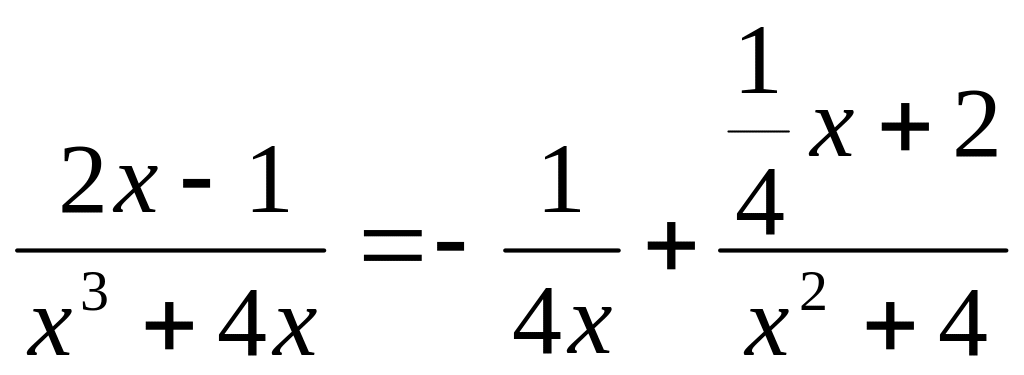б)

решая уравнение , нашли его корни , тогда , .

Дадим любые значения, например, равные корням знаменателя дроби , откуда ; , тогда .

в) заданная рациональная дробь – неправильная, поэтому разделим числитель на знаменатель (столбиком)

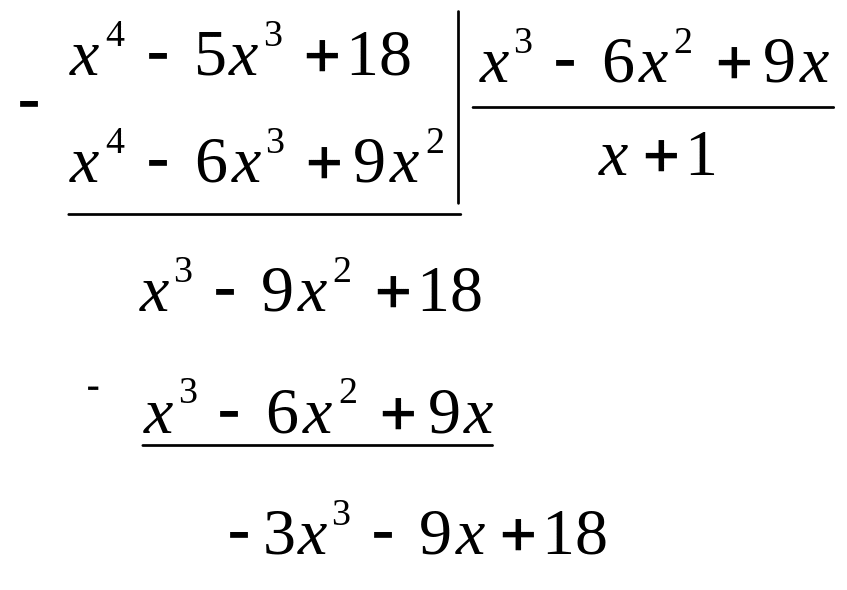
Таким образом

;

;

;

,

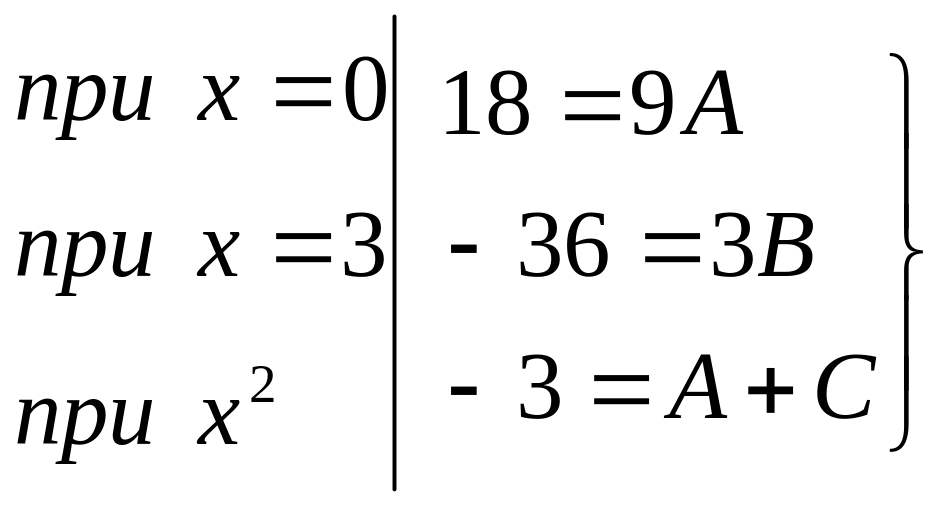, откуда ; ; тогда .