3. Операции над множествами

Определение 1.8. Множество C называется объединением (суммой) множеств А и В (пишется C=АВ или C=А+В), если xC тогда и только тогда, когда xА или xВ.

Иными словами, C=АВ={x: xА или xВ}.

Пример 1.2. Пусть А={1, 2, 3}, B={2, 3, 4, 5} и С=АВ.

Тогда C={1, 2, 3, 4, 5}.

Пример 1.3. Пусть А={1, 2, 3}, B={4, 5} и С=АВ.

Тогда C={1, 2, 3, 4, 5}.

Свойства операции объединения множеств

1. АВ=ВА (коммутативность).

2. А(ВС)=(АВ)С (ассоциативность).

3. АА=А.

Определение 1.9. Множество C называется пересечением (произведением) множеств А и В (пишется C=АВ или C=АВ), если xC тогда и только тогда, когда xА и xВ.

Иными словами, C=АВ={x: xА и xВ}.

Пример 1.4. Пусть А={1, 2, 3}, B={2, 3, 4, 5} и С=АВ. Тогда C={2,3}.

Пример 1.5. Пусть А={1, 2, 3}, B={4, 5} и С=АВ. Тогда C=.

Свойства операции пересечения множеств

1. АВ=ВА (коммутативность).

2. А(ВС)=(АВ) С (ассоциативность).

3. АА=А.

Справедливо также следующее свойство:

А(ВС)=(АВ) (А С) (дистрибутивность).

Определение 1.10. Множество C называется разностью множеств А и В (пишется C=А\В), если C={x: xА и xВ}.

Пример 1.6. Пусть А={1, 2, 3}, B={2, 3, 4, 5} и С=А\В. Тогда C={1}.

Пример 1.7. Пусть А={1, 2, 3}, B={4, 5} и С=А\В. Тогда C={1, 2, 3}.

Определение 1.11. Множество C называется симметрической разностью множеств А и В (пишется C=АΔВ), если C={x: x(А\В)(В\А)}.

Пример 1.8. Пусть А={1, 2, 3}, B={2, 3, 4, 5} и С=АΔВ.

Тогда C={1,4,5}.

Пример 1.9. Пусть А={1, 2, 3}, B={4, 5} и С=АΔВ.

Тогда C={1, 2, 3, 4, 5}.

Свойства симметрической разности множеств

1. АΔВ=ВΔА (коммутативность).

2. АΔ=ΔА (существование нейтрального элемента).

3. АΔА= (существование обратного элемента).

4. АΔ(ВΔС)=(АΔВ)ΔС).

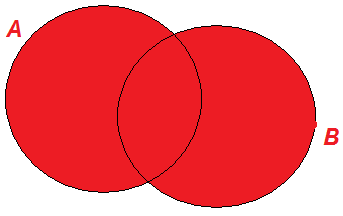
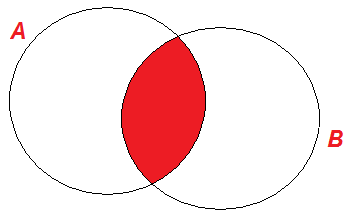
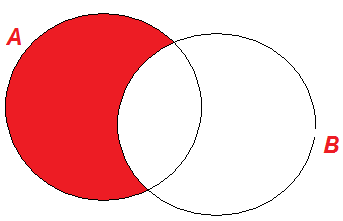
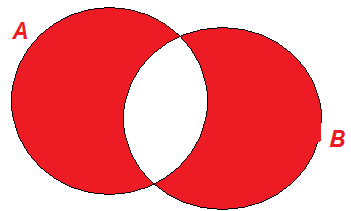
Операции над множествами допускают следующую наглядную иллюстрацию с помощью так называемых диаграмм Венна, названных в честь британского логика Дж.Венна. На этих диаграммах множества А и В – круги плоскости, а результат соответствующей операции – заштрихованная фигура (см. рис. 1).

Дж.Венн

АВ	АВ
А\В	АΔВ

Рис. 1. Операции над множествами: диаграммы Венна

Лекция №2. Алгебра высказываний

1. Высказывания и операции над ними.

2. Формулы алгебры высказываний.

3. Законы логики высказываний.

1. Высказывания и операции над ними

Математическая логика, предметом исследования которой является алгебра высказываний и исчисление предикатов, не слишком давно выделилась из логики – аналитической теории искусства рассуждения. Важнейший вопрос, на который отвечает математическая логика, звучит так: «Как определить справедливость суждения, полученного с помощью логических правил.

Основным понятием математической логики является высказывание.

Под высказыванием понимается утверждение, о котором можно судить истинно оно или ложно.

Например, следующие предложения являются высказываниями.

1. Париж – столица Франции.

2. Марс – спутник Земли.

3. М.Ю.Лермонтов – автор романа «Евгений Онегин».

4. Железо тяжелее воды.

5. Число 5 – корень уравнения x²–5x=0.

При этом первое, четвертое и пятое высказывания – это истинные высказывания, а второе и третье высказывания – ложные¹.

Не являются высказываниями следующие предложения.

1. Стой! Стрелять буду.

2. Пусть всегда будет Солнце!

3. Иванов похож на Петрова.

4. Ананасы вкуснее бананов.

На множестве высказываний W определяется так называемая функция истинности, принимающая значения в двухэлементном множестве {0,1} согласно следующей формуле:

Над высказываниями определяются следующие операции (логические связки), позволяющие на основе имеющихся высказываний строить новые.

1. Отрицание (обозначается ┐P, читается «не Р»).

Примеры. Если Р₁ это высказывание «Все люди смертны», то высказывание «Не все люди смертны» будет его отрицанием.

Отрицанием выказывания Р₂ «Педагогика – это наука», служит высказывание ┐Р₂ «Педагогика – это не наука».

2. Конъюнкция (обозначается читается «P и Q»).

Пример. Если Р – это высказывание «Множество натуральных чисел есть подмножество множества целых чисел», а Q – «Множество натуральных чисел есть подмножество множества рациональных чисел», то высказывание может звучать так «Множество натуральных чисел есть подмножество множества целых чисел и подмножество множества рациональных чисел».

3. Дизъюнкция (обозначается читается «P или Q»).

Пример. Если Р – это высказывание «Москва – столица России», а Q – «Москва – столица Франции», то высказывание может звучать так «Москва – столица России или столица Франции».

4. Импликация (обозначается P Q, читается «если P, то Q», или «из P следует Q», или «P достаточно для Q», или «Q необходимо для P»).

Пример. Если Р – это высказывание «12 делится на 6», а Q – «12 делится на 2», то высказывание P Q может быть сформулировано так «Если 12 делится на 6, то 12 делится на 2».

5. Эквивалентность (обозначается P  Q, читается «P равносильно Q», или «P тогда и только тогда, когда Q», или «P необходимо и достаточно для Q»).

Пример. Если Р – это высказывание «Железо тяжелее воды», а Q – «Вода легче железа», то высказывание P  Q может быть сформулировано так «Железо тяжелее воды, тогда и только тогда, когда вода легче железа».

Логические значения высказываний, получаемых в результате этих операций, определяются по логическим значениям исходных высказываний в соответствие с таблицей истинности (см. таб. 1).

Таблица 1

Таблица истинности

(P)	(Q)	(┐P)	( )	( )	(P Q)	(P  Q)
0	0	1	0	0	1	1
0	1	1	0	1	1	0
1	0	0	0	1	0	0
1	1	0	1	1	1	1

Примеры.

1. Высказывание P «АBА (пересечение множеств А и В есть подмножество множества А)» – истинное высказывание. В соответствие с таблицей истинности высказывание ┐P «Пересечение множеств А и В не является подмножеством множества А (АBА)» – ложное высказывание.

2. Пусть через P обозначено высказывание «Множество натуральных чисел есть подмножество множества рациональных чисел», через Q – «Множество рациональных чисел есть подмножество множества целых чисел». Тогда P истинное высказывание, а Q – ложное. И в соответствие с таблицей истинности ложными будут высказывания: ┐P, , P Q, P  Q. В то же время, истинными высказываниями будут:┐Q, , Q  P.

Высказывания, содержащие логические операции, называют сложными (в отличие от иных, которые называют простыми).

Множество высказываний с логическими операциями над ними называют алгеброй высказываний.