Предисловие

Данное учебно-методическое пособие предназначено в первую очередь, для студентов экономико-управленческих специальностей; может быть полезным для всех категорий студентов, изучающих в том или ином объёме высшую математику. Пособие является дополнением к конспектам лекций по высшей математике часть II, а также руководством для подготовки и проведения практических занятий.

Пособие разбито на учебные элементы — занятия, каждое занятие содержит справочный материал (основные определения, формулы, признаки и т.п.), необходимый для решения задач. Каждый учебный элемент содержит три блока задач (аудиторные, домашние и дополнительные), при составлении которых особое внимание уделено стандартным задачам, которых так не хватает для успешного хода учебного процесса. Приводятся методические рекомендации по решению определённого круга задач, в частности, алгоритмы их решения. Такая форма изложения позволяет сначала познакомиться с приёмами решения типовых задач и оформлением записи их решения, а затем приступить к выработке навыков в их самостоятельном решении. Тем не менее, в пособии довольно много сложных заданий. Приводится два варианта типовой контрольной работы, а также решение индивидуального домашнего задания.

Список обозначений:

▲ ▼ — важные определения;

 — «обратите особое внимание!»

► ◄ — начало и конец решения.

Занятие 1 Первообразная функция и неопределённый интеграл. Непосредственное интегрирование

Цели

Знать:

• Определения первообразной и неопределённого интеграла; их геометрический смысл;

• свойства неопределённого интеграла;

• таблицу интегралов от основных элементарных функций;

• основные методы интегрирования.

Уметь:

• Находить интегралы методом непосредственного интегрирования.

▼Функция F(x), определённая в промежутке (a;b), называется первообразной функции f(x) в этом промежутке, если для любого значения выполняется равенство

или dF(x)=f(x)dx (1) ▲

Пример. 1) Функция F(x)=х⁵ — первообразная функции f(x)=5х⁴ в промежутке , поскольку для всех х;

2) функция F(x)=lnx первообразная функции в промежутке , так как ;

3) функция F(x)=arcсosx — первообразная функции в интервале (-1;1), т.к. .

Теорема. Если F(x) — первообразная функции f(x) на промежутке (a;b),то множество всех первообразных для f(x) задаётся

Ф(х)=F(x)+С, (2)

где С — произвольная постоянная.

▼Совокупность всех первообразных для функции f(x) на промежутке (a;b) называется неопределённым интегралом от функции f(x) и обозначается ,

где — знак неопределённого интеграла,

функция f(x) — подынтегральная функция,

выражение f(x)dx — подынтегральное выражение.

Таким образом,

, (3)

где F(x) — некоторая первообразная для f(x), С — произвольная постоянная.

Свойства неопределённого интеграла

1. Производная неопределённого интеграла равна подынтегральной функции

; (4)

2. Дифференциал неопределённого интеграла равен подынтегральному выражению:

. (5)

3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

. (6)

Сравнивая свойства 2 и 3, можно сказать, что операции нахождения неопределённого интеграла и дифференциала взаимнообратны (для свойства 3 с точностью до постоянного слагаемого).

4. Постоянный множитель можно выносить за знак неопределённого интеграла:

, (k=const). (7)

5. Если функции f₁(x) и f₂(x)имеют первообразные, то функция f₁(x)+f₂(x) также имеет первообразную, причём

. (8)

6. (Инвариантность формулы интегрирования). Если , то и , где — произвольная функция, имеющая непрерывную производную.

Таблица простейших интегралов

; [1]

; [2]

; [3]

; [4]

; [5]

; [6]

; [7]

; [8]

; [9]

; [10]

[11]

; [12]

; [13]

; [14]

Все указанные формулы справедливы в тех промежутках, в которых определены соответствующие функции.

Метод интегрирования, при котором данный интеграл путём тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределённого интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Постановка задачи. Найти неопределённый интеграл непосредственным интегрированием.

План решения. 1. Проанализировать подынтегральную функцию. Непосредственное интегрирование основано на прямом использовании таблицы интегралов. Могут представиться следующие случаи:

• данный интеграл находится непосредственно по соответствующему табличному интегралу;

• данный интеграл после применения свойств 4 и 5 приводится к одному или нескольким табличным интегралам;

• данный интеграл после элементарных тождественных преобразований над подынтегральной функцией и применения свойств 4 и 5 приводится к одному или нескольким табличным интегралам.

2. Полученный результат, используя свойство 2 проверить дифференцированием.

№1. Найти интеграл, результат проверить дифференцированием:

1) ; 2) ; 3) .

►1) = = =

= = = .

Замечание. Несколько постоянных интегрирования можно объединить в одну, например вместо суммы С₁+С₂+С₃ можно написать С.

Проверка. =

= ;

2) Данный интеграл приведём к табличному следующим образом:

= = = =

= ;

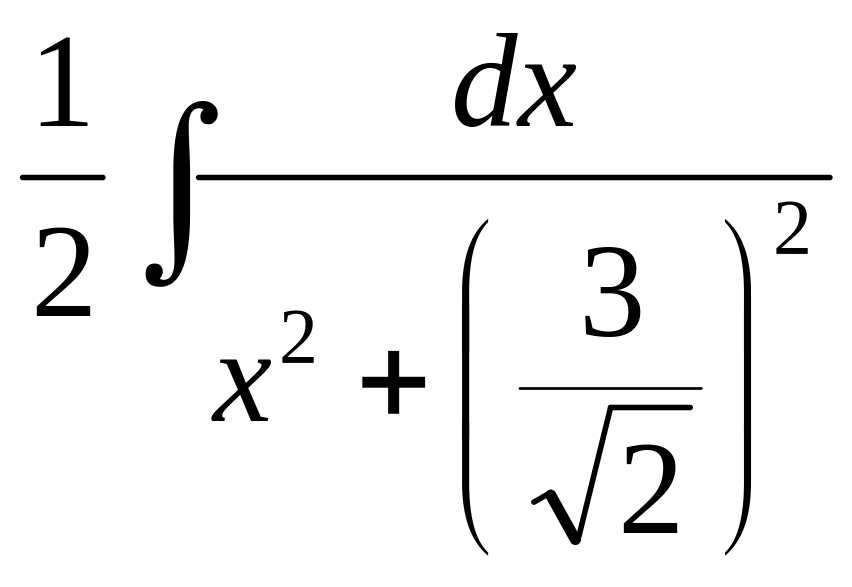Проверка. =

= ;

3) = = =

= ;

Проверка. = .

Аудиторное занятие

Пользуясь основными правилами и формулами интегрирования, найти следующие интегралы, результаты проверить дифференцированием:

Здесь и далее при записи ответов постоянную С мы фиксировать не будем.

№1. . Ответ: 3х.

№2. . Ответ: .

№3. . Ответ: .

№4. . Ответ: tgx-3 cosx.

№5. . Ответ: .

№6. . Ответ: .

№7. . Ответ: .

№8. . Ответ: .

№9. . Ответ: .

№10. .

Ответ: .

№11. . Ответ: .

№12. . Ответ: .

№13. . Ответ: .

№14. .

Указание. Применить формулу .

Ответ: -x-ctgx.

№15. . Ответ: .

№16. .

Указание. Применить формулу cos2x=cos²x-sin²x.

Ответ: -tgx-ctgx.

№17. .

Ответ: .

№18. .

Указание. Применить формулу .

Ответ: .

№19. . Ответ: .

№20. . Ответ: .

№21. . Ответ: .

№22. . Ответ: -2cos x.

№23. . Ответ: .

Домашнее задание

Пользуясь основными правилами и формулами интегрирования, найти следующие интегралы, результаты проверить дифференцированием:

№24. . Ответ: .

№25. . Ответ: .

№26. . Ответ: .

№27. . Ответ: .

№28. . Ответ: .

№29. . Ответ: .

№30. . Ответ: .

№31. 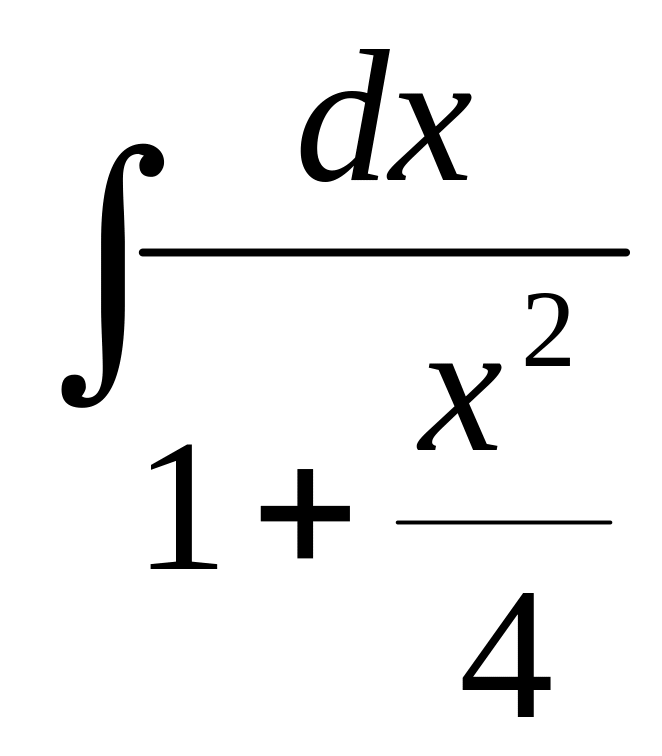. Ответ: .

№32. . Ответ: .

№33. . Ответ: x+cos x.

№34. . Ответ: .

№35. . Ответ: .

№36. . Ответ: .

№37. .

Указание. Учесть, что .

Ответ: tg x - ctg x.

№38. . Ответ: cos x-3ctg x.

№39. . Ответ: .

№40. .

Ответ: .

№41. . Ответ: .

№42. . Ответ: .

№43. . Ответ: .

№44. . Ответ: x-arctg x.

№45. . Ответ: .

Дополнительные задания

Пользуясь основными правилами и формулами интегрирования, найти следующие интегралы, результаты проверить дифференцированием:

№46. . Ответ: .

№47. . Ответ: .

№48. . Ответ: .

№49. . Ответ: -4cos x+2x⁴-11tg x.

№50. . Ответ: .

№51. . Ответ: .

№52.

Ответ: .

№53. . Ответ: .

№54. . Ответ: .

№55. . Ответ: .

№56. . Ответ: .

№57. . Ответ: .

№58. , где a,b — const.

Ответ: .

№59. , где a,b — const.

Ответ: .

№60. .

Указание. Учесть, что .

Ответ: .

№61. .

Указание. Учесть, что .

Ответ: .

№62. .

Указание. Учесть, что .

Ответ: .

№63. .

Указание. Воспользоваться формулой суммы кубов.

Ответ: sin x-cos x.