2. Оценка значимости различия средних значений двух выборок.

На основе данных из индивидуального задания составляется таблица, в которой представлены значения СВ соответственно первой и второй выборки.

2.1 Оценка значимости различия средних значений двух выборок с использованием критерия Стьюдента.

Оценивать существенность различия средних значений двух выработок с помощью критерия Стьюдента можно только в том случае, если выполняются два условия:

1. выборки должны подчиняться нормальному закону распределения;

2. дисперсии с разных выборок должны быть близкими.

Находим средние значения СВ для каждой из двух выборок по формуле:

(15)

Находим дисперсию выборок, указанных в варианте по формуле:

(16)

Если не известны обе дисперсии, и не предполагается, что они равны, то равенство двух средних проверяют с помощью приближённого экспериментального коэффициента Стьюдента:

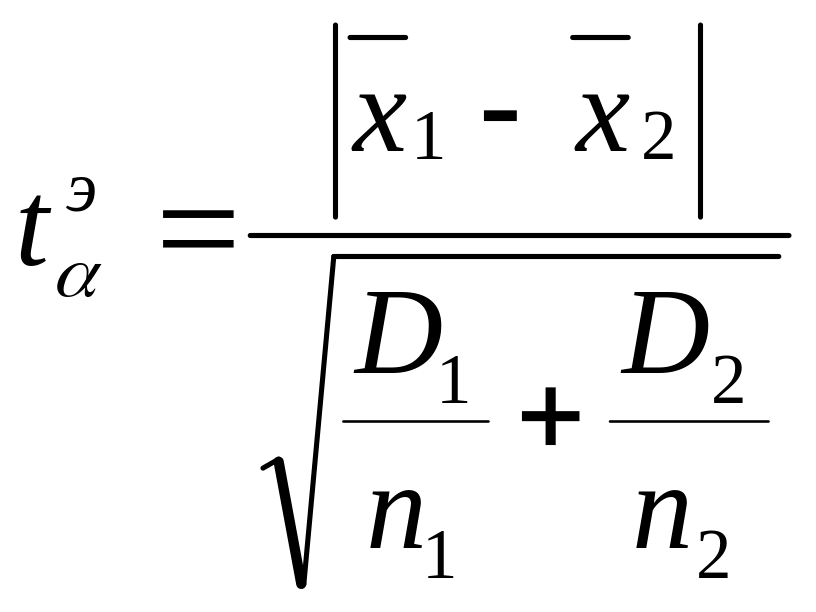, (17) где - рассчитанный коэффициент, D – дисперсия, n – количество наблюдений.

Для определения табличного значения коэффициента Стьюдента рассчитывается число степеней свободы при

(18)

Полученное экспериментальное значение сравнивают с табличным. Если различие коэффициентов существенно, то выборки не относятся к одной генеральной совокупности.

2.2 Оценка значимости различия средних значений двух выборок с использованием критерия Фишера.

Находим дисперсию выборок, указанных в варианте по формуле (2). Вычисляем расчетный критерий Фишера по формуле:

(19)

где - большая дисперсия..

Для определения табличного значения коэффициента Фишера рассчитывают число степеней свободы. Определяем табличное значение критерия Фишера при

Если , то расхождение дисперсий велико и различие средних значений существенно.

Вычисляется средневзвешенная дисперсия по формуле:

(20)

где - среднее значение дисперсий двух выборок.

.

Определяем табличное значение критерия Стьюдента при

Выполняем проверку с условием, что разность средних значений должна подчиняться :

(21)

(6)

Если неравенство выполняется то вычисляем коэффициент вариации

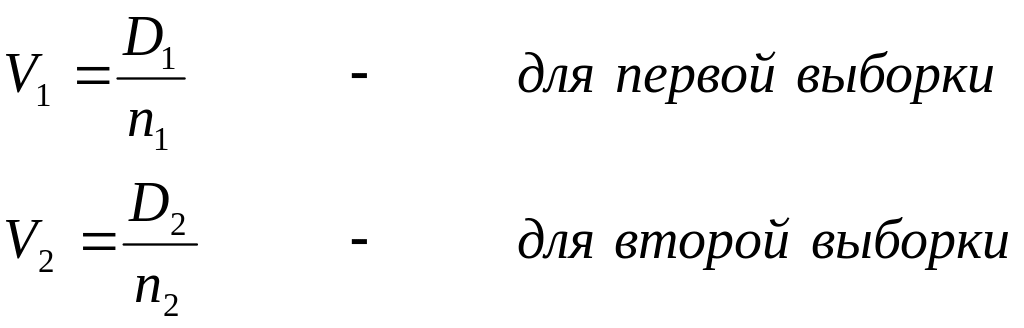(22)

Определяем величину Т и выполняем проверку с условием, что:

(23) (7)

Если неравенство выполняется, Средние значения данных выборок имеют значимые различия

3. Парный регрессионный анализ

3.1 Применение методов наименьших квадратов

Однофакторный анализ с уравнением регрессии вида .

Связь между факторами в статистике изучается методами корреля­ционно-регрессионного анализа. Когда изменение одной величины приво­дит к закономерному изменению других, то говорят, что они находятся в корреляционной зависимости. Если величины случайные, то стохастиче­ская связь между ними изучается методами корреляционного анализа. Результаты наблюдений обычно сводятся в корреляционные таблицы и выражаются графически. Для того чтобы рассчитать или прогнозировать значение искомой функции, необходимо определить ее уравнение связи с главными факторами.

Если все наблюдаемые величины лежат на прямой или кривой линиях регрессии, то говорят о точной корреляционной зависимости. Однако чаще всего наблюдаемые значения не совпадают с теоретической линией регрессии, то есть имеет место рассеяние, характеризующее тесноту связи изучаемой корреляционной зависимости. Коэффициент корреляции ха­рактеризует меру тесноты линейной связи.

Обращение коэффициента корреляции +1 или -1 является признаком линейной функциональной зависимости между х и у. Если или , то связь прямолинейна. Знак "+'' показывает, что с увеличением одной величины возрастает и другая. Знак "-" показыва­ет, что с возрастанием одной величины другая убывает. При прямолинейная корреляция отсутствует, но может иметь место криволинейная связь.

Если значения более 0,7—0,8, то можно считать связь сильной, при = 0,5—0,7 - связь средняя, а при =0,2—0,5 - связь слабая. Принято счи­тать, что линейной корреляции нет, если <0,4. Таким образом, для пря­молинейной связи коэффициент корреляции определяет меру связи между величинами. При малом значении коэффициента корреляции тес­нота прямолинейной связи между исследуемыми признаками оценива­ется критерием Стьюдента.

Различают два вида связи: 1) функциональная, 2) вероятностная (стохастическая).

Уравнение множественной регрессии должно быть адекватно изучаемому процессу. Коэффициенты в уравнении регрессии вычисляются методами матричной алгебры.

Задачу решают проведением прямой линии через набор опытных точек и в определении уравнения описывающего эту прямую. Обычно используется метод наименьших квадратов.

Тогда уравнения регрессии окажется уравнением вида

, (24)

где коэффициенты уравнения регрессии b₀ и b_1. Для их нахождения необходимо решить уравнения:

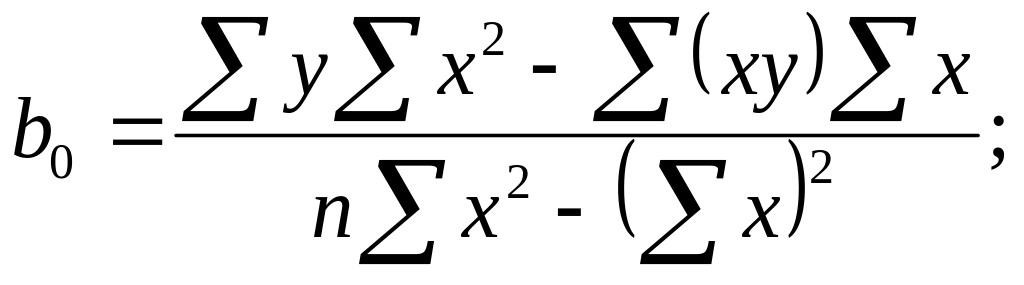(25)

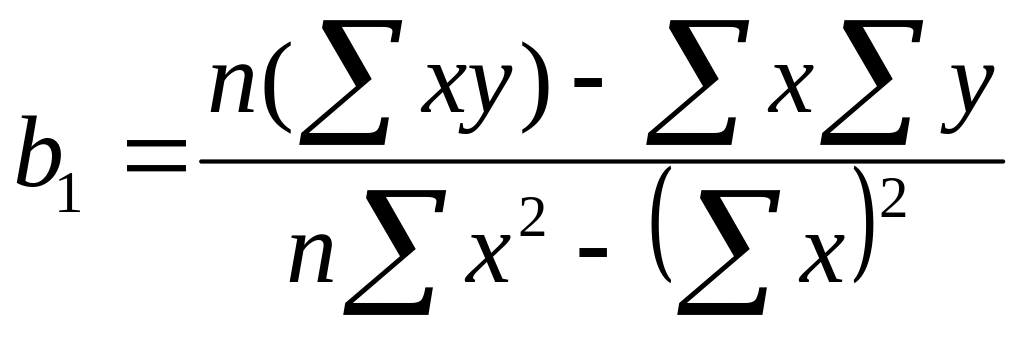. (26)

Коэффициент корреляции вычисляется по формуле:

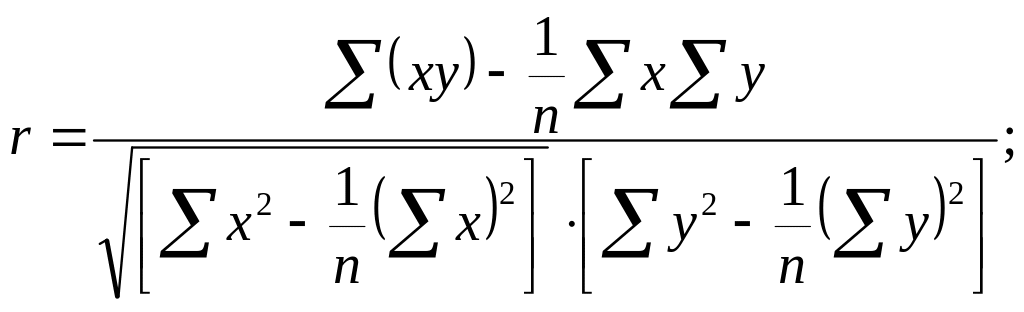(27)

Если опытные точки в декартовой системе координат явно лежат не вблизи прямой, то метод наименьших квадратов (МНК) неприменим.

Для применения МНК необходимо преобразовать систему координат таким образом, чтобы опытные точки располагались вблизи воображаемой прямой линии, т. е. выполнить так называемую линеаризацию (трансформировать систему координат).

Для расчетов используется программа Table Curve.

Исходные данные заносятся в таблицу №2. В процессе данной работы ведутся расчеты с помощью программы Table Curve и с ее помощью будет преобразована нелинейная парная регрессия в линейную.