
- •Кафедра математики и естественнонаучных дисциплин Борисова о.Н. Интегральное исчисление функций одной переменной
- •Введение
- •Неопределённый интеграл
- •Замена переменной
- •Интегрирование по частям
- •2) Интеграл вида , , .
- •3) Интеграл вида , .
- •Интегрирование рациональных функций
- •Интегрирование иррациональных функций
- •4) Избавление от иррациональности с помощью тригонометрических подстановок
- •2) Универсальная тригонометрическая подстановка.
- •Определенный интеграл
- •Замена переменной.
- •Интегрирование по частям.
- •Приложение определённого интеграла.
- •1) Площадь криволинейного сектора.
- •Контрольная работа №1
- •Решение варианта 0
- •Решение варианта 0
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант №13
- •Вариант №15
- •Вариант №23
- •Вариант №25
2) Интеграл вида , , .
![]()
![]()
![]()
![]()
![]()
![]()
3) Интеграл вида , .


![]()
![]()
![]()
Обозначим F(x)
произвольную первообразную функции
![]() ,
получим
,
получим
![]()
Выразим
![]() .
.
Интегрирование рациональных функций
Рациональной функцией, или рациональной
дробью, называется выражение вида
![]() ,
где
,
где
![]() и
и
![]() − многочлены степени n
и m соответственно.
Если n
− многочлены степени n
и m соответственно.
Если n
![]() m, дробь
называется неправильной, а если
n
m, дробь
называется неправильной, а если
n![]() m,
то правильной. Неправильную
рациональную дробь можно записать в
виде суммы многочлена и правильной
дроби. Для этого используется следующая
процедура деления с остатком многочлена
на многочлен (алгоритм Евклида).
m,
то правильной. Неправильную
рациональную дробь можно записать в
виде суммы многочлена и правильной
дроби. Для этого используется следующая
процедура деления с остатком многочлена
на многочлен (алгоритм Евклида).
Пусть
![]() ,
,
![]() при этом
при этом
![]() ,
n
m. Умножим
на
,
n
m. Умножим
на
![]() и вычтем получившееся выражение из
и вычтем получившееся выражение из
![]() .
В результате получим некоторый многочлен
.
В результате получим некоторый многочлен
![]() ,
степень которого строго меньше
,
степень которого строго меньше
![]() ,
и при этом
,
и при этом
![]() .
Если степень
.
Если степень
![]() все еще больше
все еще больше
![]() ,
применим описанный прием уже к многочлену
,
и так до тех пор, пока не получим «в
остатке» многочлен степени строго
меньше
.
Эта процедура деления разобрана далее
на нескольких примерах (деление
«уголком»).
,
применим описанный прием уже к многочлену
,
и так до тех пор, пока не получим «в
остатке» многочлен степени строго
меньше
.
Эта процедура деления разобрана далее
на нескольких примерах (деление
«уголком»).
Правильная рациональная дробь называется простой, если она принадлежит к одному из нижеперечисленных типов

Примеры простых дробей:
![]()
Любая правильная рациональная дробь может быть представлена как сумма простых дробей с подходящими коэффициентами. Такое разложение находят методом неопределенных коэффициентов, который мы проиллюстрируем на одном конкретном примере. Рассмотрим функцию:
![]() .
(1)
.
(1)
Составим комбинацию простых дробей, в знаменателях которых присутствуют все возможные делители знаменателя исходной функции:
![]()
После приведения этих пяти дробей к общему знаменателю получим:
![]() (2)
(2)
Приравняв числители (1) и (2), получим уравнение
![]() (3)
(3)
Соотношение (3) должно быть выполнено при всех значениях х. Подставим в (3) пять (по числу неизвестных коэффициентов A, B, C, D, E) различных значений х и получим систему уравнений на A, B, C, D, E:

Можно показать, что у такой системы
всегда существует единственное решение.
Решив эту систему (например, методом
Гаусса), получим требуемое представление
![]()
![]()
Интегрирование любой простой дроби всегда сводится к интегрированию табличных функций. Приведем несколько наиболее типичных примеров:
1)
![]()
2)

3)
 .
.
![]() Кратный неразложимый квадратный
многочлен в знаменателе дроби.
Кратный неразложимый квадратный
многочлен в знаменателе дроби.

1 способ. Интегрирование по частям.
![]()

2 способ. Замена переменной.

=
Интегрирование иррациональных функций
Большинство иррациональных функций не интегрируется в элементарных функциях. Есть лишь некоторые классы иррациональных функций, интегрирование которых с помощью той или иной замены переменной может быть сведено к интегрированию рациональных функций.
1) Интегралы вида
![]() где
где
![]() − рациональная функция, а
− рациональная функция, а
![]() −
натуральные числа. Метод интегрирования
– замена x=
−
натуральные числа. Метод интегрирования
– замена x=![]() ,
где N – наименьшее
общее кратное чисел
.
,
где N – наименьшее
общее кратное чисел
.
Пример:

![]()
2) Интегралы
![]() Метод интегрирования – замена
Метод интегрирования – замена
![]() =
=
![]() .
.
Пример:

=
3) Интегралы вида
![]() где m, n
и p – рациональные
числа (дифференциальный бином). Интегралы
такого вида сводятся к элементарным
функциям только при следующих соотношениях
параметров m, n
и p.
где m, n
и p – рациональные
числа (дифференциальный бином). Интегралы
такого вида сводятся к элементарным
функциям только при следующих соотношениях
параметров m, n
и p.
Обозначим N наименьшее общее кратное знаменателей дробей m и n. Тогда имеется три случая интегрируемости для дифференциального бинома.
А) p – целое число.
Метод интегрирования – замена
![]()
Б)
![]() – целое число. Метод интегрирования –
замена
– целое число. Метод интегрирования –
замена
![]() ,
где s – знаменатель
дроби p.
,
где s – знаменатель
дроби p.
В)
+ p – целое число. Метод
интегрирования – замена
![]() ,
где s – знаменатель
дроби p.
,
где s – знаменатель
дроби p.
Проиллюстрируем случаи Б) и В) на примерах.
i)
![]() .
.
Для данного интеграла
![]() ,
,
![]() ,
,
![]() .
Поскольку
.
Поскольку
![]() ,
избавиться от иррациональности можно,
взяв за новую переменную интегрирования
радикал
,
избавиться от иррациональности можно,
взяв за новую переменную интегрирования
радикал
![]() .
.



ii)
![]()
Для данного интеграла
![]() ,
,
.
Поскольку
,
,
.
Поскольку
![]() ,
избавиться от иррациональности можно,
взяв за новую переменную интегрирования
радикал
,
избавиться от иррациональности можно,
взяв за новую переменную интегрирования
радикал
![]() .
.
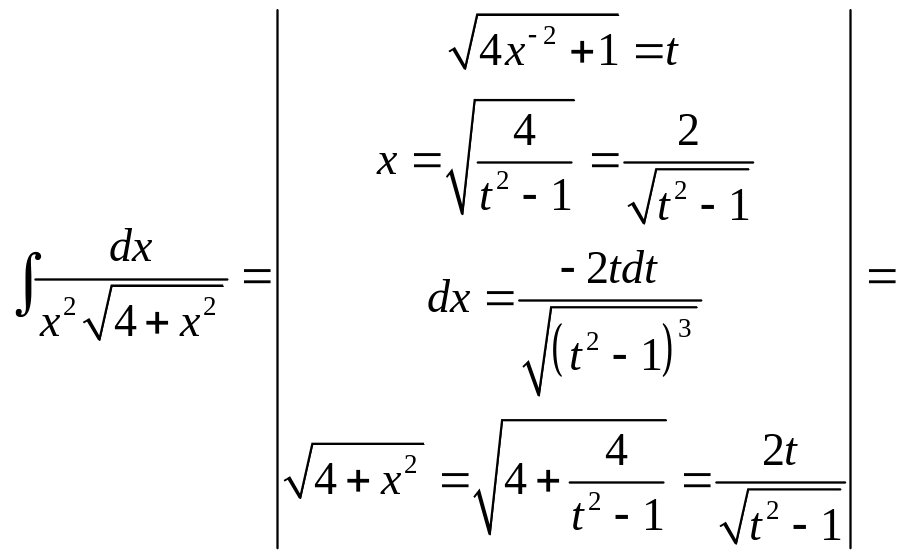
 .
.
