§ 5.5. Примеры электростатических полей.

1. Поле точечного заряда и системы точечных зарядов.

Напряженность поля точечного заряда выражают формулы (5.4.1) и (5.4.2). Из формулы (5.2.8) следует, что потенциал поля точечного заряда

(5.5.1)

Поле системы точечных зарядов позволяет рассчитать принцип суперпозиции (формула 5.4.4), соответственно, φ=Σφ_i. На рис.19 показаны силовые линии поля положительного и отрицательного точечных зарядов и поля диполя. Диполь – два точечных разноименных зарядов одинаковой величины. В одной из точек поля диполя показано построение вектора напряженности с помощью принципа суперпозиции. Силовые линии – воображаемые, но их можно сделать видимыми (вспомните лекционные демонстрации).

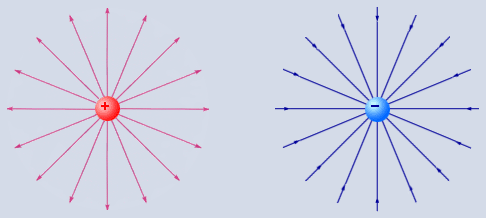
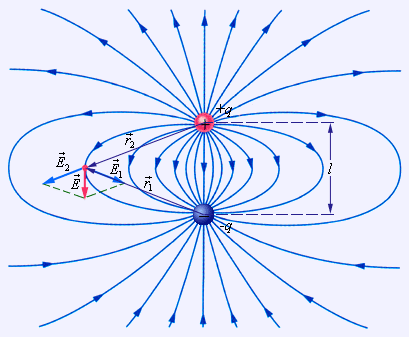
Рис 19

Н а рис. 20 представлены три электростатических поля: точечного заряда, диполя и двух одинаковых положительных заряда. Эквипотенциальные линии синие, силовые линии – красные.

2. Поле однородно заряженной бесконечной нити.

Н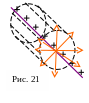 а рис. 21 показан отрезок нити (фиолетовая линия), на нити равномерно распределен заряд (его обозначили знаками «плюс»). На каждом элементе длины dl содержится заряд dq, линейная плотность заряда  = dq/dl=const. Понятно, что поле обладает цилиндрической симметрией. Это значит, что линии напряженности (оранжевые векторы) направлены по радиусам прямого цилиндра, ось которого совпадает с нитью. В качестве замкнутой поверхности рассмотрим часть прямого цилиндра радиусом r и длиной l с осью на нити. На рисунке он показан пунктирными линиями. Силовые линии пересекают боковую поверхность цилиндра по нормали, создавая поток ES_бок=E2rl, и скользят вдоль оснований цилиндра, не создавая потока сквозь них. Суммарный заряд, заключенный внутри этой поверхности q= l. Подставляя эти результаты в формулу (5.3.1), получаем:

(5.5.2)

3. Бесконечная однородно заряженная плоскость.

Поверхностная плотность заряда  =dq/dS=const. Из соображений симметрии ясно, что силовые линии равномерно выходят из плоскости перпендикулярно к ней в обе стороны, если плоскость заряжена положительно, и входят в нее, если заряд плоскости отрицательный. (Сделайте рисунок самостоятельно). С каждой стороны плоскости линии напряженности направлены в противоположные стороны, но густота их одинакова. В качестве замкнутой поверхности выберем поверхность прямого цилиндра, образующие которого перпендикулярны заряженной плоскости, а основания параллельны ей. Силовые линии скользят по его боковой поверхности и пересекают оба основания параллельно нормали к каждому основанию. Суммарный поток равен 2ES. Суммарный заряд, находящийся внутри поверхности, q=ES. Из теоремы Гаусса получаем:

E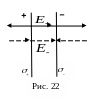 = /2₀ (5.3.3)

4) Плоский конденсатор.

Он образован двумя бесконечными разноименно заряженными плоскостями с одинаковой плотностью зарядов: ₊= _-= = const (рис. 22). На рисунке обозначены заряды плоскостей и нарисовано по одной силовой линии полей этих зарядов. Согласно принципу суперпозиции , так что

E= /₀ , внутри конденсатора (5.3.4)

Е=0, снаружи конденсатора (5.3.5)

Плоский конденсатор является источником однородного электрического поля, во всех точках которого векторы напряженности одинаковы, а силовые линии – параллельные прямые, проведенные с равномерной плотностью, при этом поле сосредоточено в пространстве между пластинами. Разумеется, реальный плоский конденсатор имеет пластины конечных размеров, и вблизи его краев поле неоднородное. Но чем меньше расстоянием между пластинами по сравнению с линейным размером пластин, тем точнее электростатическое поле в центральной части объема конденсатора соответствует однородному. Для получения однородного поля на практике используют плоский конденсатор.

5. Поле равномерно заряженной сферы.

Из соображений симметрии ясно, что силовые линии – радиальные прямые⁵. Такое поле называется сферически симметричным. Легко посчитать поток через любую сферическую поверхность радиуса r, центр которой совпадает с центром заряженной сферы: ES=E4r². Если радиус поверхности интегрирования равен или больше радиуса сферы R (r  R), то находящийся внутри поверхности интегрирования заряд равен заряду сферы q. Если r<R, то внутри поверхности интегрирования нет заряда. Применяя теорему Гаусса, получаем: равномерно заряженная сфера снаружи создает такое же поле, как точечный заряд, помещенный в ее центр (см. формулы 5.4.1 и 5.4.2.); внутри сферы поля нет, Е=0.