1.1.2. Принципи побудови матричних, пірамідальних і прямокутних дешифраторів

Матричним називають дешифратор, кожна вихідна функція якого реалізовується окремою схемою. Тим самим матричний дешифратор являє собою сукупність схем, не пов'язаних між собою по елементах. Оскільки вихідні функції дешифратора являють собою кон’юнкції вхідні змінних, схема, що реалізовує їх в матричному дешифраторі, є однокаскадною або багатокаскадною суперпозицією зі схем збігу. Якщо число входів в схемі збігу менше або дорівнює числу входів схеми дешифратора, то схема буде однокаскадною. В іншому випадку кількість каскадів буде більшою одиниці і залежить від співвідношення числа входів, схеми дешифратора і схем збігу.

Інші назви матричних дешифраторів – лінійні дешифратори, експонентні декодувальні мережі і т.д.

Приклад 1. Розглянемо побудову схеми матричного дешифратора, реалізуючої конституанти для трьох змінних , за допомогою тривходових схем І. В якості розрізнювачів взяті тригери Tг₁, Tг₂, Tг₃. Їх виходи реалізовують прямі і інверсні сигнали змінних, тобто x₁ x₁, x₁ і , .

Відповідно до викладеного принципу побудови матричних дешифраторів і заданого числа коиституант необхідно побудувати вісім тривхідних схем І.

Оскільки в першу конституанту всі три змінні входять в інверсному вигляді, то всі входи схеми І₁ з'єднують з інверсними виходами тригерів. Аналогічним чином два входи схеми І₂ сполучені з інверсними виходами триггеров Tг₁ і Tг₂, а третій - з прямим виходом тригера Tг₃ і т. д. Схема, побудована таким чином, показана на рис. 1.2.

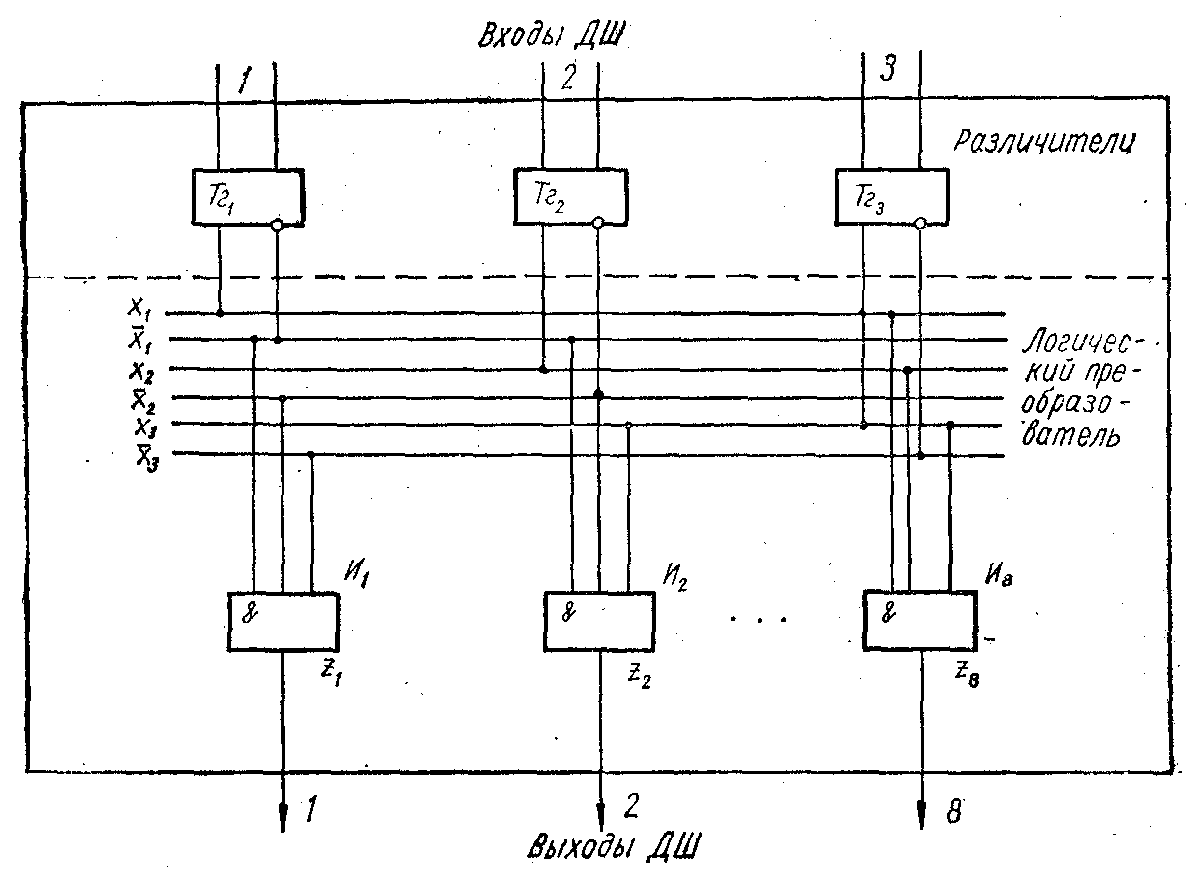
Рис. 1.2. Схема побудови матричного дешифратора

Пірамідальним дешифратором називають багатокаскадну схему, будь-яка вихідна функція якого в кожному каскаді утвориться як кон’юнкція вхідної змінної і деякої функції попереднього каскаду, що не залежить від цієї змінної. Вихідними функціями першого каскаду пірамідального дешифратора є також кон’юнкції.

Пірамідальні дешифратори в порівнянні з матричними характеризуються більш економною реалізацією за рахунок використання при їх побудові деяких загальних елементів для різних вихідних функцій.

На практиці при побудові пірамідального дешифратора будують матричний дешифратор для будь-яких двох змінних, наприклад х₁ і х₂. Максимальне число таких схем дорівнює чотирьом. Їх виходи з'єднують з входами схем збігів другого каскаду, куди подаються також сигнали третьої змінної, наприклад х₃. Максимальне число схем цього каскаду може бути рівним 8.

Схеми збігів будують так: до одного входу кожної з перших чотирьох схем підключають один з виходів першого каскаду, а до другого входу – вихід х₃ третьої змінної; входами кожної з других чотирьох схем збігів є також один з виходів першого каскаду і інверсний вихід третьої змінної.

Виходи цих схем збігів також є загальними для схем наступного каскаду. Аналогічним чином будують схеми збігів подальших каскадів, для кожного з яких справедливі вирази:

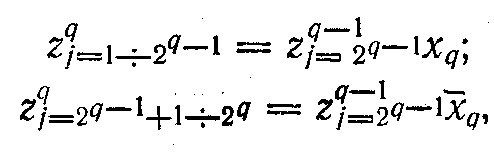
де j – номер функції; q – номер каскаду; х_q і – змінна і її інверсія; – конституанта q-гo каскаду. При повному дешифраторі для п змінних останнім буде п – 1-й каскад.

Приклад 2. Розглянемо побудову пірамідального дешифратора для трьох змінних при початкових даних прикладу 1.

Схема складається з двох каскадів, в першому з яких реалізовуються кон'юнкції змінних х₁ і х₂, а у другому – задані початкові вирази. Як видно з рис. 1.3, а, двовходові схеми збігів першого каскаду будують аналогічно схемам матричного дешифратора. Входами другого каскаду є виходи чотирьох схем збігів першого каскаду і тригера Тг₃. Перший вхід схеми І₁ другого каскаду сполучений з виходом І₁ першого каскаду, а другий вхід – з інверсним виходом Тг₃; перший вхід схеми І₁ сполучений з виходом Тг₃ першого каскаду, а другий вхід – з тим же інверсним виходом Тг₃ і т. д. Входи останньої схеми збігу сполучені з виходами схеми збігу І₁ першого каскаду і прямого виходу Тг₃.

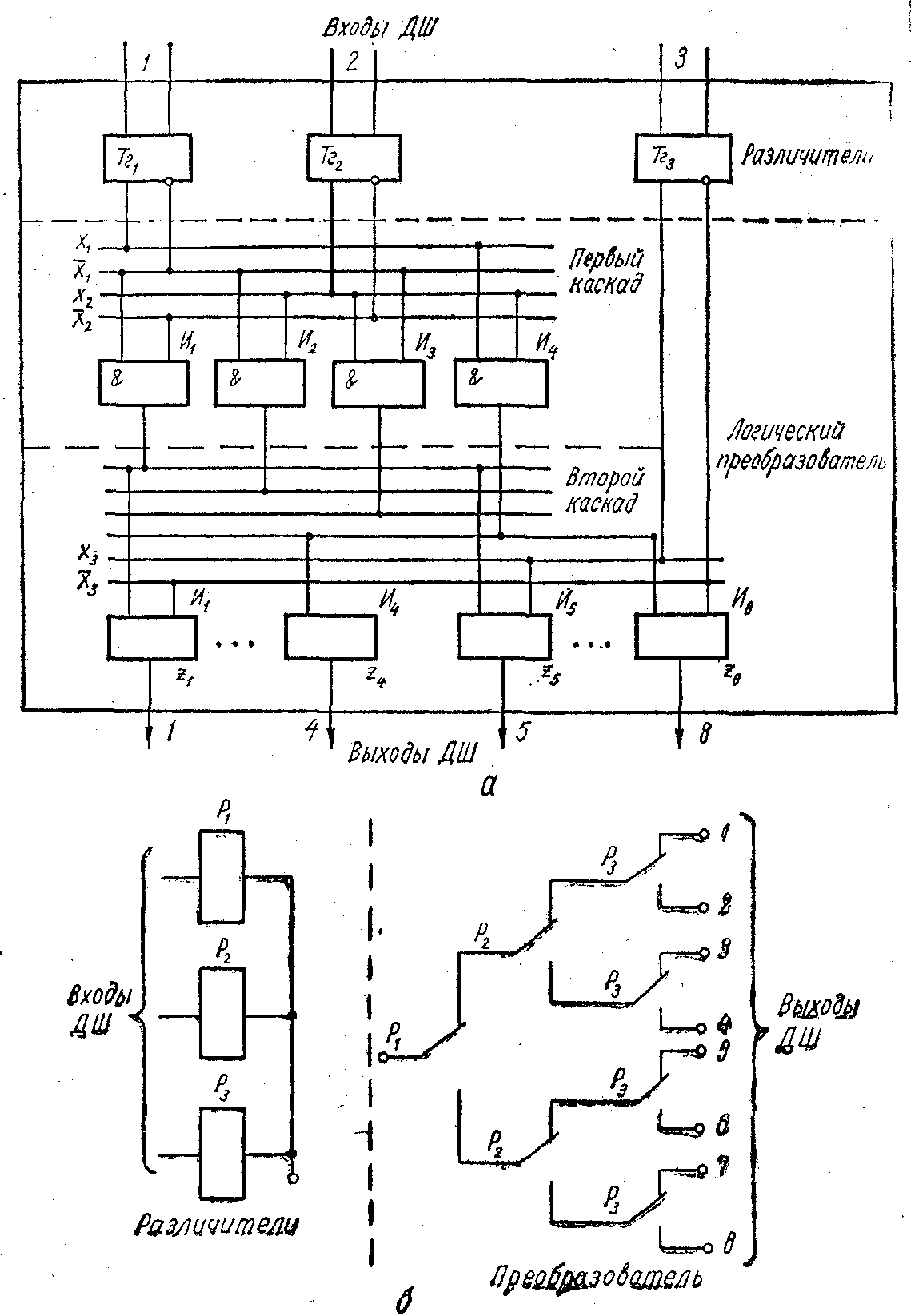
Рис. 1.3. Схема побудови пірамідального дешифратора:

а – електронного; б – релейно-контактного

Схеми з релейно-контактних елементів (мал. 3, б) будують аналогічно, за винятком першого каскаду. У цьому випадку розглянутий вище перший каскад складається з двох каскадів. Один з них містить два контакти (що замикає і що розмикає) реле, відповідних однією із змінних, наприклад х₁. Ці контакти, що об'єднуються часто в той, що перемикає, мають спільний вхід, на який подається одиничний сигнал; два їх виходи з'єднують з контактами реле, відповідного змінній х₁. Контакти цього реле утворюють другий каскад з числом виходів до чотирьох. Число каскадів для такої схеми рівне п. Слід зазначити, що схема мал. 3, б є конкретним різновидом схем, відомих під назвою «стандартного дерева».

Прямокутний дешифратор, як і пірамідальний, являє собою багатокаскадну схему, для якої кожна з вихідних функцій будь-якого каскаду являє собою кон'юнкцію. Відмітною особливістю прямокутного дешифратора є те, що вихідні функції будь-якого каскаду, крім першого, є кон'юнкціями функцій попереднього каскаду.

Розглянемо будову цього дешифратора, почавши з першого каскаду, реалізованого на схемах збігу. Всі задані п змінні розбивають на А груп з числом змінних в кожній групі, рівним φ. Мінімальне число таких груп А_мін = 2, а максимальне А_макс = Е(п/2) при φ = 2, де Е означає округлення у бік найближчого більшого цілого числа. Внаслідок такого округлення одна з груп може містити усього лише одну змінну. Для кожної з цих груп будують всі можливі конституанти, які називаються частковими, оскільки вони становлять лише частину вихідних конституант (п змінних). Часткові конституанти будують способом матричних схем. Таким чином, для будь-якої и-і групи, що містить φ змінних, часткова конституанта

де v - кількість змінних и – 1-ї групи.

У другому і подальших каскадах утворюються добутки часткових конституант, отриманих в різних групах попередніх каскадів, що дозволяє записати для v-го каскаду

де – часткова конституанта ψ-ї групи ν-го каскаду, якщо він не останній, або ω – конституанта, коли ν – останній каскад; – часткова конституанта и + t-ї групи ν – 1-го каскаду. Оскільки являє собою добуток всіх часткових конституант, то максимальне значення

(2)

де – кількість часткових конституант, утворених в и + t-й групі ν – 1-го каскаду. Функція являє собою часткову конституанту, якщо h – u < А_ν–1, тобто в тому випадку, якщо ця функція не охоплює часткові конституанти всіх А груп ν – 1-го каскаду. Такі часткові конституанти утворюються в окремих групах, число яких χ ≥ 2, Якщо ж h – u = А_ν–1, то охоплює часткові конституанти з всіх груп ν – 1-го каскаду. В цьому випадку и = 0, h = А_ν–1, χ = 1, ν = k (k – число каскадів), а вихідні функції, що реалізовуються

де – часткові конституанти j-ї групи k – 1-го каскаду. Кожна з них є частковою конституантою ψ_j змінних з п, а оскільки сума ψ_j = п, то – конституанта п змінних. Максимальне значення ω з урахуванням виразу (2)

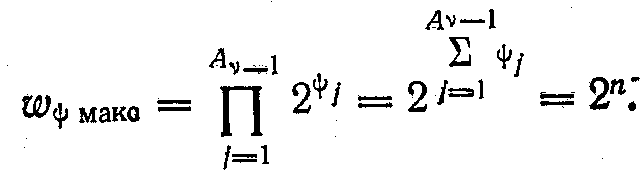
Як видно, часткові конституанти кожного подальшого проміжного каскаду, здійснюючи збіги часткових конституант попереднього каскаду, охоплюють все більше і більше число змінних; в останньому каскаді k таких змінних n.

Кожна функція являє собою h-входову схему збігу. Сукупність таких схем, що визначається максимальним значенням ω_ψ, є дешифратор для h – и змінних, і оскільки h – и < п, то таку дешифратор називається проміжним (ДШП).

Прямокутний дешифратор являє собою сполучені між собою описаним вище способом проміжні дешифратори першого і подальших каскадів. Схема такого з'єднання при використанні двовходових схем збігів в дешифраторі для чотирьох змінних показана на рис. 1.4.

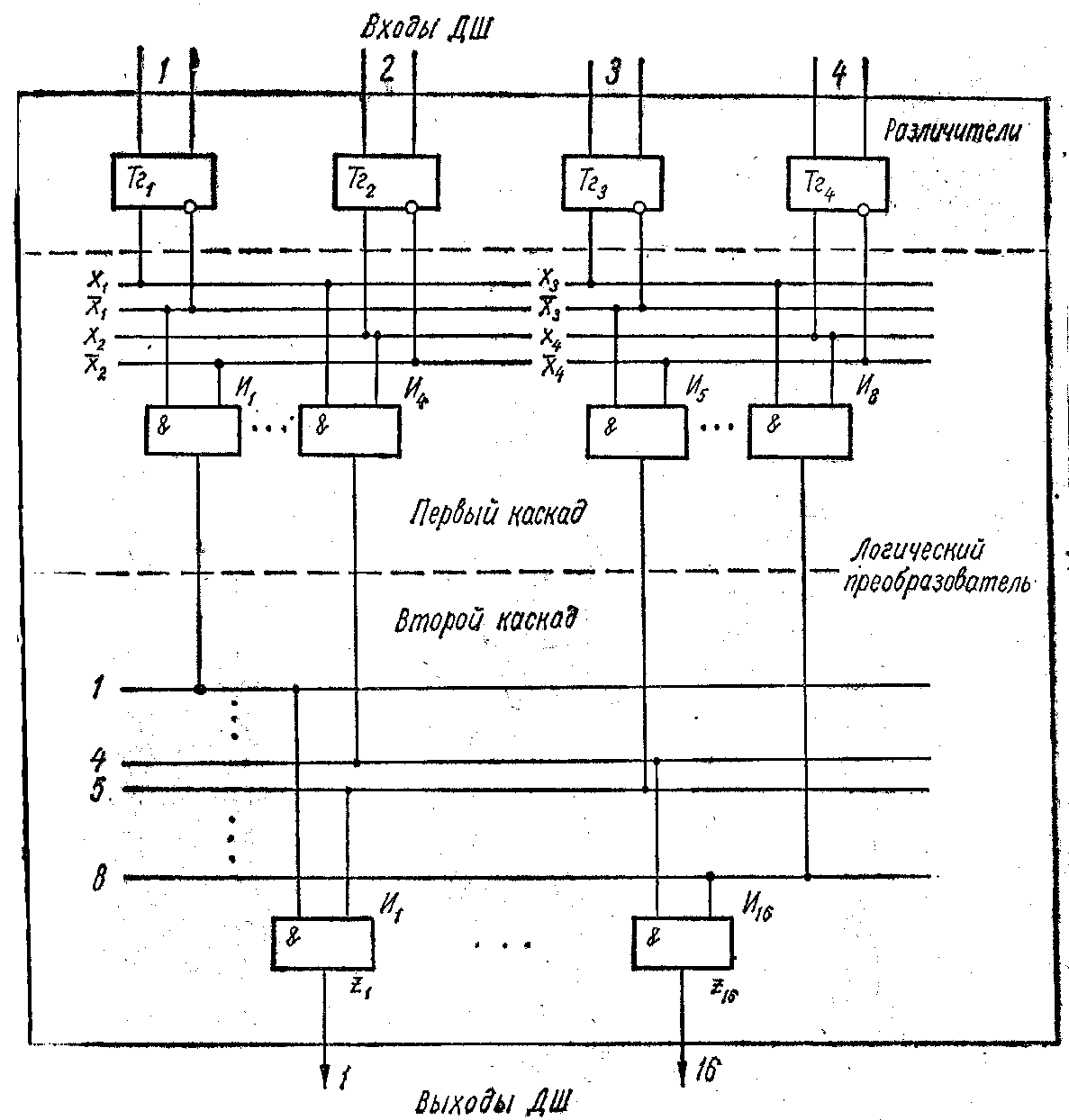
Рис. 1.4. Схема побудови прямокутного дешифратора

Істотної різниці між проміжними дешифраторами першого і подальших каскадів немає. У схемі рис. 1.5, наприклад, здійснює збіг сигналів двох груп по 16 виходів кожна, при цьому здійснюється збіг першого виходу першої групи з першим виходом другої групи, потім з другим виходом тієї ж групи і т. д. до утворення 16 схем збігів. Далі аналогічно здійснюється збіг другого виходу першої групи з всіма виходами другої групи і т. д. до отримання всіх 28 виходів. Проміжний дешифратор , здійснюючи збіг сигналів прямих і інверсних виходів Тг₁ і Тг₂, виконує аналогічну задачу, оскільки реалізовує схеми збігу для першого виходу Тг₁ і двох виходів Тг₂; далі для другого виходу Тг₁ з тими ж двома виходами Тг₂. Подібна задача вирішується при побудові проміжного дешифратора для трьох змінних.

Прямокутні дешифратори називають також багатоступінчастими, координатними та ін. Деяким різновидом прямокутних дешифраторів з двома каскадами є двополюсні діодні сітки.

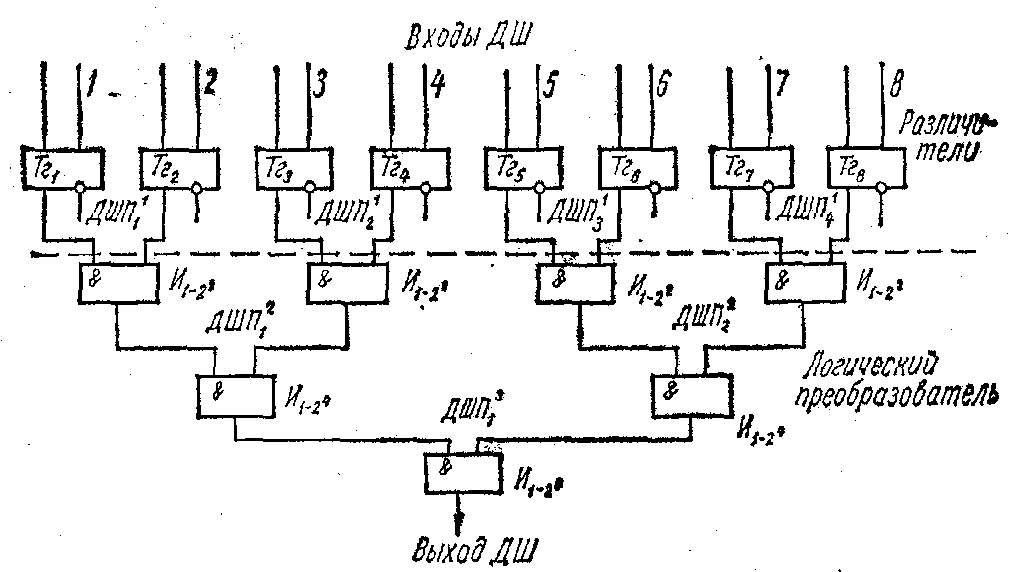
Рис. 1.5. Схема прямокутного дешифратора на 28 виходів

В ЕОМ дешифратор частіше застосовується для перетворення n-розрядного двійкового коду в унітарний код на 2п виходах (кожному n-розрядному двійковому коду на вході відповідає сигнал тільки на одному з 2п виходах). При цьому дешифратор реалізовує 2ⁿ функцій:

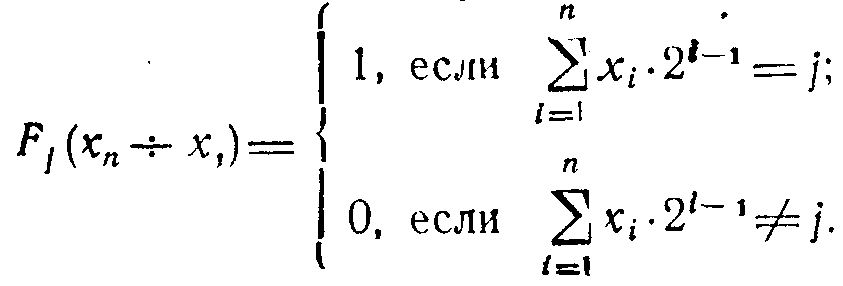
Кожна з функцій F_j(x_n …х₁) може бути записана у вигляді

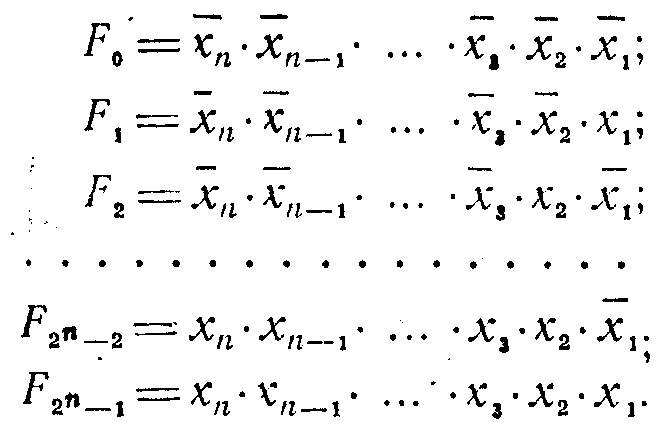
Такій системі рівнянь відповідає таблиця істинності (табл. 1.1).

Таблиця 1.1

xn	xn–1	…	x3	x2	x1	F0	F1	F2	…	F2n–3	F2n–2	F2n–1
0	0	…	0	0	0	1	0	0	…	0	0	0
0	0	…	0	0	1	0	1	0	…	0	0	0
0	0	…	0	1	0	0	0	1	…	0	0	0
…………………………………………………………………………………………
1	1	…	1	1	0	0	0	0	…	0	1	0
1	1	…	1	1	1	0	0	0	…	0	0	1

Сказане вище торкається повного дешифратора. На практиці зустрічаються неповні дешифратори, що реалізовують лише деякі з вихідних функцій F_j(x_n …х₁).

Способи побудови дешифраторів залежать від системи елементів, що використовується, розрядності вхідного коду, числа входів логічних схем, що використовується для побудови дешифратора.

В інтегральному виконанні широке поширення отримали лінійні (матричні) дешифратори. У них кожна функція F_j(x_n …х₁) реалізовується на окремому кон’юнкторі, що має п входів і 1 вихід. Схема лінійного дешифратора, що має п = 3 парафазних входи і 2^п = 8 виходів, і умовного графічного зображення дешифратора, наведені на рис. 1.6, а, б відповідно. На рис. 1.6, в наведено графічне умовне зображення дешифратора, де вхідні сигнали представляються однофазним кодом.

Крім лінійних дешифраторів існують каскадні (прямокутні і пірамідальні) дешифратори. Вони не набули поширення в інтегральних потенційних схемах внаслідок збільшення часу затримки поширення сигналу від входу до виходу. Цей параметр в порівнянні з матричною схемою збільшується в т раз, де т – число каскадів в схемі дешифратора.

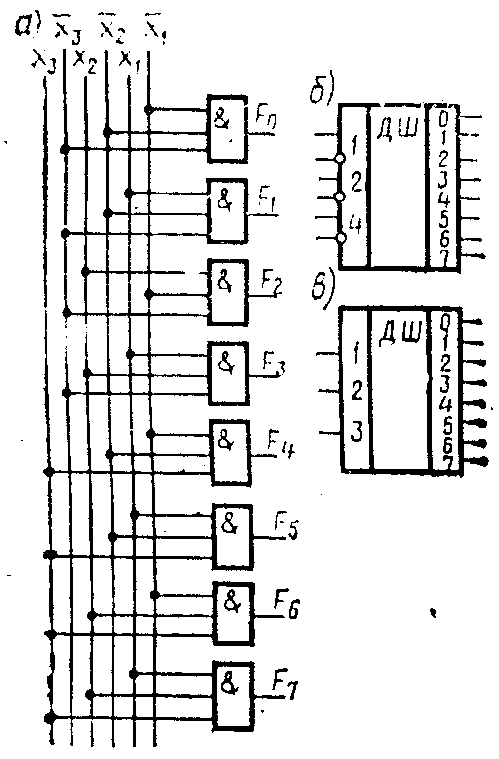
Рис. 1.6. Схема (а) лінійного дешифратора (п = 3 входи, 2^п = 8)

і його умовні графічні позначення (б, в)