Вариант 00 Образцы решения типовых задач контрольной работы

I. Продавец руководствуется одной из трех стратегий: назначить твердую цену 100 рублей за некоторый товар; установить первоначальную цену 100 рублей и затем сбавлять (в процессе торговли с покупателем) по 10 рублей вплоть до 60 рублей; назначить твердую цену 70 рублей. Покупатель выбирает одну из трех стратегий: купить товар за 100, 80, 60 рублей соответственно. Требуется:

а) составить платежную матрицу игры (элементами платежной матрицы является выручка продавца от продажи единицы товара);

б) найти решение игры в чистых стратегиях.

Решение.

Составим платежную матрицу игры . Для этого необходимо определить выручку продавца от продажи единицы товара.

Вычислим элементы первой строки платёжной матрицы: продавец устанавливает твердую цену 100 рублей. Покупатель принимает решение о приобретении товара: при использовании своей первой стратегии (элемент платежной матрицы ) он соглашается с ценой продавца ( =100), при использовании второй и третьей стратегий покупатель не согласен с ценой продавца, поэтому сделка не состоится ( = =0).

Аналогично найдем все остальные элементы платёжной матрицы:

=100 (цена 100 рублей устраивает обоих игроков);

=80 (продавец сбавляет цену товара от 100 до 80 рублей);

=60 (продавец сбавляет цену от 100 до 60 рублей);

=70 (продавец устанавливает цену 70 рублей, и эта цена устраивает покупателя);

=70 (цена 70 рублей выгодна и продавцу, и покупателю);

=60 (выставленная продавцом цена 70 рублей не устраивает покупателя, сделка не состоится).

В итоге платежная матрица примет вид:

Цена покупателя Цена продавца	100	80	60
100	100	0	0
от 100 до 60	100	80	60
70	70	70	0

Определим нижнюю и верхнюю цены игры. Для этого найдем:

1) минимальное из чисел 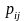в i-ой строке (i,j=1,2,3) платежной матрицы: ; числа выпишем рядом с платежной матрицей в виде добавочного столбца;

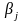2) максимальное из чисел в j-ом столбце (i,j=1,2,3) платежной матрицы: ; числа выпишем под платежной матрицей в виде добавочной строки.

Цена покупателя Цена продавца	100	80	60
100	100	0	0	0
от 100 до 60	100	80	60	60
70	70	70	0	0
	100	80	60

Находим минимальное из чисел : =60 (нижняя цена игры) и минимальное из чисел : =60 (верхняя цена игры).

Цена покупателя Цена продавца	100	80	60
100	100	0	0	0
от 100 до 60	100	80	6 0	60
70	70	70	0	0
	100	80	60	α=60, β=60

Поскольку α=β=60, игра имеет седловую точку, определяющую решение игры. Оптимальной стратегией для продавца является стратегия А₂ продажи товара по цене 60 рублей, оптимальной стратегией для покупателя является стратегия В₃ покупки товара по цене 60 рублей.

II. Сельскохозяйственное предприятие имеет возможность выращивать две культуры. Прибыль предприятия от реализации выращенной культуры зависит от объема полученной. Урожай первой культуры выше при сухой погоде, а второй — при более влажной. Состояние погоды в летний период можно рассматривать как следующие стратегии природы:

1. Лето жаркое сухое.

2. Лето жаркое влажное.

3. Лето теплое влажное.

4. Лето теплое сухое.

5. Лето прохладное сухое.

6. Лето прохладное влажное.

Стратегии предприятия:

1. Выращивать первую культуру.

2. Выращивать вторую культуру.

Предприятие считается игроком А, природа — игроком В. Расчеты прибыли предприятия в зависимости от состояния погоды сведены в следующую матрицу: (в млн. руб.). Требуется определить оптимальные стратегии поведения сельскохозяйственного предприятия.

Решение.

Рассматривая полученную ситуацию как матричную игру порядка 2x6, определим оптимальные стратегии предприятия - игрока А. Для определения нижней и верхней цены игры составим вспомогательную таблицу:

Bj Ai	B1	B2	B3	В4	В5	В6
A1	10	8	6	4	2	3	2
A2	1	2	4	3	12	6	1
	10	8	6	4	12	6	α=2, β=4

Поскольку α≠β, игра не имеет седловой точки, и решение следует искать в смешанных стратегиях. Для их нахождения воспользуемся графическим методом. Требуется найти

Определим средние выигрыши игрока А:

;

;

;

;

;

.

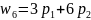Поскольку , преобразуем полученные равенства:

;

;

;

;

;

.

П остроим полученные прямые в системе координат (рисунок 1).

Рисунок 1

Далее строим нижнюю огибающую построенных прямых и отмечаем верхнюю точку М этой огибающей.

M

Рисунок 2

Точка М – точка пересечения прямых w₄ и w₆. Для определения координат точки М решим систему, составленную из уравнений указанных прямых:

.

Получим: , w= , .

Тем самым, цена игры  и оптимальная стратегия игрока А равны: = ,

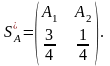
Использовать это решение сельскохозяйственное предприятие может следующим образом: на 75% имеющейся площади выращивать первую культуру, а на остальной выращивать вторую культуру, в этом случае прибыль предприятия составит 3,75 млн. рублей.

III. Две отрасли могут осуществлять капитальные вложения в три объекта. I-ая стратегия отрасли состоит в финансировании i-го объекта (i=1, 2, 3). Учитывая особенности вкладов и местные условия, прибыль первой отрасли выражается матрицей . Величина прибыли первой отрасли считается равной величине убытка второй отрасли. Найти оптимальные стратегии отраслей.

Решение.

Определим нижнюю и верхнюю цены игры:

Bj Ai	B1	B2	B3
A1	-2	0	1	-2
A2	1	-1	-1	-1
A3	-1	1	-1	-1
	1	1	1	α=-1, β=1

Так как =-1≠ =1, то игра не имеет седловой точки. Кроме того, в игре нет дублирующих и доминируемых стратегий.

Решаем игру путем решения пары двойственных задач линейного программирования.

Прибавим к каждому элементу платежной матрицы число 3, получим .

Математические модели пары двойственных задач линейного программирования будут выглядеть следующим образом:

Прямая (исходная) задача	Двойственная задача
Найти переменные х1, х2, х3, минимизирующие функцию F(x)=х1+х2+х3, при ограничениях:	Найти переменные у1, у2, у3, максимизирующие функцию Z(y)=y1+y2+y3, при ограничениях:

Существует множество компьютерных реализаций алгоритмов решения задач линейного программирования. Рассмотрим одну из них, входящую в электронные таблицы MS Excel 2007, – процедуру Поиск решения.

Для решения прямой задачи подготовим вначале исходные данные. На рисунке 1 приведен один из возможных вариантов представления данных на листе Excel.

В первую строку введем название задачи. В ячейки четвертой строки введем наименования искомых переменных. Ячейки А5, В5, С5 – это компоненты будущего оптимального плана, они – ячейки изменяемые (в нашей модели это неизвестные переменные), т.е., изменяя их, Поиск решения будет находить оптимальное значение целевой функции. Значения, которые первоначально вводят в эти ячейки, обычно нули (незаполненные клетки трактуются по умолчанию как содержащие нулевые значения).

В ячейке С7 вычислим значение целевой функции F(x)=х₁+х₂+х₃.

Рисунок 3

В ячейки А11:С13 введем коэффициенты при неизвестных в левых частях системы ограничений. В ячейках D11:D13 вычислим значения левых частях системы ограничений, используя функцию CУММПРОИЗВ. Присутствующие в формуле ячейки D11 знаки $ необязательны, но позволяют упростить процесс ввода: достаточно ввести формулу в D11, а затем протянуть ее по всему столбцу.

Рисунок 4

Сначала левые части системы ограничений и значение целевой функции автоматически оказываются равными 0. Далее заполняются столбцы «Знак» и «Правая часть».

Рисунок 5

Процедура Поиск решения позволяет автоматизировать перебор значений х_1, х_2, х₃, удовлетворяющих системе ограничений, до тех пор, пока не будет найдено оптимальное значение целевой функции. Прежде чем обратиться к процедуре, полезно выделить ячейку С7.

Для вызова процедуры следует войти в меню Данные, и там кликнуть мышью Поиск решения (если в Данных отсутствует Поиск решения, нужно предварительно установить эту надстройку; для этого с помощью кнопки Office следует открыть окно Параметры Excel, в котором в строке меню Надстройки нажать на кнопку Перейти к…, где и пометить Поиск решения).

При входе в Поиск решения на экране появится диалоговое окно (рисунок 6).

Рисунок 6

Поскольку исходная задача – задача на минимум, целевую ячейку устанавливаем равной минимальному значению. В качестве изменяемых ячеек выделяем А5:С5.

Рисунок 7

Для заполнения поля Ограничения нажмем кнопку Добавить, в появившемся окне в качестве Ссылок на ячейки выберем левые части системы ограничений, в качестве Ограничений – правые части. В итоге получим следующее заполнение поля Ограничения (рисунок 8).

Рисунок 8

Неотрицательность искомых переменных и линейность модели учтем в окне Параметры поиска решения (рисунок 9).

Рисунок 9

Затем следует нажать ОК, Выполнить, после чего появляется окно результата решения (рисунок 10).

Рисунок 10

Если в результате всех действий получено окно с сообщением Решение найдено, то Вам предоставляется возможность получения трех типов отчета, которые полезны при анализе модели на чувствительность. В данном примере достаточно сохранить найденное решение, нажав ОК. В результате получено решение прямой задачи линейного программирования (рисунок 11).

Рисунок 11

Если в результате решения задачи выдано окно с сообщением о невозможности нахождения решения (рисунок 12), это означает, что при оформлении задачи была допущена ошибка (не заполнены формулы для ограничений, неправильно установлен «флажок» максимизации/минимизации и т.д.).

Рисунок 12 Сообщение об ошибке

Таким образом, х₁=0,125, х₂=0,1875, х₃=0,0625, min F(X)=0,375.

Находим оптимальную смешанную стратегию игрока А: т

;

;

.

Поскольку в начале решения задачи ко всем элементам платежной матрицы было прибавлено число 3, то окончательной оптимальной ценой игры является = .

Следовательно, , .

Аналогичным образом найдем решение игры для игрока В.

Рисунок 13

Получаем y₁=0,125, y₂=0,125, y₃=0,125, max Z(Y)=0,375.

Определим вероятности применения своих активных стратегий игроком В:

;

;

.

Следовательно, , .

Полученные оптимальные стратегии игроки могут интерпретировать так: первая отрасль все свои капитальные вложения может распределить по объектам в долях, соответствующих вероятностям применения своих стратегий: в первый объект – 33%, во второй – 50%, в третий – 17% имеющихся средств; вторая отрасль — аналогично по отношению к своим капитальным вложениям: все объекты финансируются в равных долях (33,3%).

IV. Предприятие должно определить уровень выпуска продукции и предоставления услуг на некоторый период времени, так, чтобы удовлетворить потребности клиентов. Точная величина спроса на продукцию и услуги неизвестна, но ожидается, что в зависимости от соотношения сил на рынке товаров, действий конкурентов и погодных условий, спрос может принять одно из пяти возможных значений: П₁, П₂, П₃, П₄, П₅ изделий. Для каждого из возможных значений спроса существует наилучший уровень предложения А₁, А₂, А₃, А₄, А₅, с точки зрения возможной прибыли, отклонение от этих уровней связано с риском и может привести к дополнительным затратам либо из-за превышения предложения над спросам, либо из-за неполного удовлетворения спроса. Данная ситуация представлена в виде платежной матрицы игры (в у.е.). Требуется определить наилучшую стратегию поведения на рынке товаров и услуг:

а) в условиях неопределенности (γ =0,4 – показатель пессимизма);

б) в условиях риска, считая, что ранее проведенные маркетинговые исследования позволили определить возможные вероятности возникновения этих ситуаций, которые соответственно составили , , , , .

	q1=0,2	q2=0,3	q3=0,15	q4=0,15	q5=0,2
	П1	П2	П3	П4	П5
А1	58	19	25	97	16
А2	17	58	71	47	95
А3	52	88	20	105	76
А4	89	97	107	59	85
А5	55	15	41	68	74

Решение.

А) Для выбора наилучшей стратегии поведения на рынке товаров и услуг при неопределенной рыночной конъюнктуре существуют различные критерии, среди которых выделим критерии максимакса, Вальда, Гурвица и Сэвиджа. Считается, что оптимальной следует выбрать ту стратегию, которая будет предпочтительнее по нескольким критериям.

1 критерий (максимакса, крайнего оптимизма).

Определим величину максимакса в игре: =107. Выгодная стратегия А₄ может дать выигрыш предприятию в размере 107 у.е.

2 критерий (Вальда, крайнего пессимизма).

Дополним платёжную матрицу столбцом, каждый элемент которого представляет собой минимальное значение выигрыша в соответствующей стратегии предприятия: W_i = .

	П1	П2	П3	П4	П5	Wi
А1	58	19	25	97	16	16
А2	17	58	71	47	95	17
А3	52	88	20	105	76	20
А4	89	97	107	59	85	59
А5	55	15	41	68	74	15

Оптимальной по критерию считается та стратегия предприятия, при выборе которой минимальное значение выигрыша максимально:

W = max w_i=59.

Наилучшая стратегия А₄ дает выигрыш в размере 59 у.е.

3 критерий (пессимизма-оптимизма Гурвица).

Рассчитаем для каждой стратегии коэффициенты:

,

где – коэффициент пессимизма.

=64,6;

=63,8;

=71;

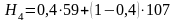=87,8;

=50,4.

Оптимальной по данному критерию считается стратегия, в которой значение H_i максимально:

H= max H_i=87,8.

Наилучшая стратегия А₄ дает выигрыш 87,8 у.е.

4 критерий (Сэвиджа).

Для определения оптимальной стратегии по данному критерию на основе платёжной матрицы составим матрицу рисков, каждый коэффициент которой (r_ij) определим по формуле:

,

где – максимальный элемент j – го столбца.

Дополним матрицу выигрышей дополнительной строкой

Матрица выигрышей	П1	П2	П3	П4	П5
А1	58	19	25	97	16
А2	17	58	71	47	95
А3	52	88	20	105	76
А4	89	97	107	59	85
А5	55	15	41	68	74
	89	97	107	105	95

и рассчитаем матрицу рисков:

Матрица рисков	П1	П2	П3	П4	П5
А1	89-58=31	97-19=78	107-25=82	105-97=8	95-16=79
А2	89-17=72	97-58=39	107-71=36	105-47=58	95-95=0
А3	89-52=37	97-88=9	107-20=87	105-105=0	95-76=19
А4	89-89=0	97-97=0	107-107=0	105-59=46	95-85=10
А5	89-55=34	97-15=82	107-41=66	105-68=37	95-74=21

Дополним матрицу рисков столбцом, содержащим максимальные значения коэффициентов r_ij по каждой из стратегий предприятия:

S_i = .

Матрица рисков	П1	П2	П3	П4	П5	Si
А1	31	78	82	8	79	82
А2	72	39	36	58	0	72
А3	37	9	87	0	19	87
А4	0	0	0	46	10	46
А5	34	82	66	37	21	82

Оптимальной по критерию считается та стратегия, в которой значение R_i минимально:

S = min S_i.

Наилучшая стратегия А₄ имеет риск 46 у.е.

5 критерий (принцип недостаточного основания Лапласа).

Для каждой стратегии предприятия рассчитаем средний выигрыш: .

Получим:

L₁ = (58+19+25+97+16)/5 = 43;

L₂ = (17+58+71+47+95)/5 = 57,6;

L₃ = (52+88+20+105+76)/5 = 68,2;

L₄ = (89+97+107+59+85)/5 = 87,4;

L₅ = (55+15+41+68+74)/5 = 50,6.

Наилучшая стратегия А₄ дает максимальный выигрыш в размере 87,4 у.е.

Ответ: по большинству критериев наилучшей стратегией предприятия является стратегия А₄.

Б) В условиях риска предприятие имеет информацию о вероятностях состояния спроса: =0,2, =0,3, =0,15, =0,15, =0,2.

Используем критерий максимального математического ожидания выигрыша Байеса. Рассчитаем математическое ожидание выигрыша предприятия при выборе соответствующей стратегии: ,где q_j –вероятность j-го состояния спроса:

38,8;

57,5;

70,75;

88,8;

46,65.

Оптимальной по данному критерию считается стратегия предприятия А₄, при выборе которой значение математического ожидания выигрыша максимально: =88,8.

V. Небольшая фирма (игрок А) намерена сбыть крупную партию товара на одном из двух рынков, контролируемых другой, более крупной фирмой (игрок В). Для этого оно может предпринять на одном из рынков соответствующие действия (например, развернуть рекламную кампанию). Господствующий на рынках игрок В может попытаться воспрепятствовать этому, предприняв на одном из двух рынков предупредительные меры. Игрок А, не встретивший на рынке препятствий, захватывает его; встретившись с сопротивлением – терпит поражение. Проникновение игрока А на первый рынок более выгодно для него, чем проникновение на второй, но борьба за первый рынок требует больших средств: победа игрока А на первом рынке принесет ему вдвое больший выигрыш, чем на втором, но зато поражение на первом рынке полностью его разоряет, а игрока В избавляет от конкурента. При поражении фирмы А на втором рынке на втором рынке ее потери будут не столь разорительны, но и победа принесет немного. Указанная игра задается матрицами выигрышей:

Решение.

Припишем стратегиям А₁, А₂ (В₁, В₂) вероятности р, 1-р (q, 1-q) соответственно:

Для того чтобы в биматричной игре , пара вероятностей определяла равновесную ситуацию, необходимо и достаточно одновременное выполнение следующих систем неравенств:

, (1)

, (2)

где , , , .

Заменяя в системах неравенств (1) и (2) величины С, α, D, β их конкретными значениями:

С=-10-2-1+(-1)=-14, α=-1-2=-3,

D=5-(-2)-(-1)+1=9, β=1-(-1)=2,

получаем:

(3)

(4)

Рассмотрим систему (3). Возможны следующие три случая:

1) р=1;

2) р=0;

3) 0<p<1.

Разберем каждый из случаев подробно.

1) Положим р=1, получим:

.

2) Положим р=0, получим:

.

3) Наконец, положив 0<p<1, получим:

.

Перенесем полученные сведения на чертеж. Введем на плоскости прямоугольную систему координат P0Q и выделим на ней единичный квадрат, соответствующий неравенствам , (рисунок 14).

Рисунок 14

Н анесем на чертеж множество решений случаев 1), 2), 3). Это множество состоит из трех прямолинейных участков – двух вертикальных лучей и одного горизонтального отрезка и представляет собой зигзаг. Нас будет интересовать только та его часть, которая попала в изображенный на рисунке единичный квадрат (см. рисунок ).

1

1

0

Рисунок 15

Обратимся к решению системы (4). Случаи

1) q=1;

2) q=0;

3) 0<q<1

приводят к результату:

1) ;

2) ;

3) .

Перенесем его на чертеж, получим второй зигзаг, но уже горизонтальный (рисунок 16).

1

1

0

Рисунок 16

Остается пересечь полученные данные. Общая точка построенных зигзагов – точка равновесия – имеет координаты .

Эта ситуация равновесия является ситуацией равновесия в смешанных стратегиях. Таким образом, оптимальными стратегиями по Нэшу являются:

Средний выигрыш игрока А равен:

.

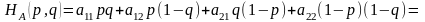
Средний выигрыш игрока В равен:

.

Содержание программы курса «Теория игр»

1. Основные понятия теории игр. Классификация игр. Платежная матрица игры. Максиминные и минимаксиные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Седловая точка.

2. Смешанные стратегии. Выигрыш-функция в смешанных стратегиях. Нижняя и верхняя цены игры в смешанных стратегиях. Доминирование стратегий. Решение матричных игр в смешанных стратегиях.

3. Критерии и свойства оптимальных решений матричных игр.

4. Разбиение матричной игры на подматрицы.

5. Изоморфные и аффинные преобразования матричных игр.

6. Аналитическое решение матричной игры 2×2.

7. Геометрическое решение матричных игр.

8. Решение матричных игр методом Шепли-Сноу.

9. Решение матричной игры приближенным методом Брауна-Робинсон.

10. Взаимосвязь матричных игр и линейного программирования.

11. Игры с природой. Принятие решение в условиях неопределенности и риска.

12. Планирование эксперимента в играх с природой.

13. Бесконечные антагонистические игры. Ситуация ε-равновесия, ε-седловые точки и ε-оптимальные стратегии.

14. Смешанные стратегии в бесконечных антагонистических играх.

15. Бесконечные антагонистические игры с непрерывной и выпуклой функциями выигрыша.

16. Одновременные игры преследования.

17. Определение бескоалиционной игры в нормальной форме.

18. Принципы оптимальности в бескоалиционных играх.

19. Смешанное расширение бескоалиционной игры.

20. Существование ситуации равновесия по Нэшу.

21. Свойства оптимальных стратегий в неантагонистических играх.

22. Равновесие в совместных смешанных стратегиях.

23. Многошаговые игры с полной информацией.

24. Ситуация абсолютного равновесия.

25. Основные функциональные уравнения.

26. Стратегии наказания.

27. Иерархические игры.

28. Многошаговые игры с неполной информацией.

29. Антагонистические дифференциальные игры с предписанной продолжительностью.

30. Многошаговые игры с полной информацией и бесконечным числом альтернатив.

31. Существование ситуации ε-равновесия в дифференциальных играх с предписанной продолжительностью.