4. Приложение 1.
Применение символического метода к расчету цепей переменного тока
Часть 1. Способы представления комплексных чисел
1. Основные понятия
При расчете цепей переменного тока основное применение получил симво-
лический метод. Этот метод по сравнению с другими резко упрощает расчет це-
пей переменного тока, т.к. позволяет использовать все соотношения и методы расчета цепей постоянного тока.
Суть метода состоит в том, что любую синусоидальную величину – напряже
ние, ток, мощность и т.п. можно представить в виде т.н. комплексного ( составно-
го ) числа.
2. Алгебраическая форма представления комплексных чисел
Комплексным числом или комплексом, называется число, состоящее из двух чисел ( частей ) – вещественного и мнимого.
Вещественным называется любое положительное или отрицательное число, например, + 5, - 28, и т.п. Обозначим вещественное число буквой “L”.
Мнимым называется число,
равное произведению вещественного
числа на квадратный корень из отрицательной
единицы, например, 8
,
- 20
,
и т.п.
Отрицательная единица называется мнимой и обозначается буквой «йот»:
j = (1 ).
Обозначим вещественное число в составе мнимого буквой “М”.
Тогда мнимое число можно записать так: j М. В таком случае, комплексное число А можно записать так:
А = L + j М ( 2 ).
Такая форма записи комплексного числа ( комплекса ) , представляющая собой алгебраическую сумму вещественной и мнимой частей, называется алгебраической.
Пример 1. Представить в алгебраической форме комплекс, вещественная часть которого равна 6, а мнимая 15.
Решение. А = 6 +j 15.
Кроме алгебраической формы, комплексное число можно представить еще тремя:
графической;
тригонометрической;
показательной.
Такое многообразие форм резко упрощает расчеты синусоидальных величин и их графическое изображение.
Поочередно рассмотрим графическую, тригонометрическую и показатель-
ную формы представления комплексных чисел.
3. Графическая форма представления комплексных чисел
Для графического представления комплексных чисел применяют прямо-
угольную систему координат. В обычной ( школьной ) системе координат вдоль осей «х» ( ось абсцисс ) и «y» ( ось ординат ) откладываются положительные или отрицательные вещественные числа.
В системе же координат, принятой в символическом методе, вдоль оси «х»
в виде отрезков откладывают действительные числа, а вдоль оси «у» – мнимые
( рис. 1 ).
Рис. 1. Система координат для графического изображения комплексных чисел
Поэтому ось абсцисс «х» называют осью вещественных величин или, для сокращения, вещественной осью.
Ось ординат называют осью мнимых величин или мнимой осью.
Саму же плоскость ( т.е. плоскость рисунка ), на которой изображают комплексные числа или величины, называют комплексной плоскостью.
В этой плоскости комплексное число А = L + j М изображено вектором А
( рис. 2 ), проекция которого на вещественную ось равна его вещественной части Re A = А' = L, а проекция на мнимую ось – мнимой части Im A = А" = М.
( Re – от англ. real – реальный, действительный, настоящий, Im – от англ.imaginary – нереальный, мнимый ).
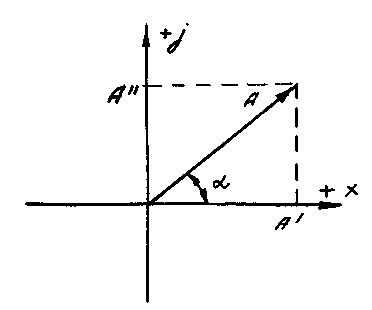
Рис. 2. Графическое представление комплексного числа
В этом случае число А можно записать так
А = А' + А" = Re A + j Im A ( 3 ) .
Используя графическое изображение числа А в комплексной плоскости, введем новые определения и получим некоторые важные соотношения:
1. длина вектора А называется модулем вектора и обозначается |A|.
По теореме Пифагора
|A| =
(
4 ) .
2. угол α, образованный вектором А и вещественной положительной полу-
осью, называется аргументом вектора А и определяется через его тангенс:
tg α = А" / А' = Im A / Re A ( 5 ).
Таким образом, для графического представления комплексного числа
А = А' + А" в виде вектора надо:
1. найти модуль вектора |A| по формуле ( 4 );
2. найти аргумент вектора tg α по формуле ( 5);
3. найти угол α из соотношения α = arc tg α;
в системе координат j ( х ) провести под углом α вспомогательную
прямую и на ней в определенном масштабе отложить отрезок, равный модулю вектора |A|.
Пример 2. Комплексное число А = 3 + j 4 представить в графической форме.
Решение:
модуль числа А
|A| =
=
=
=
5
аргумент числа
tg α = А" / А' = 4 / 3 = 1, 33
угол α = arc tg α = arc 1,33 = 53º 03' ≈ 53º
в системе координат j ( х ) проводим под углом α вспомогательную
прямую и на ней в масштабе μ = 1 А / см отложить отрезок длиной 5 см, равный модулю вектора |A| .
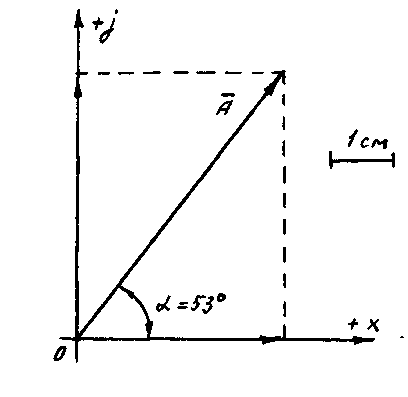
Рис. 3. Комплексное число А = 3 + j 4, представленное в графическом виде
( в виде вектора ).
При необходимости из рис. 2 можно найти другие тригонометрические функции:
sin α = А" / |А|, отсюда А" = |А| sin α ( 6 )
cos α = А' / |А|, отсюда А' = |А| cos α ( 7 ).
Выражения ( 6 ) и ( 7 ) будут использованы ниже при объяснении тригоно-
метрического изображения комплексных чисел.
Дополним тему «Графическая форма представления комплексных чисел»
исследованием роли мнимой единицы при графическом изображении комплексных
чисел.