
- •§18. Непрерывные случайные величины. Функция распределения случайной величины
- •Свойства функции распределения
- •§ 19. Плотность распределения
- •Вероятность попадания непрерывной случайной величины в заданный интервал
- •Нахождение функции распределения по известной плотности распределения
- •Свойства плотности распределения
- •§ 20. Числовые характеристики непрерывных случайных величин
- •Математическое ожидание
- •Дисперсия и среднее квадратическое отклонение непрерывной случайной величины
- •§21. Нормальный закон распределения (нормальное распределение)
- •Вероятностный смысл параметров a и
- •Нормальная кривая (кривая Гаусса)
- •Влияние параметров a и на форму и расположение нормальной кривой
- •Вероятность попадания в заданный интервал нормально распределенной случайной величины.
- •Вероятность заданного отклонения
- •Правило трех сигм
- •§22. Закон равномерной плотности. (Равномерное распределение) Определение, плотность распределения
- •§ 23. Показательное распределение
- •§ 24. Моменты распределения.
- •§ 25. Предельные теории вероятностей.
- •Неравенство Чебышева
- •Неравенство Чебышева
- •Частный случай теоремы Чебышева
- •Сущность теоремы Чебышева
- •Значение теоремы Чебышева для практики
- •Теорема Бернулли
- •Центральная предельная теорема.
§ 19. Плотность распределения
В качестве закона распределения, имеющего смысл только для непрерывных случайных величин, введем понятие плотности распределения.
Механическая интерпретация распределения вероятностей
Дискретная случайная величина: в точках x1, x2, ..., xi сосредоточены массы p1, p2, …, pi, причем суммы всех масс равны 1.
Н епрерывная
случайная величина: масса равная 1, не
сосредоточена в отдельных точках, а
непрерывно «размазана» по оси 0х с некой
плотностью (в общем случае неравномерной).
епрерывная
случайная величина: масса равная 1, не
сосредоточена в отдельных точках, а
непрерывно «размазана» по оси 0х с некой
плотностью (в общем случае неравномерной).
Средняя плотность на участке:
![]()
Опр. Плотностью распределения (или плотностью вероятности или просто плотностью) непрерывной случайной величины Х в точке х называется производная от функции распределении в этой точке
![]()
Плотность распределения f(x) иногда называют дифференциальной функцией распределения.
Г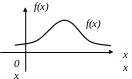 рафик
плотности распределения f(x)
называется кривой распределения.
рафик
плотности распределения f(x)
называется кривой распределения.
Вероятность попадания непрерывной случайной величины в заданный интервал
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (, ) равна определенному интегралу от плотности распределения, взятому в пределах от до
![]() .
.
Док-во. Воспользуемся формулой из §18:
![]() .
.
По формуле Ньютона-Лейбница:
![]() .
.
Отсюда: , что и требовалось доказать.
Г еометрически.
Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (,
) равна
площади криволинейной трапеции,
ограниченной кривой f(x),
осью 0х, прямыми x=,
x= .
еометрически.
Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (,
) равна
площади криволинейной трапеции,
ограниченной кривой f(x),
осью 0х, прямыми x=,
x= .
![]() .
.
Нахождение функции распределения по известной плотности распределения
Дано: f(x) – плотность распределения.
Найти: F(x) – функцию распределения.
По определению:
![]()
![]() .
.
![]() .
.
Свойства плотности распределения
Плотность распределения – неотрицательная функция
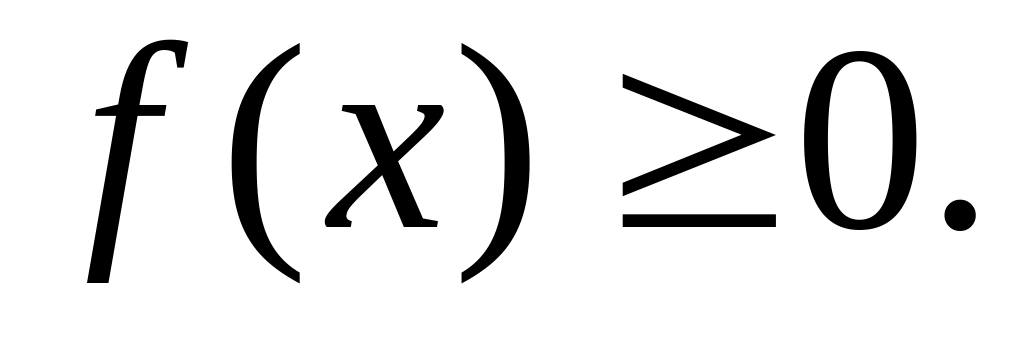
Док-во. Функция распределения F(x) – неубывающая функция, следовательно, ее производная f(x) = F’(x) – неотрицательная функция.
Несобственный интеграл от плотности распределения в пределах от - до + равен 1.
![]() .
.
Док-во.
![]() .
.
Частный случай. Если все возможные значения непрерывной случайной величины Х принадлежат интервалу (, ), то
![]() .
.
Геометрическая интерпретация свойств плотности распределения.
В
 ся
кривая распределения f(x)
лежит не ниже оси абсцисс.
ся
кривая распределения f(x)
лежит не ниже оси абсцисс.Полная площадь, ограниченная кривой распределения f(x) и осью абсцисс, равна 1.
Механическая интерпретация.
![]() .
.
![]() вероятность
попадания Х на участок
вероятность
попадания Х на участок
![]() ,
интерпретируется как масса, приходящая
на участок
.
,
интерпретируется как масса, приходящая
на участок
.
![]() средняя
плотность на участке
.
средняя
плотность на участке
.
![]() плотность
массы в точке
.
плотность
массы в точке
.
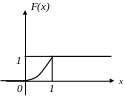
Пример. Дана функция распределения непрерывной случайной величины Х.
![]()
а) найти плотность распределения f(x);
б) графики F(x) и f(x);
в) найти вероятность попадания Х в (0,25; 0,5); (0,5; 0,2).
Решение.
а)
![]()

б)
в)
![]() (1-й способ)
(1-й способ)
![]() (2-й способ).
(2-й способ).
![]()
