Неравенство Чебышева

Пусть X – случайная величина, M(X) – математическое ожидание, D(X) – дисперсия. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа E есть число, не меньше, чем

без доказательства

Неравенство Чебышева

Пусть имеется последовательность случайных величин

Опр. Говорят, что последовательность случайных величин X_n сходится по вероятности к неслучайной величине a, если при сколь угодно малом положительном числе вероятность неравенства с увеличением n неограниченно приближается к единице.

или

Различия между сходимостью в смысле обычного математического анализа (1) и сходимостью по вероятности (2) в следующем:

(1)

(2) для отдельных значений n неравенство может не выполняться.

Закон больших чисел устанавливает условия сходимости по вероятности (тех или иных) случайных величин к определенным постоянным.

Теорема Чебышева (одна из важных форм закона больших чисел)

Если попарно независимые случайные величины, причем их дисперсии равномерно ограничены (не превышают постоянного числа c), то

или

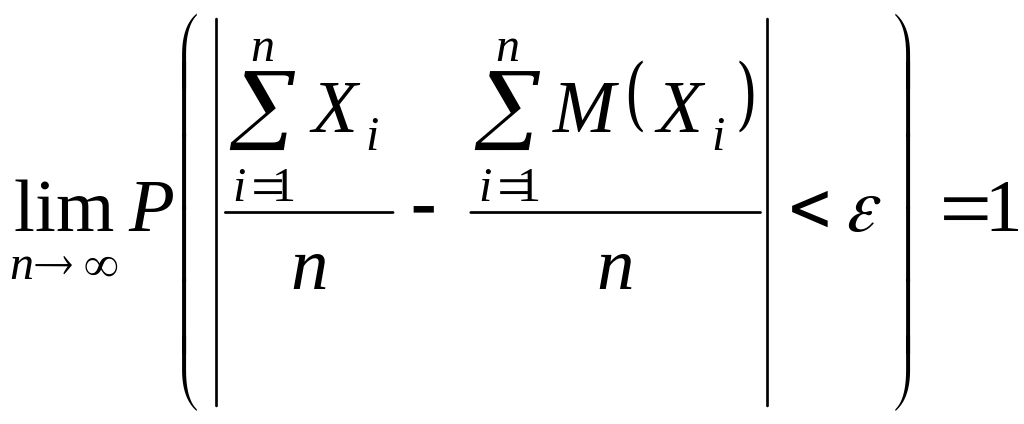
Док-во:

Обозначим

Применим к случайной величине неравенство Чебышева

*

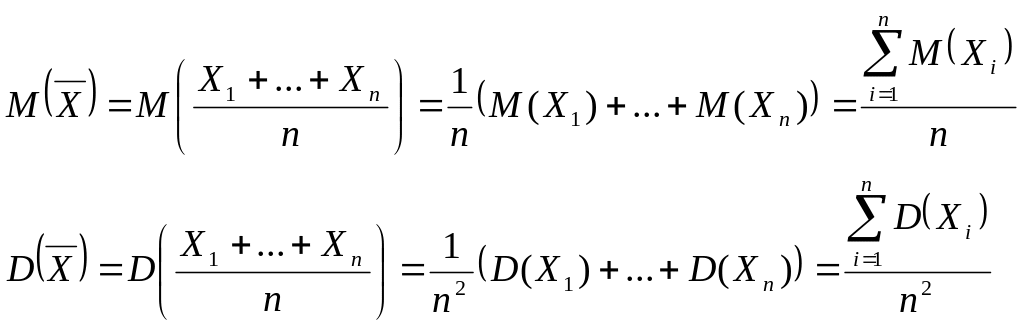
По условию значит

Подставим в (*)

Перейдем к при

Т.к. вероятность не может быть >1, то , что и требовалось доказать.

Частный случай теоремы Чебышева

Если попарно независимые случайные величины, имеющие одно и то же математическое ожидание a, и если дисперсии этих величин равномерно ограничены, то

или

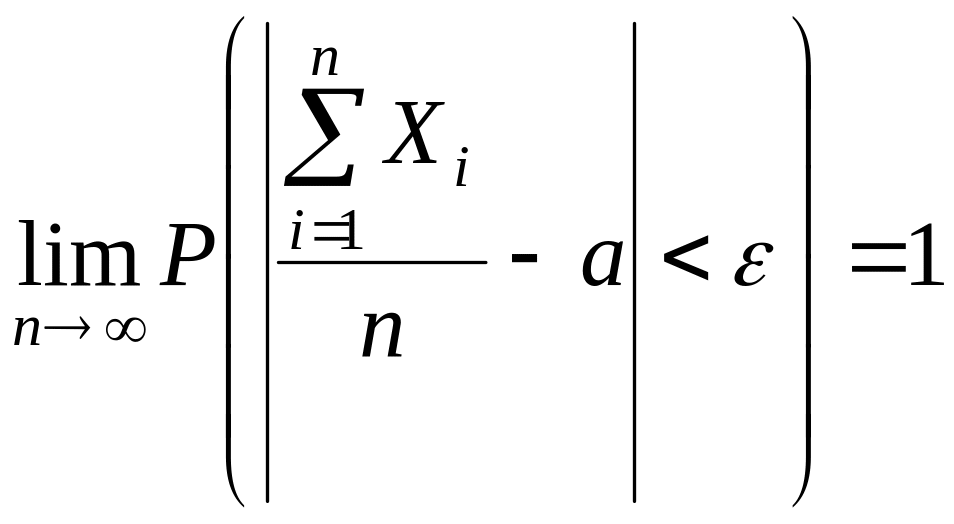
Сущность теоремы Чебышева

Хотя отдельные независимые случайные величины могут принимать значения далекие от своих математических ожиданий, среднее же арифметическое большого числа случайных величин с большой вероятностью принимает значения, близкие к среднему арифметическому их математических ожиданий, т.е. к постоянному числу. [ Нельзя предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть какое значение примет их среднее арифметическое].

Значит среднее арифметическое достаточно большого числа независимых случайных величин, дисперсии которых равномерно ограничены, утрачивает характер случайной величины.

Теорема Чебышева справедлива и для дискретной и для непрерывной случайной величины.

Значение теоремы Чебышева для практики

Для измерения некоторой физической величины делают несколько замеров и их среднее арифметическое принимают в качестве искомого результата. Теорема Чебышева указывает условия, при которых это справедливо.

Рассмотрим результаты каждого замера как случайные величины .

1. попарно независимы; выполняется, если результат ^го замера не зависит от остальных.

2. имеют одно и то же математическое ожидание; выполняется, если измерения производятся без систематических (одного знака) ошибок.

3. дисперсии равномерно ограничены; выполняется, если прибор обеспечивает определенную точность измерений. Тогда, по теореме Чебышева, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отличается от истинного значения измеряемой величины.

На теореме Чебышева основан выборочный метод, суть которого в том, что по небольшой выборке судят о всей совокупности исследуемых объектов.