Теорема Бернулли

Пусть производится n независимых испытаний, в каждом из которых событие A появляется с вероятностью p (а не появляется с вероятностью q=1-p).

P(A)=p; P*(A)=m/n – относительная частота (частота)

Теорема: При неограниченном увеличении числа испытаний n частота события A сходится по вероятности к p.

или

Док-во.

Обозначим X₁ – число появлений события A в 1^ом испытании

X₂ – число появлений события A в 2^ом испытании

X_n – число появлений события A в n^ом испытании

Законы распределения одинаковы, а именно

Xi	0	1
p	q	p

X_i=0, – событие А не появилось в i^ом испытании

X_i=1, – событие А появилось в i^ом испытании i=1, 2,..., n

M(X_i)=p; D(X_i)=0q+1p-p²=p-p²=pq

X₁+ X₂ +...+ X_n=m – столько раз появилось A в n испытаниях.

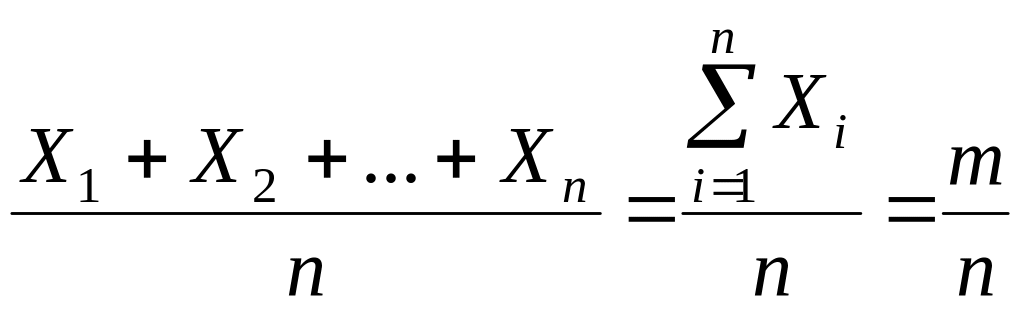– относительная частота события A.

Применим частный случай теоремы Чебышева

1) – попарно независимые (вып-ся)

2) имеют одно и то же математическое ожидание, M(X_i )=p,

3) дисперсии равномерно ограничены

Д ействительно: D(X_i) = pq = p – p², 0<p<1, i =1, 2,..., n

D’(X_i)=1 – 2p, D’(X_i)=0  p = ½

Единственный экстремум, max  при p = ½ наибольшее значение

D_{наиб .}= ½  ½= ¼ , D(X_i) ¼ – равномерно ограничена. Тогда, по теореме Чебышева

или , что и требовалось доказать.

Теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности.

Центральная предельная теорема.

Согласно центральной предельной теоремы закон распределения суммы достаточно большого числа независимых (или слабо зависимых) слагаемых, каждое из которых в отдельности мало влияет на сумму, сколь угодно близкую к нормальному.

Опр. Случайной величиной называют нормированной суммой (центрированной случайной величиной)

Теорема 1. (Теорема Линдеберга - Леви)

Если – независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m и дисперсией ², то при неограниченном увеличении n закон нормированной суммы Z_n сходится по вероятности к нормальному закону с плотностью вероятностей (m = 0,  = 1). Без доказательства.

Замечание. В условиях теоремы при увеличении n закон распределения суммы также не неограниченно приближается к нормальному (но с плотностью другого вида). Центральная предельная теорема справедлива и для неодинаково распределенных случайных величин.

Теорема 2. (теорема Ляпунова)

Если – независимые случайные величины, имеющие математические ожидания m₁, … , m_n и дисперсии D₁, … , D_n причем

(*)

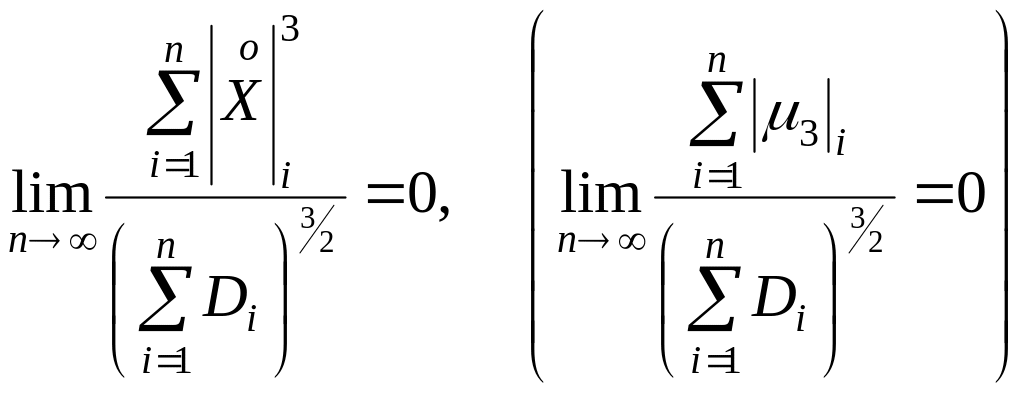где

то при неограниченном увеличении n закон распределения нормированной суммы Z_n сходится по вероятности к нормальному закону. С плотностью вероятностей (без доказательства)

Другая формулировка: В условиях теоремы при n закон распределения случайной величины неограниченно приближается к нормальному. Смысл условия (*) состоит в том, что действие  слагаемого невелико по сравнению с суммарным действием всех.

Практически центральной предельной теоремой можно пользоваться и в случае небольшого числа слагаемых (порядка 10): если суммируются случайные величины, сравнимые по своему рассеиванию.

Пример

1. Производится измерение некоторой величины a, суммарная ошибка измерения является случайной величиной, распределенной по нормальному закону (воздействует много факторов, порождающих малую ошибку X_i)