Мінором деякого порядку

являється визначник, який отримують шляхом умовного закреслення рядка та стовпця, на перетині яких знаходиться цей елемент:

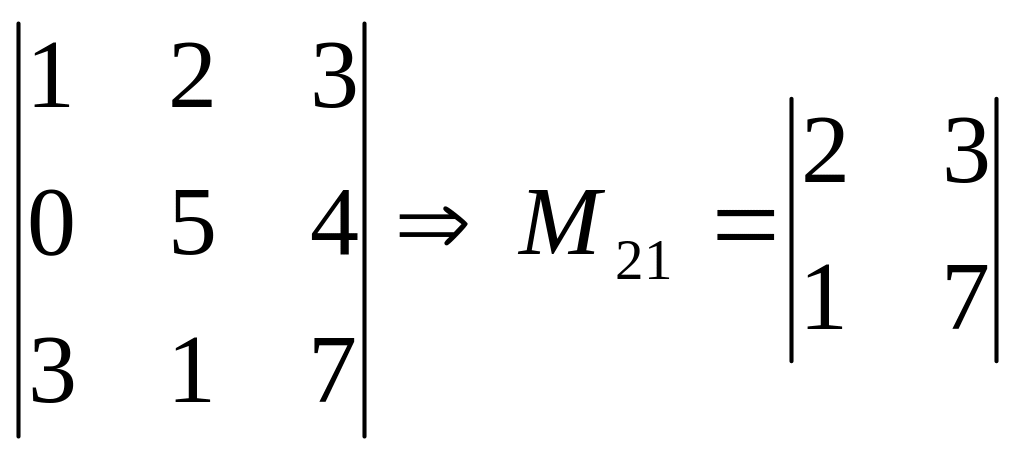
Алгебрагічним доповненням

Деякого елемента визначника називається мінор цього елемента, помножений на коефіцієнт (-1)^р, де Р – це сума номерів рядка та стовпця, на перетині яких розміщений цей елемент:

Аij=(-1)^i+j_*M_ij

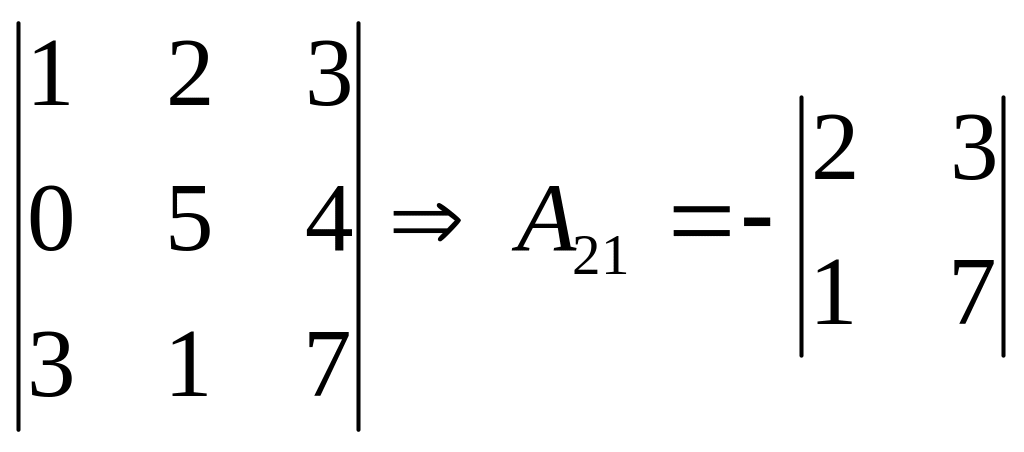
Транспонування матриць

Транспонування матриці називається заміна рядків цієї матриці її стовпцями із збереженням їх порядку.

Матриця, отримана таким чином з матриці А називається транспонованою по відношенню до А і позначається [А]^т. Для елементів транспонованих матриць виконується умова аij— аjj^T . Для симетричної матриці виконуються умови А^т =А.

Функція fx - категорія Посилання на масиви -ТРАНСП(масив)- - розповсюдити на порядок mxn - - [F2]-{Ctrl-Shift-Enter] ---- повертає вертикальний діапазон комірок у вигляді горизонтального і навпаки.

Обернена матриця

Квадратна матриця [А]називається оберненою по відношенню до матриці А того ж порядку, якщо справедлива

Теорема: Для того, щоб матриця [А]^-1 мала зворотну, необхідно і достатньо, щоб вона була не виродженою або невласною, тобто det А ≠ 0.

Якщо det А = 0, матриця називається виродженою або особливою.

Порядок обчислення оберненої матриці:

• обчислюється визначник матриці (det А ≠ 0);

• обчислюється допоміжна (союзна) матриця (алгебраїчні доповнення кожного елементу матриці з урахуванням знаку);

• транспонується допоміжна матриця;

• обчислюється обернена за формулою А^-1=1/detA * А^т

Перевірка: А^-1*А = Е (одинична матриця) + [F2]-{Ctrl-Shift-Enter]

А = Е / А^-1 = Е*А

А^-1 = Е / А

Функція fx - категорія Математичні – МОБР(масив) – розповсюдити на порядок mxn - - [F2]-{Ctrl-Shift-Enter] ---- повертає діапазон комірок

Обернена матриця обчислюється по правилах:

1. Обчислюється визначник матриці А.

2. Обчислюється союзна матриця, тобто матриця. складена з алгебраїчних доповнень елементів аіj матриці А:

А₁₁ А₁₂ А_1n

[ А*] = А₂₁ А₂₂ А_2n

А_m1 А_m2 А_mn

3) Транспонується союзна матриця

А₁₁ А₁₂ А_1n

[ А] = А₂₁ А₂₂ А_2n

А_m1 А_m2 А_mn

4) Обчислюється зворотна матриця:

Перевірка: А^-1*А = Е

Визначник

Функція fx - категорія Математичні – МОПРЕД(масив) – повертає одиничне значення

Визначником другого порядку

відповідної матриці А, називається число

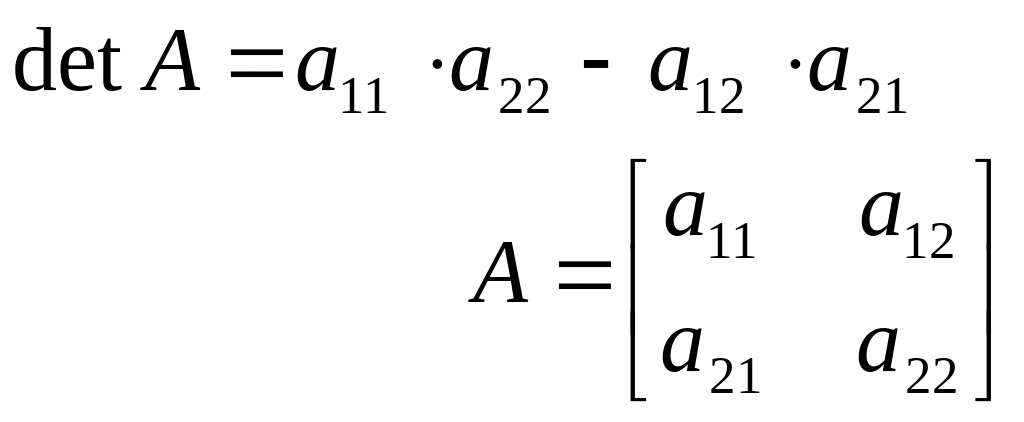
побічна і головна діагональ

Визначники третього порядку

можна обчислювати за правилом трикутника відповідної матриці А:

D_A = a₁₁ ^. a₂₂ ^. a₃₃ + a₁₂ ^. a₂₃ ^. a₃₁ + a₁₃ ^. a₂₁ ^. a₃₂ +-a₁₃ ^. a₂₂ ^. a₃₁ – a₁₁ ^. a₂₃ ^. a₃₂ – a₁₂ ^. a₂₁ ^. a₃₃ і позначається

а₁₁ а₁₂ а₁₃

[ А] = а₂₁ а₂₂ а₂₃

а₃₁ а₃₂ а₃₃

Властивості визначників:

1. Величина визначника не зміниться, якщо його рядки замінити стовпцями, не міняючи їх порядку, тобто величина визначника не міняється при транспонуванні, тобто

2. Перестановка двох стовпців або двох рядків визначника рівно цільна множенню його на (-1).

3. Якщо визначник має два однакові стовпці або два однакові рядки, то він рівний нулю.

4. Множення всіх елементів одного стовпця або одного рядка визначника на будь-яке число X рівноцінне множенню визначника на це число Х.

5. Якщо всі елементи деякого стовпця або деякого рядка визначника рівні нулю, то і сам визначник рівний нулю.

6. Якщо елементи двох стовпців або двох рядків визначника пропорційні, то визначник рівний нулю.

7. Якщо кожен елемент n-го стовпця () є сумою двох доданків, то визначник може бути представлений у вигляді суми двох визначників, з яких один в n-ому стовпці (m-ому рядку) має перші із згаданих доданків, а інший - другі; елементи, що стоять на основних місцях, у всіх трьох визначників одні і ті ж.

8. Якщо до елементів деякого стовпця (рядка) визначника додати відповідні елементи іншого стовпця (рядка), помножені на будь-який загальний множник X, то величина визначника не зміниться.

9. Визначник рівний сумі добутків якого-небудь стовпця або рядка на їх алгебраїчне доповнення.

10. Запис визначника у вигляді із записаної рівності називаються розкладання його по елементах деякого стовпця або деякого рядка. (Теорема Лапласа).

11. Сума добутків елементів якого-небудь стовпця або якого-небудь рядка визначника на алгебраїчне доповнення відповідних елементів іншого стовпця або іншого рядка рівна нулю.

Використовуючи властивості визначників можна способом перетворення визначника прийти до матриці порядку 2х2 та обчислити її визначник по правилу прямокутника.

Рангом матриці А називається найбільший порядок, який може мати її мінор, відмінний від нуля (г (А)).

Для визначення рангу матриці слід розглядати весь її мінор найменшого порядку. Якщо хоч один з них відмінний від нуля, то слід переходити до розгляду мінору вищого порядку.

Для визначення рангу матриці можна використовувати звичайні жорданові виключення або обчислювати на основі еквівалентності матриць і елементарних перетворень над ними.

Якщо матриця А отримана з матриці В шляхом проведення кінцевого числа елементарних перетворень, то матриця А еквівалентна матриці В.

rang(A)= rang(B)

Для обчислення рангу матриці її слід привести до трапецієвидної форми. При цьому матриця має трапецієвидну форму якщо:

• всі елементи, що стоять нижче діагональних, рівні нулю, а діагональні елементи a₁₁, a₂₂ ., a_nn відмінні від 0;

• всі елементи останніх m-р рядків обернені в нуль.

Початкова матриця приводиться до трапецієвидної форми за допомогою алгоритму Гауса:

Виконується складання першого рядка, заздалегідь помноженого на деякий множник, з іншим рядком. Слід добитися, щоб всі елементи, що стоять нижче за елемент а₁₁ перетворилися на нуль. Аналогічно добиваються, щоб всі елементи, що стоять нижче а₂₂ перетворились в нуль.

Теорема. Рядки матриці Г1 Г2, Г3... Гn лінійно залежні тоді і тільки тоді, коли хоч би один з них можна виразити через останні або коли один з них можна представити як лінійну комбінацію останніх.

Для стовпців теорема аналогічна.

Слідство з теореми. Рядки ГІ, Г2, Г3 ... Гn називаються лінійно незалежними, якщо їх лінійна комбінація обертає в нуль рядок, коли всі коефіцієнти _i= 0, i = 1,n

Число лінійно незалежних рядків матриці рівне числу лінійно незалежних стовпців рівні рангу матриці.

Теорема: Визначник матриці рівний нулю, якщо його рядки (стовпці) лінійно незалежні.

Якщо ранг матриці рівний р, то мінор будь-якого порядку р, відмінний від нуля, називається базисним мінором; рядок і стовпець, з яких складений базисний мінор, називається базисним.

Ранг матриці не міняється при виконанні елементарних перетворень:

• заміна рядків стовпцями;

• перестановка рядків матриці;

• викреслювання рядка, елементи якого рівні нулю;

• множення якого-небудь рядка на деяке число;

• збільшення до елементів одного рядка відповідних елементів іншого рядка.