Системи лінійних рівнянь алгебри

Систему рівняння вигляду:

називають системою n-лінійних рівнянь з n-залежними.

Коефіцієнти рівнянь, записані у вигляді матриці А:

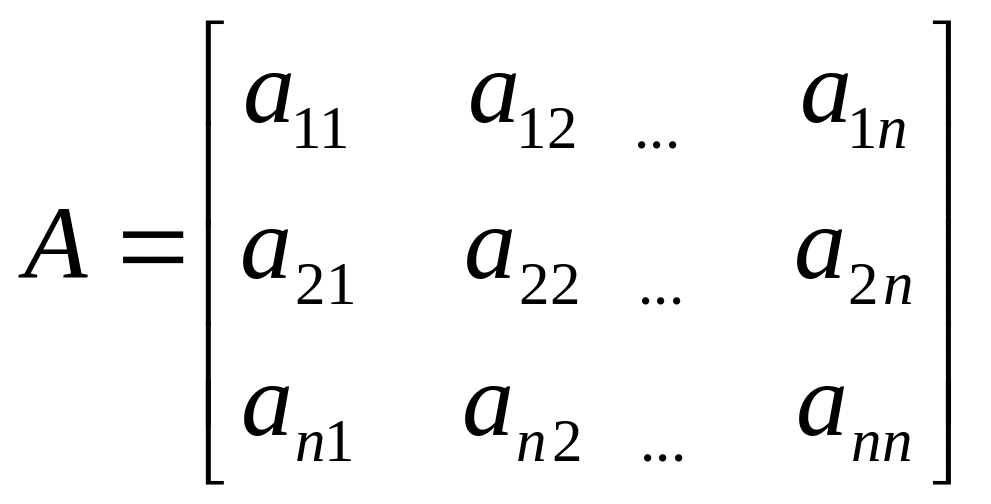
називають матрицею системи, а її визначника називають визначником системи.

Числа b_1, b_2, b_n називаються вільними числами.

Матриці системи, доповнені справа стовпцем вільних елементів, називаються розширеною матрицею системи

Якщо всі коефіцієнти стовпця вільних елементів обертаються в нуль, то система лінійних рівнянь алгебри називається однорідною.

Сукупність чисел X1=λ1, X2= λ 2 , Xn= λ n, називається рішенням системи лінійних рівнянь алгебри, якщо кожне рівняння системи обертається в тотожність після підстановки в нього чисел λ i замість відповідних Xiі = 1,n.

Система лінійних рівнянь алгебри, що має хоч би одне рішення, називається сумісною, а якщо немає рішень - несумісною.

Сумісна система лінійних рівнянь алгебри називається визначеною, якщо вона має одне рішення і невизначеною, якщо має безліч рішень.

Метод Крамера

Хай дана система лінійних рівнянь алгебри mхn:

(1)

Якщо визначник матриці системи (1) не рівний нулю, то лінійне рівняння має рішення і при тому єдине. Обчислення системи лінійних рівнянь алгебри при цьому визначається по формулах Крамера:

X _j =∆j / ∆ j=1,n,

де ∆ - визначник матриці системи.

∆j – визначник, що отримується з визначника матриці системи, якщо в ньому замінити j-й стовпець стовпцем вільних еементів.

Xi – рішення системи лінійних рівнянь алгебри.

Матричний метод рішення системи лінійних рівнянь алгебри

Хай визначник системи відмінний від нуля. Позначимо матрицю-стовпець з невідомих через Х, а матрицю-стовпець з вільних членів через В:

Тоді, згідно правилу множення матриць, отримаємо:

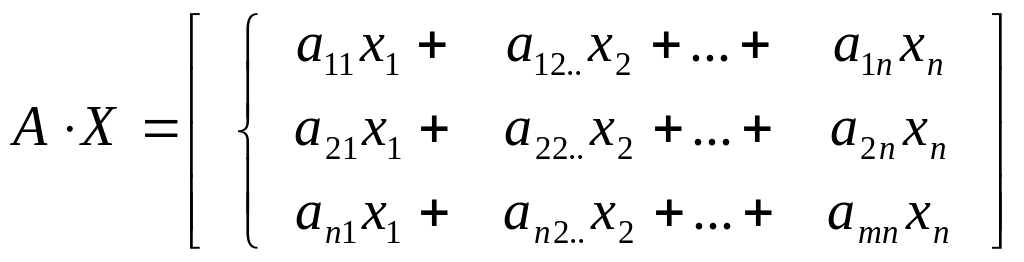
Використовуючи визначення рівності матриць, дану систему (1) можна записати таким чином:

А*Х=В - матричне рівняння (2)

Оскільки по умові |A|≠0, то для матриці А існує зворотна матриця А^-1:

А^-1*(А*Х)= А^-1*В

Але, оскільки А^-1*А=Е і Е*Х=Х, то отримуємо рішення матричного рівняння у вигляді:

Х= А^-1*В

Дослідження систем лінійних рівнянь алгебри

При рішенні системи лінійних рівнянь алгебри може статися, що визначник системи рівний нулю або число рівнянь не рівне числу невідомих. Тому рішенню системи лінійних рівнянь алгебри повинно передувати дослідження, які виконуються в наступному порядку:

1. досліджувати чи є система рівнянь сумісною або несумісною, тобто чи має вона взагалі рішення;

2. якщо система сумісна то досліджувати чи є система рівнянь визначеною, тобто чи має вона єдине рішення або такі рішень багато;

3. якщо система сумісна і визначена знайти її єдине рішення;

4. якщо система сумісна і не визначена, то описати сукупність рішень системи.

Теорема Кронеккера-капелі

Позначимо через А матрицю системи, через С - розширену матрицю.

Система m лінійних рівнянь з n незалежними змінними сумісна тоді, коли ранг матриці А рівний рангу розширеної матриці С. Якщо ранг розширеної матриці рівний рангу матриці А і числу невідомих, тобто

r(A)= r(C)= n

то система має єдине рішення.

Якщо ранг розширеної матриці менше числа невідомих:

г (А) - г (С) <n

то система має нескінченну безліч рішень.

Якщо ранг матриці А не рівний рангу матриці С, то система лінійних рівнянь алгебри несумісна.

Звичайні Жорданові виключення.

Розглянемо систему m лінійних функцій з n невідомими

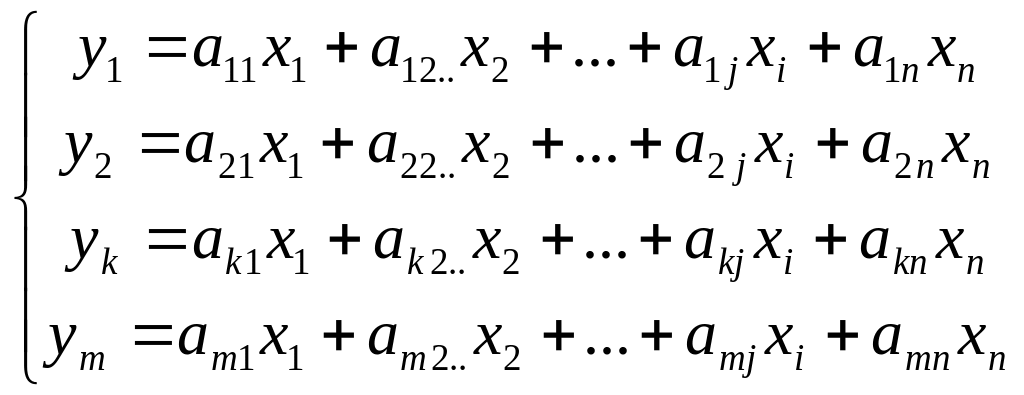
Х1, Х2, Х3, ..., Хn - незалежні змінні;

УІ, У2, У3, …, У _m - залежні змінні.

Цю систему можна записати скорочено:

де i = 1, m

Представимо систему (1) у вигляді таблиці:

	x1	x2	…	xis	..	xn
y1	a11	a12	...	als	...	a1n
y2	a21	a22	...	a2s	...	а2n
Yk	ak1	aks	...	aks	...	akn
ym	am1	am2	...	ams	...	amn

Така таблиця називається жордановою. Перехід від цієї таблиці до системи (1) здійснюється таким чином: елементи a_Kj (k=l,m) к-го рядка множаться на відповідні незалежні змінні x_j (j=1,n), які розміщені у верхньому рядку. Отримані таким чином добутки складаються і прирівнюються до залежної у_k (k=1,m).

Систему (1) необхідно перетворити так, щоб залежна змінна у_k після перетворення стала незалежною, а незалежна змінна x_s - залежною. Така операція називається одним кроком Жорданових виключень. При цьому a_ks -називаєтся ключовим (вирішуючим) елементом; k-й рядок називається вирішуючим рядком, s-й стовпець - називається ключовим (вирішуючим) стовпцем.

Один крок звичайних Жорданових виключень з вирішуючим (дозволяючим) елементом a_ks зручно розбити на наступні операції:

1. вирішуючий елемент замінюється одиницею;

2. решта елементів вирішуючого стовпця залишається без змін:

3. решту елементів вирішуючого рядка змінюють знаки на протилежних;

4. елементи, які не належать вирішуючому рядку і вирішуючому стовпцю, визначається за правилом прямокутника:

b_ij=a_ij*a_ks-a_is*a_kj

де i, к-рядки; j, s - стовпці.