
- •2. Основна теорема теорії мн-нів.
- •3. Критерій розв’язуваності конгруенцій з одним невідомим першого степеня.
- •4. Основна теорема арифметики.
- •5. Знаходження оберненої матриці за допомогою визначників
- •6.Розв’язування с-ми лінійних рівнянь (слр) матричним способом. Формули Крамера.
- •7. Властивості множення матриць.
- •8. Критерій визначеності с-ми лінійних рівнянь (слр)
- •9. Критерій сумісності с-ми лінійних рівнянь .
- •1 0. Власт. Лз та лнз систем векторів.
- •11. Означення та вл-сті паралельних і розбіжних прямих на площині Лобачевського.
- •Дедекіндів переріз відрізка np
- •13. Аксіома Лобачевского. Основні факти геометрії.
- •14 Довжина дуги лінії на поверхні. Перша квадратична форма.
- •15. Дотична пряма і нормальна площина до гладкої просторової лінії. Виведення рівнянь.
- •16. Принцип двоїстості на проективній площині і в просторі. Теорема Дезарга.
- •1. Дано:
- •2. Дано:
- •17 Рухи. Властивості рухів. Класифікація рухів. Рухи
- •18.Рівняння площини і прямої в просторі.
- •1.Канонічне рівняння прямої.,
- •4. Параметричне р-ня прямої.
- •19.Змішаний добуток 3-х векторів. Геометр. Зміст змішаного добутку.
- •20.Векторний добуток 2-х векторів. Геометр. Зміст векторного добутку.
- •22. Похідна ф-ції комплексної змінної. Критерій існування. Умови Коші-Рімана.
- •23. Визначений інтеграл із змінною верхньою межею. Існування первісної неперервної ф-ції. Теорема Ньютона-Лейбніца.
- •24.Основні теореми диференціального числення (Ферма, Лагранжа, Коші, Роля)
- •26. Показникова і тригонометричні ф-ції в комплексній області.
- •27.Неперервні ф-ції та її властивості (теореми Больцано-Веєштраса I-II).
- •28. Означення границі ф-ції за Гейне і Коші.
- •30. Теорема Больцано – Вейєрштрасса (про підпослдовність).
26. Показникова і тригонометричні ф-ції в комплексній області.
Зрозуміло, що озн. sin i cos, яке ми мали для R змінної х, яке дається в елементарній матем. не може бути перенесене на аргумент, бо невідомо що розуміти під кутом (1+і) радіан. Щоб ввести ці ф-ції в обл. потрібно використати якісь ідеї. Цих ідей є декілька. Розгл. одну з них.
В R аналізі ми мали, що ф-ції sinx, cosx, ex розкладалися в наступні ряди Маклорена на всій R осі:
![]()
![]()
![]()
Зробимо формальну заміну х на число z:
![]() (1)
(1)
Для з’ясування
збіжності утворимо ряд з модулів:
![]() За
озн. Даламбера:
За
озн. Даламбера:
![]() .
.
Це озн., що ряд
абсолютно збіжний на всій
пл.,
а отже його сума є деяка ф-ція задана на
всій мн.
.
Оск. ф-ція, яка є сумою ряду (1) при
![]() ,
то логічно наз. цю ф-цію експонентою.
Позначається: expz.
Тому за озн. маємо:
,
то логічно наз. цю ф-цію експонентою.
Позначається: expz.
Тому за озн. маємо:
![]()
Аналогічно розв’язується проблема із sinz і cosz:
![]()
![]()
![]()
Розгл. Власт. одержаних в пл. ф-цій.
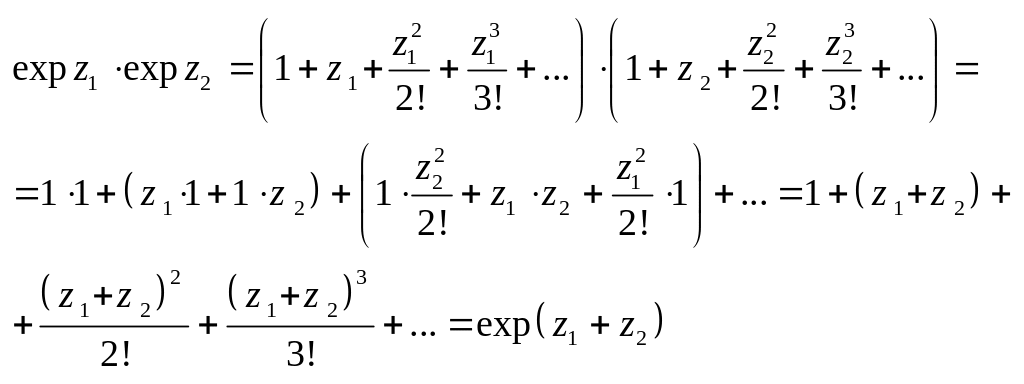
Отже,
![]() :
:
![]()
Отже:
![]()
![]()

Отже:
![]()
А остання рівність
озн., що поряд з алгебраїчною і
тригоно-метричною формою
числа
можна говорити і про експонен-ціальну
форму:
![]()
З’ясуємо (в зв’язку з останньою рівністю) чи 2kπi є періодом експоненціальної ф-ції.
![]()
А це озн., що експоненціальна ф-ція періодична з періодом 2kπi. Цей період є уявним числом і найменшим за модулем є число 2πi.
![]()
Додавши ці два ряди будемо мати:
![]()
![]() (2)
(2)
Віднявши останні два ряди будемо мати:
![]()
![]() (3)
(3)
![]() (4)
(4)
Формули (2), (3), (4) наз. формулами Ейлера.
Властивості sin i cos:
Із озн. цих ф-цій видно, що:sin(–z)=–sinz, cos(–z)=cosz
Враховуючи формули Ейлера одержимо, що ці ф-ції періодичні з тим же періодом, що і для R аргумента – 2π.
Перевіримо, чи справедливі тут формули додавання:

![]()
Аналогічно одержимо і інші формули додавання.
Покладемо: z2 = –z1 = z, cos 0 = cos2z+sin2z
1 = cos2z+sin2z
Займемось проблемою обмеженості cos і sin: виділимо дійсні та уявні частини кожної з цих ф-цій і оцінимо модуль кожної з них.
Скористаємось:
![]()
sin (iz) = i shz, cos (iz) = chz
Виділимо дійсну і уявну частину cos і sin.
![]()
 Отже,
ми одержали:
Отже,
ми одержали:
![]()
А оск. при y+ крайні частини останньої нерівності +, то остання нерівність дозволяє сказати: sin z в обл. є необмеженою ф-цією.Аналогічно для cos z.
27.Неперервні ф-ції та її властивості (теореми Больцано-Веєштраса I-II).
Озн.: Ф-ція F(x) наз.неперервною на мн. E , якщо вона неперервна в кожній т. цієї мн.
Т.1. Якщо y=f(x) і на кінцях цього відрізка приймає значення різних знаків, то хоча б одна точка с (a,b): f(c)=0 .
Дов. Позначимо через E мн. тих точок [a,b], в яких значення
ф-ції
>
0. E={x│x
[a,b],
f(x)>0}.
Оск. ф-ції
![]() (
в т.
неперервна справа ) то за т. про
консервативність
[а, а+
)
:
(
в т.
неперервна справа ) то за т. про
консервативність
[а, а+
)
:
![]()
f(x)>0.
Значить цей [а, а+
)
E.
Аналогічно з цієї т. одержимо мн. (
f(x)>0.
Значить цей [а, а+
)
E.
Аналогічно з цієї т. одержимо мн. (![]() ]:
]:
![]() (
],
f(x)>0,
а отже ні одна т. цього півокола
до
мн. Е.
(
],
f(x)>0,
а отже ні одна т. цього півокола
до
мн. Е.
Значить кожна із
точок (
]
включаючи і т. (![]() )
буде верхньою межею мн.Е .Отже
supE=с
при чому с
(a,b)
, бо ми довели, що а<c<b.
Звідси що
f(c)=0.
Прип.
що f(c)≠0.Тоді
за т. про консервативність
)
буде верхньою межею мн.Е .Отже
supE=с
при чому с
(a,b)
, бо ми довели, що а<c<b.
Звідси що
f(c)=0.
Прип.
що f(c)≠0.Тоді
за т. про консервативність
![]() [a,b]
:
[a,b]
:
![]() .Звідси
ні одна т. цього околу
Е.
Оск. с є верхньою межею мн. точок і ні
одне х
[a,b]:
x>c,
теж
Е.
Значить кожна т. з
.Звідси
ні одна т. цього околу
Е.
Оск. с є верхньою межею мн. точок і ні
одне х
[a,b]:
x>c,
теж
Е.
Значить кожна т. з![]() буде верхньою межею мн. Е, в тому числі
і точка
буде верхньою межею мн. Е, в тому числі
і точка
![]() .
Це неможливо, бо с – найменша з верхніх
меж. Протиріччя! Випадок f(c)>0
розглядається аналогічно.
.
Це неможливо, бо с – найменша з верхніх
меж. Протиріччя! Випадок f(c)>0
розглядається аналогічно.
Висновок: f(с)=0.
Т.2. Якщо
f(x)
і f(а)≠f(b),
то
![]() ,
що лежить між f(а)
і f(b)
,
що лежить між f(а)
і f(b)
![]()
Дов.
Нех. f(а)<f(b)
Розгл.![]() ,
,
![]()
![]()
![]() .
Тоді
.
Тоді
![]() задовольняє умови 1-ої т. Б-К
задовольняє умови 1-ої т. Б-К![]() ,
тобто
,
тобто
![]()
![]() .
.
Наслідок. Якщо функція неперервна на [a,b] то множиною її значень буде деякий відрізок або одно точкова множина.
