23.Дайте общую математическую формулировку задачи линейного программ-ния

Задачи линейного программирования относятся к категории оптимизационных. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования. Несмотря на различные области приложения, данные задачи имеют единую постановку: найти значения переменных x₁, …, x_n, доставляющие оптимум заданной линейной формы z=c₁x₁ + c₂x₂+… + c_nx_n при выполнении системы ограничений, представляющих собой также линейные формы.

Линейное прогр-ние – раздел т.оптим-ции, посвященный изучению и решению экстремальных задач, в к-ых линейная функция и ограничения, задающие допустимое множество, яв-ся линейными. Слово «программирование» объясняется тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно определяют программу (план) действий некоторого объекта, например, промышленного предприятия. Слово «линейное» отражает линейную зависимость между переменными.

Задача линейного программирования формулируется так:

Определить максимум линейной формы

F(x₁,…,x_n )=max(c₁x₁+…+c_nx_n) (8.3)

при условии, что точка (х₁, х₂,..., х_n) принадлежит некоторому множеству D, которое определяется системой линейных неравенств

(8.4)

Любое множество значений (х₁*, х₂*,..., х_n*), которое удовлетворяет системе неравенств (8.4) задачи линейного программирования, яв-ся допустимым решением данной задачи. Если при этом выполняется неравенство

c₁х₁^o+ c₂ х₂^o+..+ c_n х_n^o ≥ c₁х₁+ c₂ х₂+..+ c_n х_n

для всего множества значений x₁, х₂,..., х_n, то значение х₁^o..х_n^o яв-ся оптимальным решением задачи линейного программирования.

Задачу линейного программирования удобно представлять в векторной форме, тогда она будет выглядеть следующим образом: найти max F(x) = max (c^Tx) при условии АХ ≤Ро; Х≥0,

где с = (с₁,с₂,..., с_n) представляет собой n-мерный вектор, составленный из коэффициентов целевой функции, причем с^T-транспонированная вектор-строка; х = (х₁, х₂,..., х_п) - п-мерный вектор переменных решений;

- m-мерный вектор свободных членов ограничений;

Матрица А размером (m×n) - матрица, составленная из коэффициентов всех линейных ограничений:

П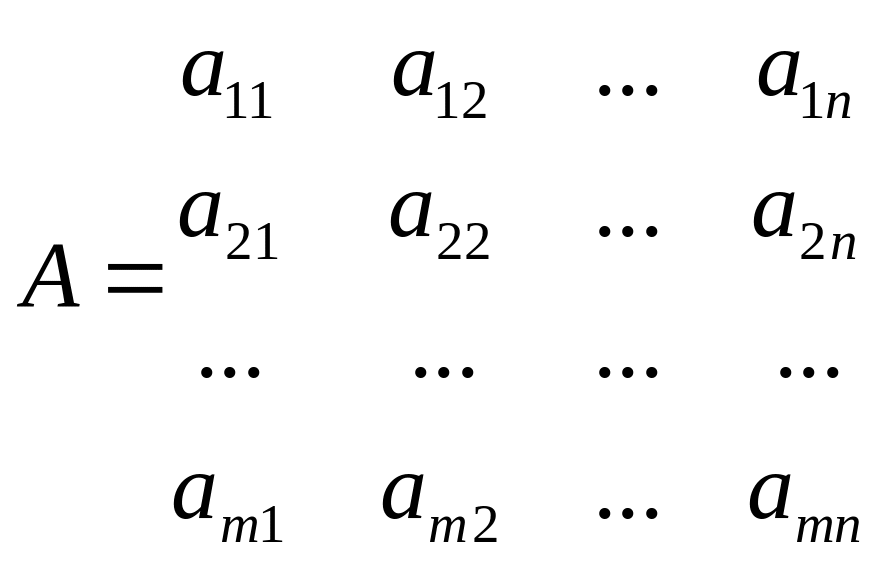 ростые ЗЛП допускают геометрическую интерпретацию, позволяющую непосредственно из графика получить решение и проиллюстрировать идею решения более сложных задач линейного программирования.

Каноническая задача линейного программирования заключается в минимизации (максимизации) линейной целевой функции

F(x) = c_lx₁+c₂x₂+... + c_nx_n при ограничениях

a₁₁х₁ +а₁₂х₂ +...+а_1пх_n=b₁

а₂₁х₁ +а₂₂х₂ +...+а_2пх_n=b_1…

…

а_m1х₁ +а_m2х₂ +...+а_mпх_n=b₁

x_t,x₂,...,x_n>0.

где с_[,с₂,...,с_п - коэффициенты целевой функции, a_tJ, i = \, 2,...,n,j = 1, 2,...,m -коэффициенты системы ограничений, а b₁,b_г,...,b_n - свободные члены, которые считаются неотрицательными.

Вектор X = (xi, х₂,..., xj, удовлетворяющий ограничениям задачи ЛП, называется допустимым решением или планом. Допустимый план X* =(xl,x'₂,...,x'_n), при котором целевая функция задачи ЛП принимает максимальное (минимальное) значение, на­зывается оптимальным планом.

И ными словами, каноническая задача линейного программирования (ЛП) состоит в нахождении среди всех решений выписанной выше системы линейных уравнений такого ее неотрицательного решения, на котором достигает своего минимального (максимального) значения линейная целевая функция z от и переменных.В задаче линейного программирования общего вида вместо некоторых (всех) равенств в ограничениях записаны нестрогие неравенства в ту или другую сторону; при этом усло­вие неотрицательности переменных может отсутствовать для части или же для всех переменных. Известно, что решение любой задачи линейного программирования может быть сведено к решению канонической задачи, представляемой в форме (1) или (4).Линейное программирование (ЛП) первоначально развивалось как направление, разрабатывающее новые подходы к решению задач минимизации выпуклых функций на выпуклом множестве (см. выпуклое программирование). Понятие целевой функции , удобное для приложений, сформировалось позднее.

Наиболее простым и распространенным методом решения канонической задачи линейного программирования до сих пор яв-ся симплекс-метод, предложенный в 40-е годы прошлого века Дж. Данцигом. Геометрически идею симплекс-метода в упрощенной форме можно выразить следующим образом. Допустимым множеством в задаче линейного программирования яв-ся некоторое многогранное множество и-мерного векторного пространства (в частном случае n = 2 - это выпуклый и не обязательно ограниченный многоугольник). Работа симплекс-метода начинается с некоторой начальной вершины (начального опорного плана) многогранного множества. Специальным образом выясняется, нет ли среди соседних вершин такой, в которой значение целевой функции лучше? Если такая вершина находится, то она и принимается за следующее приближение. После этого вновь исследуются соседние вершины для полученного приближения и т. д. до тех пор, пока не будет получена вершина, среди соседних вершин которой не существует вершины с лучшим значением целевой функции. Такая вершина яв-ся оптимальной. Она соответствует оптимальной точке (оптимальному решению) задачи линейного программирования.В настоящее время разработан широкий круг различных численных методов решения задач линейного профаммирования, каждый из которых учитывает ту или иную специфическую особенность имеющейся задачи линейного профаммирования.

. С применением линейного программирования решается широкий круг задач экономического характера: задачи о комплексном использовании сырья, рационального раскроя материалов, задачи загрузки оборудования, размещения заказов по однородным предприятиям, задачи о смесях, задачи текущего производственного планирования (статическая модель), задачи перспективного оптимального планирования, транспортная задача .