7

Министерство общего и профессионального образования

Российской федерации

Санкт-Петербургский государственный университет технологии и дизайна

А.Л. Сазонов

Теория вероятностей и математическая статистика

КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ

ПОСОБИЕ ДЛЯ СТУДЕНТОВ ВСЕХ СПЕЦИАЛЬНОСТЕЙ

Тетрадь № 2 Дискретные случайные величины

Санкт-Петербург

2000

Глава 2. Дискретные случайные величины

2.1. Закон распределения дискретной случайной величины

В главе 1 встречались примеры, в которых случайное событие состояло в том, что переменная величина принимала то или иное числовое значение, например, такие переменные, как число очков при бросании игральной кости, число попаданий в цель при двух выстрелах, число появлений герба при 10 подбрасываниях монеты и т. п. Такие переменные величины называются случайными.

Определение 1. Переменная величина называется случайной величиной (CB), если принятие ею любого допустимого значения является случайным событием.

Обычно случайные величины обозначаются заглавными буквами конца латинского алфавита X, Y, Z и т.д., а их значения соответствующими малыми буквами x, y, z, причем иногда с индексами. Так, например, если Х - число очков на игральной кости, то х₁ = 1, х₂ = 2, х₃ = 3, х₄ =4, х₅ = 5, х₆ = 6 - допустимые значения, а Х = х_i - случайное событие. В приведенных выше примерах множества допустимых значений случайных величин конечные последовательности. Можно рассмотреть и другие примеры. Например, случайная величина Y - число выстрелов до первого попадания в цель. Очевидно, что теоретически множество допустимых значений составляет бесконечную последовательность Y = {1, 2, ... , n, ...}. Или другой пример, случайная величина Z - скорость автомобиля, проезжающего данный участок пути. В этом примере множество допустимых значений составляет интервал (v_min; v_max). Последний пример качественно отличается от предыдущих, в которых множество допустимых значений - последовательности.

Определение 2. Случайная величина называется дискретной (ДСВ), если множество ее допустимых значений составляет конечную или бесконечную числовую последовательность.

Очевидно, Z - скорость автомобиля не является дискретной величиной.

В этой главе будут рассматриваться только дискретные случайные величины.

Каждому допустимому значению ДСВ (х_i) соответствует случайное событие Х = х_i, которое имеет определенную вероятность p_i , т.е. Р(Х = х_i) = p_i.

Определение 3. Соответствие между всеми допустимыми значениями ДСВ и вероятностями их появления называется законом распределения ДСВ .

Закон распределения ДСВ можно задать в виде таблицы. (См. табл.1).

Таблица 1

В этом случае говорят, что случайная величина Х подчиняется закону распределения (имеет закон распределения или распределена по закону), приведенному в табл.1.

Случайная величина в результате опыта обязательно принимает одно и только одно из всех ее допустимых значений, поэтому события Х = х_i, i=1,... , n

составляют полную группу попарно несовместимых событий, поэтому

(2.1.1)

Пример 1. Составить закон распределения числа очков при одном бросании игральной кости.

Очевидно, значения этой величины могут быть любыми целыми числами от 1 до 6, а все вероятности равны , поэтому закон распределения можно задать таблицей

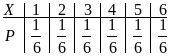
Замечание. Если множество допустимых значений дискретной случайной величины составляет бесконечную последовательность, то закон распределения - это бесконечная таблица. Ряд, составленный из вероятностей сходится и его сумма равна 1.

Пример 2. Найти закон распределения числа попаданий в цель при двух выстрелах, если вероятности попадания при первом выстреле 0,6 , а при втором - 0,8.

Обозначим А - попадание в цель при первом выстреле, В - при втором, Х - число попаданий при двух выстрелах. Тогда

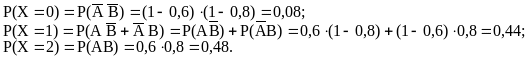
(Отметим, что одну из вероятностей можно найти на основании свойства закона распределения, т.е., скажем,

.

Таким образом закон распределения имеет вид

Определение 4. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какое значение приняла другая.

Например, при бросании двух игральных костей закон распределения числа очков на одной из них не зависит от того, сколько очков выпало на другой.

Пример 3. В урне имеется 10 шаров, на которых написаны дроби 1/2, 2/2, 2/2, 2/2, 1/3, 1/3, 1/3, 2/3, 2/3, 3/3. Из урны наудачу вынимают один шар. Случайная величина Х - числитель дроби, Y - знаменатель дроби на взятом шаре. Очевидно, что законы распределения этих величин имеют вид

Предположим, что вынут шар, знаменатель дроби на котором 2, т.е. Y = 2. Тогда закон распределения случайной величины Х уже будет иной

(Здесь использовано обозначение X/Y = 2 - случайная величина Х при условии, что случайная величина Y приняла значение 2. Последняя таблица называется условным законом распределения случайной величины Х при условии, что Y =2). Как мы видим, закон распределения стал уже иным, т.е. закон распределения Х зависит от того, какое значение приняла величина Y, следовательно, величины зависимы. Составьте самостоятельно условный закон распределения Х при условии, что Y = 3.

Табл.1 является полной характеристикой случайной величины. Однако, это не единственная его полная характеристика. Закон распределения может быть задан функцией.

Определение 5. Функцией распределения (интегральной функцией распределения или интегральным законом распределения) называется такая функция F(x), которая определена на всей числовой оси равенством

(2.1.2)

Из определения 5 следует, что каждое значение функции F(x₀) это вероятность того, что случайная величина Х принимает значение меньше, чем х₀.

Основные свойства функции распределения:

.

Если все допустимые значения случайной величины Х принадлежат промежутку , то справедливы также следующие свойства:

.

С помощью функции распределения можно найти вероятность того, что значение случайной величины попало в промежуток [, ): (2.1.3)

Например, для случайной величины Х из примера 2

функция распределения - это ступенчатая функция

Объясните на основании определения 5 самостоятельно, почему функция имеет такой вид и постройте ее график. Найдите F(x) для X = c - const.