
Задание n 11 Тема: Группы и подгруппы
Операция «+» – сложения образует группу на множестве …
|
|
|
целых четных чисел |
|
|
|
натуральных чисел |
|
|
|
целых нечетных чисел |
|
|
|
действительных чисел без нуля |
Решение: Множество целых четных чисел с введенной операцией сложения образует группу. Множество натуральных чисел не группа, так как, например, не имеет противоположного элемента. Множество целых нечетных не имеет нулевого элемента, как и множество действительных чисел без нуля.
Задание n 12 Тема: Линейные отображения
Линейным отображением пространства трехмерных векторов на пространство двумерных векторов является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Линейным
называется отображение
удовлетворяющее
условиям:
![]() ,
,
![]() .
Проверим
на линейность отображение
:
.
Проверим
на линейность отображение
:
![]() ,
,
![]() ,
Следовательно
,
Следовательно
![]() –
первое условие не выполнено, а значит
не
является линейным отображением.
Для
отображения
проверим
выполнение второго условия:
–
первое условие не выполнено, а значит
не
является линейным отображением.
Для
отображения
проверим
выполнение второго условия:
![]() Условие
не выполняется, значит
не
линейное отображение.
Проверим
выполнение второго условия для отображения
:
Условие
не выполняется, значит
не
линейное отображение.
Проверим
выполнение второго условия для отображения
:
![]() Следовательно,
данное отображение не является
линейным.
Проверим выполнение условий
линейности для отображения
:
Следовательно,
данное отображение не является
линейным.
Проверим выполнение условий
линейности для отображения
:
![]() ,
,
![]() ,
Следовательно
,
Следовательно
![]() –
первое условие выполнено.
–
первое условие выполнено.
![]() –
второе условие выполнено. Поэтому
является
линейным отображением.
–
второе условие выполнено. Поэтому
является
линейным отображением.
ЗАДАНИЕ N 13 Тема: Прямая линия в пространстве
Прямая
![]() параллельна
плоскости
параллельна
плоскости
![]() ,
если параметр
,
если параметр
![]() равен
…
равен
…
|
|
|
– 11 |
|
|
|
– 7 |
|
|
|
7 |
|
|
|
11 |
ЗАДАНИЕ N 14 Тема: Кривые второго порядка
Уравнением
кривой второго порядка
![]() на
плоскости определяется …
на
плоскости определяется …
|
|
|
эллипс |
|
|
|
гипербола |
|
|
|
парабола |
|
|
|
пара пересекающихся прямых |
Решение:
Выделим
в уравнении
полный
квадрат по переменной
:
![]() ,
или
,
или
![]() .
Разделив обе части этого уравнения на
10, получим уравнение вида:
.
Разделив обе части этого уравнения на
10, получим уравнение вида:
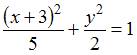 ,
которое на плоскости определяет эллипс.
,
которое на плоскости определяет эллипс.
ЗАДАНИЕ N 15 Тема: Прямоугольные координаты на плоскости
Даны точки и . Тогда координаты точки , симметричной точке относительно точки , равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 16 Тема: Плоскость в пространстве
Плоскость,
проходящая через точки
![]() и
и
![]() параллельно
оси
параллельно
оси
![]() ,
задается уравнением …
,
задается уравнением …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Общее
уравнение плоскости, параллельной оси
,
имеет вид:
![]() .
Точки
и
лежат
в искомой плоскости, следовательно, их
координаты удовлетворяют уравнению
:
.
Точки
и
лежат
в искомой плоскости, следовательно, их
координаты удовлетворяют уравнению
:
 ,
отсюда
,
отсюда
![]() ,
,
![]() .
Подставим найденные значения в уравнение
плоскости:
.
Подставим найденные значения в уравнение
плоскости:
![]() или
или
![]() ,
то есть
.
,
то есть
.
ЗАДАНИЕ N 17 Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – десять, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
ЗАДАНИЕ N 18 Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
вероятность
Тогда
вероятность
![]() равна
…
равна
…
|
|
|
0,8 |
|
|
|
0,3 |
|
|
|
0,7 |
|
|
|
0,4 |
ЗАДАНИЕ N 19 Тема: Полная вероятность. Формулы Байеса
Банк выдает 40% всех кредитов юридическим лицам, а 60% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,1; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило физическое лицо, равна …
|
|
|
|
|
|
|
|
|
|
|
0,07 |
|
|
|
0,05 |
Решение:
Предварительно
вычислим вероятность события A
(выданный кредит не будет погашен в
срок) по формуле полной вероятности:
.
Здесь
–
вероятность того, что кредит был выдан
юридическому лицу;
–
вероятность того, что кредит был выдан
физическому лицу;
–
условная вероятность того, что кредит
не будет погашен в срок, если он был
выдан юридическому лицу;
–
условная вероятность того, что кредит
не будет погашен в срок, если он был
выдан физическому лицу. Тогда
![]() .
Теперь
вычислим условную вероятность того,
что этот кредит не погасило физическое
лицо, по формуле Байеса:
.
Теперь
вычислим условную вероятность того,
что этот кредит не погасило физическое
лицо, по формуле Байеса:
 .
.
ЗАДАНИЕ N 20 Тема: Числовые характеристики случайных величин
Математическое
ожидание дискретной случайной величины
,
заданной законом распределения
вероятностей:
 равно
4,4. Тогда значение вероятности
равно
4,4. Тогда значение вероятности
![]() равно
…
равно
…
|
|
|
0,7 |
|
|
|
0,3 |
|
|
|
0,6 |
|
|
|
0,4 |
Решение:
Математическое
ожидание дискретной случайной величины
вычисляется по формуле
 .
Тогда
.
Тогда
![]() .
А с учетом условия
.
А с учетом условия
![]() получаем
систему уравнений:
получаем
систему уравнений:
 решение
которой имеет вид:
решение
которой имеет вид:
![]() ,
,
![]() .
.
ЗАДАНИЕ N 21 Тема: Интервальные оценки параметров распределения
Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 22 Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема , гистограмма частот которой имеет вид: Тогда значение a равно …
|
|
|
38 |
|
|
|
39 |
|
|
|
76 |
|
|
|
37 |
ЗАДАНИЕ N 23 Тема: Проверка статистических гипотез
Для
проверки нулевой гипотезы
![]() при
заданном уровне значимости
при
заданном уровне значимости
![]() выдвинута
конкурирующая гипотеза
выдвинута
конкурирующая гипотеза
![]() .
Тогда область принятия гипотезы может
иметь вид …
.
Тогда область принятия гипотезы может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 24 Тема: Элементы корреляционного анализа
При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции и выборочные средние квадратические отклонения . Тогда выборочный коэффициент регрессии на равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выборочный
коэффициент регрессии
на
вычисляется
по формуле
 .
Тогда
.
Тогда
 .
.
ЗАДАНИЕ N 25 Тема: Отображение множеств
Отображение
![]() действует
по правилу:
действует
по правилу:
 Тогда
Тогда
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как
![]() при
при
![]() и
и
![]() при
при
![]() ,
то
,
то
![]() .
.
ЗАДАНИЕ N 26 Тема: Элементы теории множеств
Даны
три множества:
![]() ,
,
![]() и
и
![]() .
Тогда число элементов множества
.
Тогда число элементов множества
![]() равно
…
равно
…
|
3 | |
Решение:
Выполним
операцию в скобках, то есть определим
множество
![]() .
Теперь выполним вычитание, в результате
которого получится множество чисел,
принадлежащих
.
Теперь выполним вычитание, в результате
которого получится множество чисел,
принадлежащих
![]() ,
но без чисел множества
:
,
но без чисел множества
:
![]() .
Таким образом, множество
содержит
три элемента.
.
Таким образом, множество
содержит
три элемента.
ЗАДАНИЕ N 27 Тема: Метрические пространства
Расстояние между точками и в метрике , где и , равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
ЗАДАНИЕ N 28 Тема: Мера плоского множества
Мера
плоского множества
![]() ,
где А=
,
где А=![]() и
и
![]() равна
…
равна
…
|
|
|
|
|
|
|
4 |
|
|
|
0 |
|
|
|
1 |
Решение:
Мера
плоского множества
равна
площади соответствующей фигуры, то есть
квадрата со стороной 2. Мера плоского
множества
![]() равна
площади соответствующей фигуры, то есть
круга с радиусом 1. Так как круг целиком
лежит внутри квадрата, то искомая мера
равна
.
равна
площади соответствующей фигуры, то есть
круга с радиусом 1. Так как круг целиком
лежит внутри квадрата, то искомая мера
равна
.
ЗАДАНИЕ N 29 Тема: Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 30 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Дана
функция
![]() .
Тогда меньший действительный корень
производной этой функции принадлежит
промежутку …
.
Тогда меньший действительный корень
производной этой функции принадлежит
промежутку …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Эта
функция представляет собой полином
6-го порядка и дифференцируема на всей
числовой оси. Согласно теореме Ролля
между двумя корнями (нулями) этой функции
находится по крайней мере один корень
ее производной. Поскольку
![]() представляет
собой полином (5-го порядка), то между
двумя корнями функции
представляет
собой полином (5-го порядка), то между
двумя корнями функции
![]() находится
ровно один корень ее производной
.
Найдем
корни функции
:
находится
ровно один корень ее производной
.
Найдем
корни функции
:
![]() .
Тогда меньший действительный корень
функции
принадлежит
интервалу
.
.
Тогда меньший действительный корень
функции
принадлежит
интервалу
.
ЗАДАНИЕ N 31 Тема: Непрерывность функции, точки разрыва
Для функции точка является точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Решение:
Вычислим
односторонние пределы функции
в
точке
:
 ,
,
 .
Так
как один из односторонних пределов в
точке
,
а именно
.
Так
как один из односторонних пределов в
точке
,
а именно
![]() ,
то точка
является
точкой разрыва второго рода.
,
то точка
является
точкой разрыва второго рода.
ЗАДАНИЕ N 32 Тема: Дифференциальное исчисление ФНП
Частная
производная второго порядка
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При
вычислении частной производной функции
![]() по
одной из переменных другую переменную
рассматриваем как постоянную величину.
Тогда
по
одной из переменных другую переменную
рассматриваем как постоянную величину.
Тогда
 .
.
ЗАДАНИЕ N 33 Тема: Элементы комбинаторики
В урне находятся 10 белых, 15 красных, 20 голубых шаров. Все шары пронумерованы. Сколькими различными способами можно взять из урны три шара разных цветов?
|
3000 | |
Решение:
Возьмем
один белый шар. Это действие можно
выполнить 10 способами (по числу различных
белых шаров в урне). К выбранному белому
шару присоединим красный шар, который
можно взять 15 различными способами (по
числу различных красных шаров в урне).
К выбранной присоединим голубой шар,
который можно взять 20 способами (по
числу различных голубых шаров в урне).
Таким образом, можно образовать различные
тройки разноцветных шаров. Число
различных способов выбора троек
разноцветных шаров совпадает с числом
различных трех действий и по правилу
умножения равно:
![]()
ЗАДАНИЕ N 34 Тема: Операции над высказываниями
Для
функции
![]() ,
заданной таблицей,
,
заданной таблицей,
 СДНФ
имеет вид …
СДНФ
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
СДНФ
будет выглядеть следующим образом:
![]()
ЗАДАНИЕ N 35 Тема: Неориентированные графы
Для графа, изображенного на рисунке, последовательность является …
|
|
|
маршрутом |
|
|
|
цепью |
|
|
|
циклом |
|
|
|
деревом |
ЗАДАНИЕ N 36 Тема: Декартово произведение множеств
Даны
множества
![]() ,
,
![]() и
и
![]() .
Тогда число элементов декартова
произведения множеств
.
Тогда число элементов декартова
произведения множеств
![]() равно…
равно…
|
|
|
8 |
|
|
|
6 |
|
|
|
12 |
|
|
|
4 |
Решение:
Декартово
произведение множеств – это множество,
состоящее из упорядоченных пар элементов,
первым элементом которых являются
элементы первого множества, вторым –
элементы второго, то есть
 Данное
множество содержит восемь элементов.
Данное
множество содержит восемь элементов.
ЗАДАНИЕ N 37 Тема: Дифференциальная геометрия поверхностей
Первая
квадратичная форма поверхности
 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Запишем
поверхность в виде вектор-функции
![]() и
вычислим частные производные:
,
и
вычислим частные производные:
,
![]() .
Коэффициенты
первой квадратичной формы
.
Коэффициенты
первой квадратичной формы
![]() определим
по формулам:
определим
по формулам:
![]() ;
;
![]() ;
;
![]() .
Тогда
.
Тогда
![]() ;
;
![]() ;
;
![]() .
Таким
образом,
.
.
Таким
образом,
.
ЗАДАНИЕ N 38 Тема: Дифференциальная геометрия кривых
Длина дуги кривой при , равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,14 |
ЗАДАНИЕ N 39 Тема: Асимптоты кривой
Асимптоты
кривой
![]() имеют
вид …
имеют
вид …
Математика i-exam вариант 5
ЗАДАНИЕ N 1 Тема: Поле направлений и изоклины
Поле направлений дифференциального уравнения определяется неравенством …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Так как поле направлений дифференциального уравнения задано в области определения функции двух переменных , то для нахождения области задания поля направлений следует решить неравенство . Тогда .
ЗАДАНИЕ N 2 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Решение
задачи Коши

![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Решим
систему дифференциальных уравнений
методом исключения.
Из второго
уравнения находим
![]() ,
откуда
,
откуда![]() ;
после подстановки в первое уравнение
системы получим линейное неоднородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами
;
после подстановки в первое уравнение
системы получим линейное неоднородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами
![]() .
Характеристическое уравнение
.
Характеристическое уравнение
![]() имеет
два действительных корня:
имеет
два действительных корня:
![]() .
Таким корням соответствует общее решение
однородного дифференциального уравнения
.
Таким корням соответствует общее решение
однородного дифференциального уравнения
![]() .
Поскольку
правая часть исходного уравнения
.
Поскольку
правая часть исходного уравнения
![]() ,
то имеем уравнение со специальной правой
частью.
Так как
,
то имеем уравнение со специальной правой
частью.
Так как
![]() не
является корнем характеристического
уравнения, то частное решение
не
является корнем характеристического
уравнения, то частное решение
![]() неоднородного
уравнения будем искать в виде
неоднородного
уравнения будем искать в виде
![]() .
Найдя
производные первого и второго порядков
и подставив в уравнение
.
Найдя
производные первого и второго порядков
и подставив в уравнение
![]() ,
получим
,
получим
![]() .
Тогда
общее решение этого уравнения имеет
вид
.
Тогда
общее решение этого уравнения имеет
вид
![]() .
Дифференцируя полученное решение,
находим
.
Дифференцируя полученное решение,
находим
![]() и
и
 Значит,
общее решение системы уравнений имеет
вид
Значит,
общее решение системы уравнений имеет
вид
![]() .
Найдем
значения произвольных постоянных
.
Найдем
значения произвольных постоянных
![]() и
и
![]() ,
соответствующих исходной задаче Коши,
подставляя начальные условия в общее
решение. Получим систему уравнений
,
соответствующих исходной задаче Коши,
подставляя начальные условия в общее
решение. Получим систему уравнений
 или
или
 Решая
эту систему, находим значения постоянных
величин
Решая
эту систему, находим значения постоянных
величин
![]() .
Поэтому
решение задачи Коши имеет вид
.
Поэтому
решение задачи Коши имеет вид
![]() .
.
ЗАДАНИЕ N 3 Тема: Дифференциальные уравнения с разделяющимися переменными
Если угловой коэффициент касательной к кривой в любой ее точке вдвое больше углового коэффициента радиуса-вектора точки касания, то уравнение этой кривой будет иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 4 Тема: Задача Коши для дифференциального уравнения первого порядка
Частное
решение дифференциального уравнения
![]() ,
удовлетворяющее условию
,
удовлетворяющее условию
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Введем
замену
![]() ;
;
![]() .
Тогда уравнение
примет
вид
.
Тогда уравнение
примет
вид
![]() ,
или
,
или
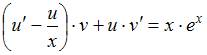 .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда
![]() .
Подставим найденное значение
.
Подставим найденное значение
![]() в
уравнение
.
Получим:
в
уравнение
.
Получим:
![]() ,
то есть
,
то есть
![]() и
и
![]() .
Общее
решение примет вид
.
Общее
решение примет вид
![]() .
Подставив начальное условие, получим
.
Подставив начальное условие, получим
![]() .
Откуда
.
Откуда
![]() и
частное решение будет иметь вид
.
и
частное решение будет иметь вид
.
ЗАДАНИЕ N 5 Тема: Элементы теории множеств
Даны
два множества:
![]() и
и
![]() .
Тогда количество целых значений
,
принадлежащих разности множеств
\
,
равно …
.
Тогда количество целых значений
,
принадлежащих разности множеств
\
,
равно …
|
4 |
ЗАДАНИЕ N 6 Тема: Отображение множеств
Пусть
задано отображение
![]() .
Тогда
.
Тогда
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 7 Тема: Метрические пространства
Функция
![]() ,
где
,
где
![]() –
действительные числа, …
–
действительные числа, …
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме треугольника |
ЗАДАНИЕ N 8 Тема: Мера плоского множества
Мера плоского множества равна …
|
|
|
4 |
|
|
|
1 |
|
|
|
2 |
|
|
|
0 |
Решение: Мера плоского множества равна площади соответствующей фигуры, то есть квадрата со стороной 2. Следовательно, мера этого множества равна 4.
ЗАДАНИЕ N 9 Тема: Плоскость в пространстве
Уравнение
плоскости, проходящей через точки
![]() ,
,
![]() и
и
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 10 Тема: Прямая линия в пространстве
Точка
пересечения прямой
![]() и
плоскости
и
плоскости
![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Запишем
уравнение прямой в параметрическом
виде:
 ,
то есть
,
то есть
 .
Подставим
полученные уравнения в уравнение
плоскости
.
Тогда
.
Подставим
полученные уравнения в уравнение
плоскости
.
Тогда
![]() ,
или
,
или
![]() .
Подставляя значение параметра
в
систему параметрических уравнений
.
Подставляя значение параметра
в
систему параметрических уравнений
 ,
найдем координаты точки пересечения
прямой и плоскости
.
,
найдем координаты точки пересечения
прямой и плоскости
.
ЗАДАНИЕ N 11 Тема: Прямоугольные координаты на плоскости
В
треугольнике с вершинами
![]() ,
,
![]() и
и
![]() проведена
медиана
проведена
медиана
![]() ,
длина которой равна …
,
длина которой равна …
|
|
|
4 |
|
|
|
|
|
|
|
16 |
|
|
|
|
Решение:
Точка
является
серединой отрезка
![]() .
Координаты середины отрезка определяются
по формулам
.
Координаты середины отрезка определяются
по формулам
![]() ,
,
![]() .
Подставляя в эти формулы координаты
точек
и
,
получим координаты точки
:
.
Подставляя в эти формулы координаты
точек
и
,
получим координаты точки
:
![]() ,
,
![]() .
Расстояние между точками
и
можно
найти по формуле
.
Расстояние между точками
и
можно
найти по формуле
![]() .
То
есть
.
То
есть
![]() .
.
ЗАДАНИЕ N 12 Тема: Кривые второго порядка
Асимптоты
гиперболы
![]() задаются
уравнениями …
задаются
уравнениями …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Асимптоты
гиперболы
 задаются
уравнениями вида
задаются
уравнениями вида
![]() .
Разделив обе части уравнения
на
36, получим каноническое уравнение
гиперболы:
.
Разделив обе части уравнения
на
36, получим каноническое уравнение
гиперболы:
 .
То есть
.
То есть
![]() и
и
![]() .
Тогда уравнения асимптот примут вид
.
.
Тогда уравнения асимптот примут вид
.
ЗАДАНИЕ N 13 Тема: Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема
![]() ,
полигон относительных частот которой
имеет вид:
,
полигон относительных частот которой
имеет вид:
 Тогда
число вариант
Тогда
число вариант
![]() в
выборке равно …
в
выборке равно …
|
|
|
37 |
|
|
|
63 |
|
|
|
100 |
|
|
|
36 |
ЗАДАНИЕ N 14 Тема: Проверка статистических гипотез
Основная
гипотеза имеет вид
![]() .
Тогда конкурирующей может являться
гипотеза …
.
Тогда конкурирующей может являться
гипотеза …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 15 Тема: Интервальные оценки параметров распределения
Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала , где точечная оценка математического ожидания , а точность оценки . В случае уменьшения объема выборки точность оценки ухудшается, то есть значение будет больше 2,13.
ЗАДАНИЕ N 16 Тема: Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии
на
имеет
вид
![]() .
Тогда выборочное среднее признака
равно
…
.
Тогда выборочное среднее признака
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выборочное
уравнение прямой линии регрессии
на
имеет
вид
![]() .
Тогда выборочное среднее признака
равно
.
Тогда выборочное среднее признака
равно
![]() .
.
ЗАДАНИЕ N 17 Тема: Дифференцирование функции комплексного переменного
Если , то равно …
|
|
|
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 18 Тема: Области на комплексной плоскости
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 19 Тема: Операции над комплексными числами
Если и – корни квадратного уравнения , то равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 20 Тема: Особые точки функции комплексного переменного
Для функции точка является …
|
|
|
полюсом второго порядка |
|
|
|
полюсом третьего порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
Решение:
Порядок
полюса функции вида
равен
порядку нуля
.
Так
как
 ,
то точка
будет
полюсом второго порядка.
,
то точка
будет
полюсом второго порядка.
ЗАДАНИЕ N 21 Тема: Асимптоты кривой
Асимптоты кривой имеют вид …
|
|
|
и |
|
|
|
и |
|
|
|
и |
|
|
|
и |
Решение:
Кривая
описывается соотношением
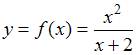 ,
то есть функция представлена в явном
виде.
В точке
функция
имеет разрыв второго рода, поэтому
уравнение вертикальной асимптоты имеет
вид:
.
Наклонные
или горизонтальные асимптоты определяются
уравнением
(для
горизонтальных асимптот
).
1.
Находим асимптоту
при
(правую
асимптоту):
,
то есть функция представлена в явном
виде.
В точке
функция
имеет разрыв второго рода, поэтому
уравнение вертикальной асимптоты имеет
вид:
.
Наклонные
или горизонтальные асимптоты определяются
уравнением
(для
горизонтальных асимптот
).
1.
Находим асимптоту
при
(правую
асимптоту):
 ,
,
 .
Следовательно,
уравнение правой асимптоты имеет
вид:
.
2.
Аналогично находим асимптоту
при
(левую
асимптоту):
.
Следовательно,
уравнение правой асимптоты имеет
вид:
.
2.
Аналогично находим асимптоту
при
(левую
асимптоту):
 ,
,
 .
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптотой и имеет
вид:
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
.
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптотой и имеет
вид:
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
Математика i-exam вариант 6
ЗАДАНИЕ N 1 Тема: Проверка статистических гипотез
Соотношением вида можно определить …
|
|
|
правостороннюю критическую область |
|
|
|
левостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
ЗАДАНИЕ N 2 Тема: Элементы корреляционного анализа
При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции и выборочные средние квадратические отклонения . Тогда выборочный коэффициент регрессии на равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 3 Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема , гистограмма частот которой имеет вид: Тогда значение a равно …
|
|
|
38 |
|
|
|
39 |
|
|
|
76 |
|
|
|
37 |
ЗАДАНИЕ N 4 Тема: Интервальные оценки параметров распределения
Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала , где точечная оценка математического ожидания , а точность оценки . В случае уменьшения объема выборки точность оценки ухудшается, то есть значение будет больше 2,13.
ЗАДАНИЕ N 5 Тема: Операции над высказываниями
Из трех логических выражений: эквивалентными являются …
|
|
|
и |
|
|
|
и |
|
|
|
и |
|
|
|
все функции |
ЗАДАНИЕ N 6 Тема: Элементы комбинаторики
Из города в город ведут 5 дорог, из в – 3 дороги, имеются также 2 дороги из в , минуя . Из в можно попасть ____ способом(-ами).
|
17 | |
Решение: Из города в город можно попасть способами, из в – с помощью способов. Тогда из в через можно попасть способами (по правилу произведения); а из в , минуя , можно попасть способами. Поэтому по правилу суммы общее число способов, которыми можно попасть из города в город , равно: .
ЗАДАНИЕ N 7 Тема: Декартово произведение множеств
Пусть заданы два множества: , . Тогда геометрическая интерпретация множества имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 8 Тема: Неориентированные графы
Эйлеровым является граф …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дифференциальная геометрия кривых
Траектория движущейся точки задается уравнением Тогда значение касательного ускорения в момент равно …
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение: Касательное ускорение на параметрически заданной кривой вычисляется как . Вычислим производные первого и второго порядка. Найдем , при любых значениях .
ЗАДАНИЕ N 10 Тема: Дифференциальная геометрия поверхностей
Точка с координатами на поверхности является …
|
|
|
гиперболической точкой |
|
|
|
параболической точкой |
|
|
|
эллиптической точкой |
|
|
|
точкой уплощения |
Решение: Тип точки на поверхности определяется по виду соприкасающегося параболоида в этой точке к поверхности. Построим соприкасающийся параболоид: . Вычислим частные производные второго порядка: ; ; . В точке ; ; . Тогда соприкасающийся параболоид является гиперболическим параболоидом, а сама точка относится к гиперболическому типу.




