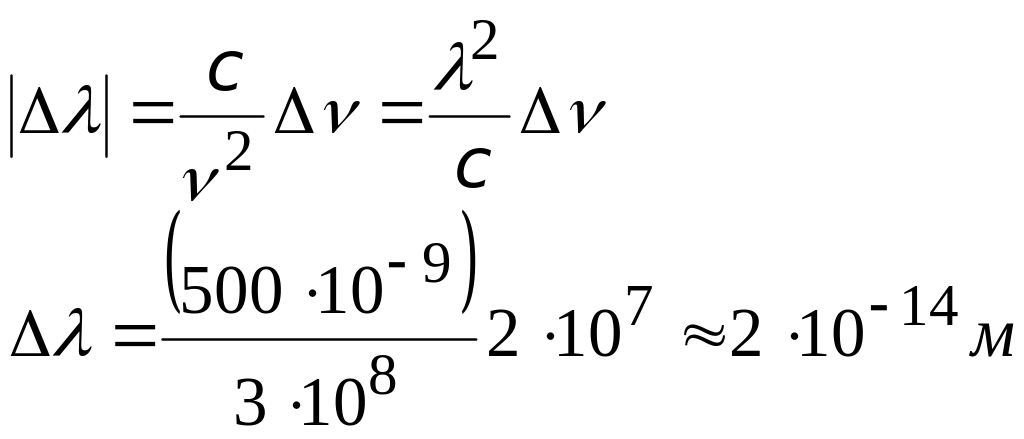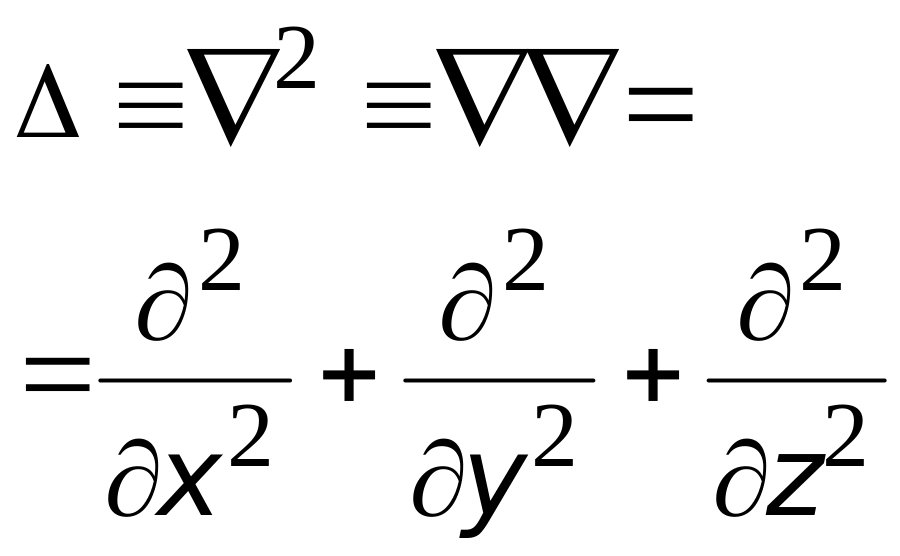- •Квантовая физика.
- •Распределение энергии в спектре ачт.
- •Гипотеза и формула Планка.
- •2) Для элементарных процессов взаимодействия частиц применимы законы сохранения импульса и энергии.
- •Ядерная модель атома.
- •Постулаты Бора:
- •Атом водорода и водородоподобные атомы (впа) по теории Бора.
- •Корпускулярно-волновой дуализм материи. Гипотеза и формула де Бройля.
- •Принцип неопределенности Гейзенберга.
- •1). Входит ли электрон в состав атомного ядра?
- •Уравнение Шрёдингера.
- •Гармонический осциллятор.
- •Частица в одномерной потенциальной яме (ящике)
- •Электрон в атоме водорода в основном состоянии.
- •Описывается с помощью 4-х квантовых чисел: n, l, m, ms.
- •Принцип Паули. Периодическая система элементов.
- •Элементы квантовой статистики и физики твердого тела.
- •Сверхтекучесть.
- •Сверхпроводимость.
- •Температурная зависимость сопротивления различных веществ.
- •Собственные полупроводники.
- •Контакт р - и n - полупроводников.
- •105 - 104 См, для металлов порядка 108 см.
1). Входит ли электрон в состав атомного ядра?
х = 1014 м |
Размер ядра по порядку величины |
|
Предположим, что электрон находится в ядре. Найдем неопределенность в его импульсе и примем ее равной самому импульсуxiv |
|
кинетическая энергия релятивистского электрона в ядре (считаем, что он движется как квант со скоростью с) |
Из опытов по радиоактивному бета-распаду известно, что энергии вылетающих из ядра электронов значительно меньше. Следовательно, в ядре «готовых» электронов нет; электрон образуется в ядре при превращении нейтрона в протон. |
|
2). Оценим с помощью соотношения неопределенностей энергию связи электрона в атоме водорода.
х =0,5 1010 м |
размер атома Н |
|
импульс электрона, вычисленный с помощью соотношения неопределенности |
|
Энергия нерелятивистского электрона (1 эВ=1,61019 Дж). По порядку величины совпадает с энергией, вычисленной по теории Бора |
3). Найдем предел точности, с которой можно определить частоту и длину волны излучаемого света
|
время возбужденного атома, спустя это время электрон возвращается на нижележащую орбиту, и атом испускает квант света с энергией Е |
|
предел точности определения частоты излучения, найденный с помощью соотношения неопределенности |
|
предел точности измерения длины световой волны для зеленого света =(500,0000000 0,0000002) нм с = 3108 м/с – скорость света в вакууме |
Уравнение Шрёдингера.
Открытие двойственной природы частиц привело к пониманию о невозможности описывать поведение микрочастиц с помощью классических представлений и законов. Стало ясно, что нельзя говорить о траектории частицы, т.е. о точном ее местоположении в любой момент времени. Появилась новая наука – квантовая механика. Вместо слова траектория частицы было введено понятие о вероятности нахождения частицы в том или ином месте пространства. Для описания поведения микрочастиц Шрёдингер (1926 г) предложил дифференциальное уравнение:
|
нестационарное уравнение Шрёдингера; решение уравнения позволяет найти вероятность нахождения частицы в том или ином мете пространства |
|
|
мнимая единица |
|
m |
масса рассматриваемой частицы |
|
U(x,y,z,t) |
потенциальная энергия частицы, зависящая в общем случае от координат и времени |
|
|
оператор Лапласа
(или лапласиан) краткое обозначение
математической операции дифференцирования
в частных производных;
|
|
(x,y,z,t) |
пси-функция или волновая функция, физического смысла не имеет, но квадрат ее модуля 2 – это вероятность нахождения частицы в данном месте пространства (подробнее см. дальше – стационарное уравнение Шрёдингера) |
|
Математически уравнение Шрёдингера имеет бесконечное число решений, что физически неприемлемо, поэтому на пси-функцию накладываются дополнительные условия:
1).Пси-функция должна быть:
а) конечной – вероятность не может быть больше 1,
б) непрерывной – вероятность не может внезапно оборваться,
в) однозначной – не может быть две вероятности в одной точке,
2) Производные пси-функции должны быть непрерывны,
3) Пси-функция должна подчиняться условию нормировки:
|
условие нормировки; смысл его в том, что вероятность обнаружить частицу во всем мыслимом пространстве равна 1. |
В тех случаях, когда потенциальная энергия зависит только от координат и не зависит от времени, т.е U = U (x,y,z), пси-функцию можно представить как произведение двух функций: (x,y,z,t) = ( x,y,z) (t). ( - большая буква пси,
- малая буква пси, обе функции называются пси- или волновыми функциями.) Подставим в уравнение () и, разделим на ().. Получим:
|
Левая часть уравнения зависит только от t, правая – только от координат, следовательно, каждая из них должна быть равна некоторой постоянной, которую мы обозначим Е. |
|||
|
|
|
(t) называется временнОй частью пси-функции, со временем она затухает |
|
Если приравнять константе Е правую часть уравнения, получим:
|
стационарное уравнение Шрёдингера Е – полная энергия частицы, U – потенциальная энергия |
При решении уравнения Шредингера мы
задаем |
находим |
U – потенциальную энергию частицы m – массу частицы |
- пси-функцию (собственные функции) Е – полную энергию частицы (собственные значения) |
Решение уравнения с учетом дополнительных условий, накладываемых на пси-функцию, приводит не к любым величинам энергии Е, а к дискретным:
Е1, Е2,…, Еn . В теории Бора электрон мог находиться тоже только в дискретных энергетических состояниях, но при этом была введена искусственно гипотеза о квантовании момента импульса электрона. Уравнение Шрёдингера приводит к квантованию энергии естественно, как математическое решение.
При решении
оказывается, что данному энергетическому
состоянию частицы могут соответствовать
одна или несколько (к)
пси-функций. Иначе говоря, при данной
энергии Еn
частица
может вести себя по-разному. Тогда
говорят, что уровень Еn
к-кратно
вырожден и обозначают пси-функцию как
![]() Если на систему воздействовать внешним,
например магнитным полем, то вырождение
снимается, уровень расщепляется на
несколько уровней. Практически это
обнаруживается в спектрах, вместо одной
линии появляются несколько. Например,
в спектре атома водорода на приборе с
большим разрешением можно обнаружить,
что почти все линии спектра являются
дублетами.
Если на систему воздействовать внешним,
например магнитным полем, то вырождение
снимается, уровень расщепляется на
несколько уровней. Практически это
обнаруживается в спектрах, вместо одной
линии появляются несколько. Например,
в спектре атома водорода на приборе с
большим разрешением можно обнаружить,
что почти все линии спектра являются
дублетами.
Рассмотрим подробнее пси-функцию.
- пси-функция |
физического смысла не имеет |
|
для 3-х-мерного случая |
плотность вероятности (квадрат модуля пси-функции) – по смыслу – это вероятность того, что частица находится в единичном объеме в данном месте пространства Р – вероятность. |
|
для одномерного случая |
…. вероятность того, что частица находится на единичном отрезке… |
|
|
вероятность того, что частица находится в элементарном объеме dV |
|
|
вероятность того, что частица находится в конечном объеме V |
|
|
вероятность того, что частица находится во всем пространстве |
|
Уравнение
Шрёдингера ()
решается точно только для упрощенных,
нереальных случаев, например, электрон
в одномерной потенциальной яме. Из
реальных объектов уравнение можно
решить точно только для атома водорода
при использовании сферических координат
и для иона
![]() в эллиптических координатах. Во всех
остальных случаях для решения применяются
приближенные методы.
в эллиптических координатах. Во всех
остальных случаях для решения применяются
приближенные методы.
ПРИМЕНЕНИЕ УРАВНЕНИЯ ШРЁДИНГЕРА


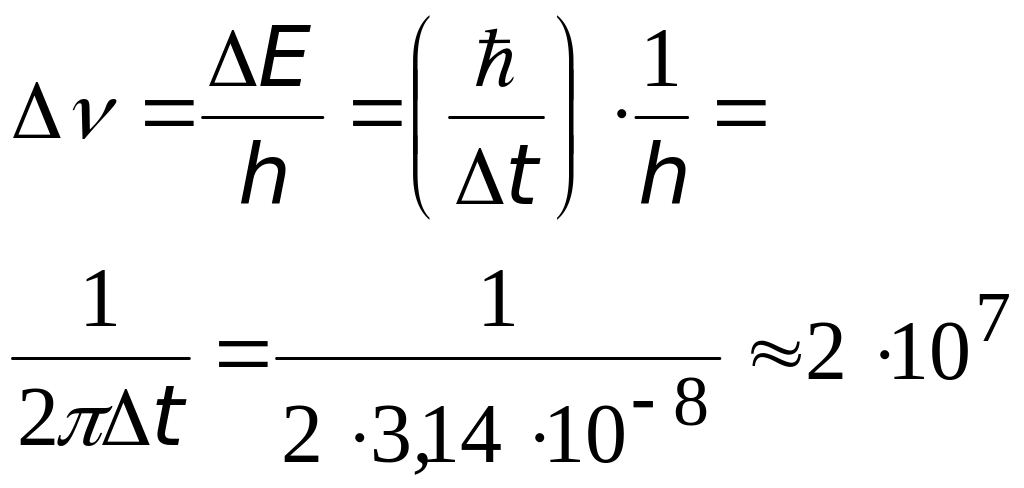 Гц
Гц