
- •В.4 Матрицы и операции над ними
- •В.5 ,6 Определители, их свойства и вычисление
- •Решение произвольных линейных систем
- •В 11. Векторы в пространстве: линейные операции над векторами в геометрической форме,проекция вектора на ось
- •Свойства непрерывных функций
- •. Правило Лопиталя. Формула Тейлора
- •План исследования функции и построения графика
В.5 ,6 Определители, их свойства и вычисление
Каждой квадратной матрице A порядка n можно поставить в соответствие единственное число, которое вычисляется по определенному правилу. Это число называется определителем (или детерминантом) матрицы A и обозначается |A|, или det A, или Δ(A). Порядок матрицы A является и порядком ее определителя. Определители порядка 1-3 определяются, соответственно, равенствами:
![]() ,
,
![]() ,
(3)
,
(3)
 .
.
Минором
Mij
элемента
aij
,
![]() ,
называется определитель
(n-1)-го
порядка, который состоит из элементов
матрицы, полученной из данной после
«вычеркивания» i-
той строки и j-того
столбца.
,
называется определитель
(n-1)-го
порядка, который состоит из элементов
матрицы, полученной из данной после
«вычеркивания» i-
той строки и j-того
столбца.
Алгебраическим
дополнением
элемента aij
называется
число
Аij=(-1)i+jMij.
Определитель
порядка n,
где
![]()
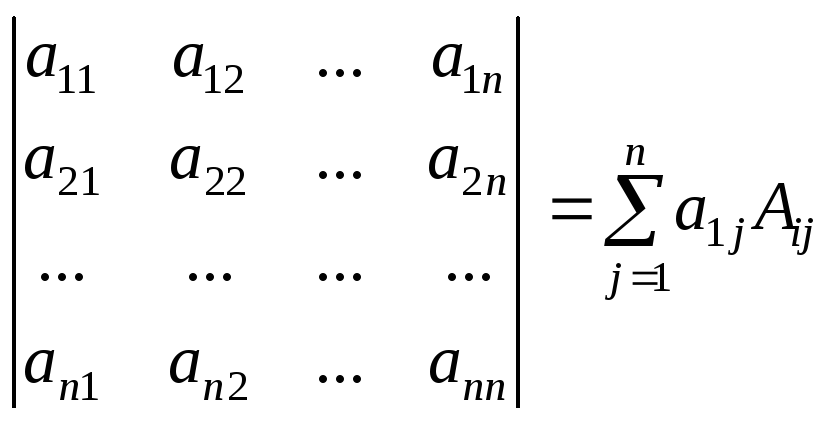 ,
определяется как число.
,
определяется как число.
Последнее равенство называют разложением определителя по элементам первой строки. Оно есть обобщение равенств (3).
Свойства определителей:
1)
![]() ;
;
2)
![]() ;
;
3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;
4) перестановка двух строк (столбцов) меняет знак определителя на противоположный;
5) |A|=0, если выполняется одно из следующих условий:
-
в определителе есть нулевая строка (нулевой столбец),
-
в определителе есть пропорциональные строки (столбцы),
-
в определителе есть строки (столбцы), являющиеся линейной комбинацией соответствующих элементов других строк (столбцов);
6) если к элементам одной строки (столбца) определителя прибавить линейную комбинацию соответствующих элементов других строк (столбцов), то значение определителя не изменится.
Основные методы вычисления определителей.
1. Для определителей 3-го порядка удобно использовать правило треугольников, которое схематично можно изобразить следующим образом:
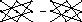
Линии соединяют по три элемента, которые умножаются, а затем произведения складываются.
2. Определитель порядка n может быть вычислен разложением по любой строке (столбцу):
![]() .
.
3. Метод эффективного понижения порядка определителя: используя свойства определителя, его преобразуют к такому виду, чтобы все элементы некоторой строки (столбца) определителя, кроме одного, были нулями, затем вычисляют определитель разложением по этой строке (столбцу).
4. Метод приведения к треугольному или диагональному виду с использованием свойств определителя, когда определитель равен произведению диагональных элементов.
.
В. 7 Обратная матрица. Ранг матрицы
Произведением
матрицы Al×m
на матрицу Bm×n
называется матрица
![]() элементы которой
элементы которой
![]() .
.
Для
получения элемента
![]() матрицы – произведения умножают
последовательно каждый элемент
матрицы – произведения умножают
последовательно каждый элемент
![]() строки
матрицы А
на
каждый элемент j-го
столбца матрицы
В и
находят сумму этих произведений.
строки
матрицы А
на
каждый элемент j-го
столбца матрицы
В и
находят сумму этих произведений.
Свойства операции умножения матриц:
В общем случае из
существования AB
не следует существование BA.
Даже если оба эти произведения определены,
они не всегда равны. Матрицы, для которых
![]() называются коммутативными.
называются коммутативными.
Квадратная матрица
B,
удовлетворяющая совместно с
заданной матрицей A
того же порядка равенствам
![]() называется обратной
матрицей
к A
и обозначается A–1.
Обратная матрица A–1
существует при условии, что
A
– невырожденная матрица,
т. е.
называется обратной
матрицей
к A
и обозначается A–1.
Обратная матрица A–1
существует при условии, что
A
– невырожденная матрица,
т. е.
![]()
Обратную матрицу можно вычислить следующими способами.
1-й способ. Используют формулу
![]() (4)
(4)
где С – матрица, составленная из алгебраических дополнений соответствующих элементов матрицы A.
2-й способ.
Для данной матрицы A
n-го
порядка строится прямоугольная размера
![]() матрица
матрица
![]() путем приписывания к A
справа единичной матрицы n-го
порядка; затем с помощью элементарных
преобразований над строками матрица
путем приписывания к A
справа единичной матрицы n-го
порядка; затем с помощью элементарных
преобразований над строками матрица
![]() приводится к виду
приводится к виду
![]() .
Тогда
.
Тогда
![]()
Рангом матрицы
A
размера
![]() называется максимальный
порядок
называется максимальный
порядок
![]() отличных от нуля ее миноров. При этом
любой ненулевой минор порядка
отличных от нуля ее миноров. При этом
любой ненулевой минор порядка
![]() называется базисным
минором
матрицы A.
называется базисным
минором
матрицы A.
Основные методы нахождения ранга матрицы A.
Метод окаймляющих миноров
Если в матрице A
найден ненулевой минор Mk
порядка k,
![]() а все окаймляющие
его миноры
а все окаймляющие
его миноры
![]() )-го
порядка равны нулю,
то ранг матрицы равен k
(
)-го
порядка равны нулю,
то ранг матрицы равен k
(![]() ).
).
Метод элементарных преобразований
Используя элементарные преобразования строк, матрицу приводят к трапециевидной или треугольной форме, далее ранг находят по определению.
Как частный случай последнего метода, может быть рассмотрен метод нулей и единиц: элементарными преобразованиями строк матрицу приводят к эквивалентной, состоящей или из нулевых строк и столбцов, или из строк и столбцов, в которых содержится ровно одна единица, а остальные элементы – нулевые. Количество единиц в такой матрице равно ее рангу.
В.8,9,10Системы линейных уравнений
Система линейных алгебраических уравнений (или линейная система) имеет вид:
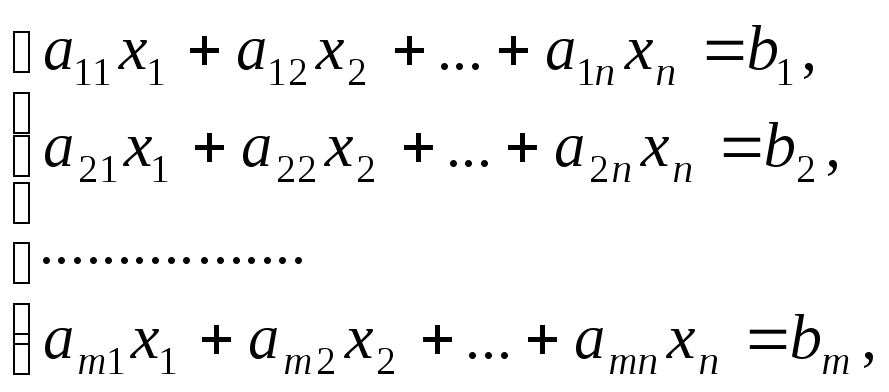
где aij и bj –заданные числа.
Систему (17) можно записать в матричной форме
![]() (8)
(8)
где А – матрица системы, состоящая из коэффициентов;
B – матрица-столбец свободных членов;
X
– матрица-столбец неизвестных,т. е.
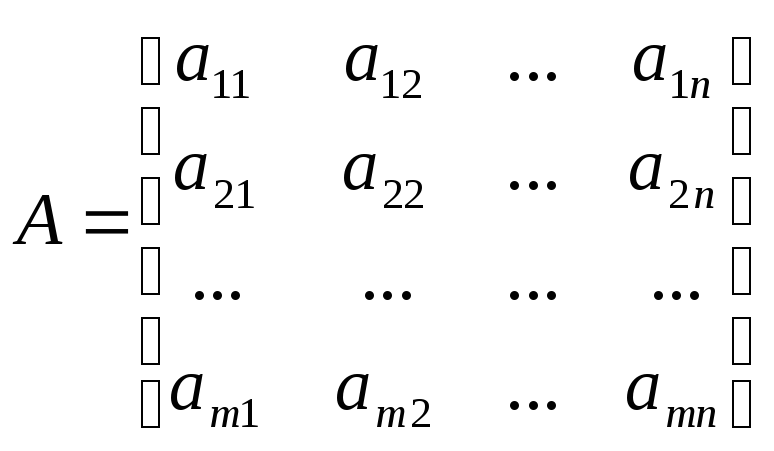 ,
, ,
,
 .
.
Решением
системы (7) называется совокупность n
чисел
![]() ,
которые после подстановки в уравнения
системы вместо соответствующих
неизвестных обращают каждое уравнение
системы в верное числовое тождество.
,
которые после подстановки в уравнения
системы вместо соответствующих
неизвестных обращают каждое уравнение
системы в верное числовое тождество.
Система (7) называется совместной, если у нее существует хотя бы одно решение, в противном случае она называется несовместной. Совместная система (7) называется определенной, если она имеет одно решение и неопределенной, если более одного решения. Две системы называются эквивалентными (равносильными), если множества их решений совпадают.
Ответ на вопрос о совместимости системы дает теорема Кронекера-Капелли: для того чтобы система (7) была совместной, необходимо и достаточно, чтобы
![]()
где
![]() – расширенная
матрица системы
(7), т.е. матрица свободных членов.
– расширенная
матрица системы
(7), т.е. матрица свободных членов.
Рассмотрим систему
![]() ,
имеющую вид:
,
имеющую вид:
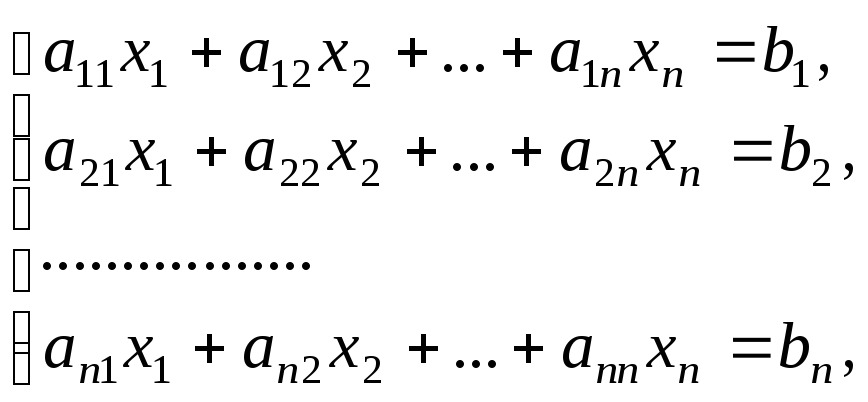 (9)
(9)
Определителем
системы
(9) называется определитель
матрицы этой системы (состоящий из
коэффициентов:
![]() ,
Если
,
Если
![]() то система называется невырожденной;
если
то система называется невырожденной;
если
![]() - вырожденной.
- вырожденной.
Методы решения
невырожденных систем
используются для решения линейных
систем (9), состоящих из n
уравнений с n
неизвестными
из которых
![]() .
.
Метод обратной матрицы состоит в решении матричного уравнения (8) по формуле
![]() (10)
(10)
Метод Крамера: для нахождения неизвестных необходимо использовать формулы
![]()
![]() (11)
(11)
где
![]() – определитель, получаемый из определителя
– определитель, получаемый из определителя
![]() системы (8) заменой i-го
столбца столбцом свободных членов.
системы (8) заменой i-го
столбца столбцом свободных членов.
Формулы (11) называются формулами Крамера.
