Решение произвольных линейных систем

Метод Гаусса используется в общем случае для систем вида (7) (вырожденных и невырожденных). С помощью элементарных преобразований над строками расширенную матрицу системы (7) приводят к виду:

Соответствующая ей система, равносильная (7), примет вид:

(12)

Если хотя бы одно из чисел b_{r + 1}, … b_m отлично от нуля, то система (11), а значит, и исходная система (7) несовместны.

Если b_{r + 1} = … = b_m = 0, то система (11) позволяет получить явное выражение для базисных неизвестных x₁, …, x_r через свободные неизвестные x_{r + 1}, …, x_n. Получаем бесконечное множество решений.

Если r = n, то свободные неизвестные отсутствуют, а значит, системы (11) и (7) имеют единственное решение.

На практике обычно обходятся приведением матрицы системы (7) к треугольной или трапециевидной форме, после чего значения базисных переменных ищутся в обратном порядке.

В 11. Векторы в пространстве: линейные операции над векторами в геометрической форме,проекция вектора на ось

Векторы называются компланарными, если они лежат в параллельных плоскостях (или в одной плоскости). Для трех некомпланарных векторов справедливо сложение по правилу параллелепипеда:

где – диагональ параллелепипеда, построенного на векторах с общим началом, имеет то же начало (рис. 1).

Рис. 1.

Вектор может задаваться также точкой начала и конца , обозначают .

Геометрической проекцией вектора на ось l называется вектор , где и – основания перпендикуляров, опущенных на ось из точек A и B соответственно (рис. 2).

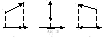
Рис. 2.

Если то является геометрической проекцией вектора на ось l, что обозначается .

Алгебраической проекцией (просто проекцией) вектора на ось l называется число которое определяется следующим образом:

Символ обозначают проекцию вектора на направление вектора т. е. на ось, определяемую ортом

Свойства проекции вектора на ось:

1) ;

2)

3)

4) .

В. 12 Скалярное произведение двух векторов в пространстве определяется аналогично случаю на плоскости:

.

Формула скалярного квадрата:

.

Справедлива формула, связывающая скалярное произведение векторов и проекции этих векторов:

. (1)

В.15 Линейная зависимость векторов. Действиянад векторами в координатной форме

Векторы называются линейно независимыми, если равенство

справедливо тогда и только тогда, когда В противном случае эти векторы называются линейно зависимыми. Для того чтобы векторы были линейно зависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.

Упорядоченная тройка ненулевых линейно-независимых векторов образует базис в трехмерном пространстве. Любой вектор пространства единственным образом может быть разложен по базисным векторам, т.е. представлен в виде

где – координаты вектора в базисе (записывают: ).

В пространстве линейная независимость векторов равносильна их некомпланарности, т.е. любые три некомпланарных вектора, взятые в определенном порядке, образуют базис.

Пусть задана тройка некомпланарных векторов. Совместим начала этих векторов. Если кратчайший поворот вектора до направления вектора , наблюдаемый с конца вектора совершается против часовой стрелки, то тройка векторов называется правой. В противном случае – левой. Всюду далее рассматриваются правые тройки базисных векторов.

Совокупность базисных векторов и их общего начала образуют, аффинную систему координат в пространстве. Координаты векторов в таком случае называют аффинными.

Если даны два вектора и в некотором базисе, то

тогда и только тогда, когда

(2)

(3)

В случае, когда базисные векторы попарно перпендикулярны, система координат называется прямоугольной декартовой. Если добавить, кроме того, условие нормированности базисных векторов (т.е. их единичную длину), то такой базис называют ортонормированным и обозначают : Прямоугольные декартовы координаты вектора является его проекциями на вектора соответственно.

Если точка M имеет прямоугольные декартовы координаты x, y, z в системе координат с началом в точке O(0, 0, 0) и базисом , то соответствующий радиус-вектор

Если и , то

.

Линейные операции для векторов и в координатной форме и их скалярное произведение вычисляются по формулам:

; (4)

(5)

(6)

; (7)

. (8)

Направляющими косинусами вектора называются величины , где углы, которые образует вектор соответственно с осями . Их вычисляют по формулам:

(9)

Если единичный вектор, то .

Координаты точки C, делящей отрезок AB в отношении , можно найти по формулам:

В.13 Векторное произведение

Векторным произведением двух векторов и называется вектор, удовлетворяющий следующим условиям:

1) ;

2)

3) тройка векторов – правая.

Векторное произведение обозначают также

Если хотя бы один из векторов или нулевой, то

Геометрический смысл векторного произведения состоит в том, что длина этого вектора численно равна площади параллелограмма, построенного на векторах и :

.

Физический смысл векторного произведения состоит в том, что момент силы приложенной к точке A, относительно точки O есть векторное произведение векторов и т. е.

.

Свойства векторного произведения:

1) ;

2) ;

3) ;

4) при тогда и только тогда, когда векторы и коллинеарны.

Если и то

Последнюю формулу удобно записать в виде формального определения третьего порядка:

В.14. Смешанное произведение векторов

Смешанным произведением трех векторов и называется число, определяемое соотношением

.

Если хотя бы один из векторов – нулевой, то их смешанное произведение равно нулю.

Геометрический смысл смешанного произведения векторов состоит в том, что его абсолютное значение равно объему V параллелепипеда, построенного на векторах приведенных к общему началу:

.

Свойства смешанного произведения

1) ;

2) ;

;

3) , где

4) при тогда и только тогда, когда – компланарные векторы;

5) векторы образуют базис в трехмерном пространстве при условии

6) если то векторы образуют правую тройку; если – левую.

В случае, когда векторы заданы в ортонормированном базисе координатами их смешанное произведение может быть найдено по формуле . (10)

Плоскость в пространстве

1. Положение плоскости P в пространстве относительно прямоугольной системы координат Oxyz однозначно определено, если задан радиус-вектор некоторой фиксированной точки и два некомпланарных вектора и , параллельных данной плоскости. В этом случае равенство где – радиус-вектор произвольной точки называется векторно-параметрическим уравнением плоскости P. Записав его в координатной форме получим параметрические уравнения плоскости.

2. Эту же плоскость можно задать одним из уравнений:

(1)

справедливость которых обусловлена условием компланарности векторов , и .

3. Координаты векторов и могут быть найдены, если известны три точки плоскости P, не лежащие на одной прямой:

В этом случае , . В результате имеем уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой.

4. Если известны точки пересечения плоскости P с координатными осями, т. е. M₀(a, 0, 0), M₁(0, b, 0), M₂(0, 0, c), то справедливо уравнение «в отрезках»:

5. Положение плоскости P в пространстве однозначно определено и в том случае, когда задан нулевой нормальный вектор и точка Условия перпендикулярности векторов и позволят перейти к векторному уравнению а затем к его координатной форме записи:

(2)

После преобразования последнего уравнения приходим к общему уравнению плоскости P:

где

6. Если в качестве нормального вектора плоскости P взять единичный вектор направленный из начала координат в сторону плоскости, то где Тогда справедливо нормальное уравнение плоскости

где – расстояние от начала координат до плоскости.

Величина , где называется отклонением точки от плоскости . При этом если и O(0, 0, 0) лежат по одну сторону от плоскости, – если лежат по разные, если Расстояние от точки до плоскости равно абсолютному значению ее отклонения, т. е.

.От общего уравнения плоскости к нормальному можно перейти с помощью умножения на нормирующий множитель

Значит, расстояние от точки до плоскости заданной общим уравнением может быть найдено по формуле

Угол между плоскостями в пространстве определяется по косинусу угла между нормальными векторами и этих плоскостей:

Уравнение прямой в пространстве. Взаимное

расположение прямых

Положение прямой в пространстве относительно прямоугольной системы координат однозначно определено, если известны координаты ее направляющего вектора и некоторой фиксированной точки этой прямой. Тогда радиус-вектор произвольной точки M, лежащей на прямой, может быть представлен в виде

где – радиус-вектор точки Полученное веккторно-параметрическое уравнение в координатной форме равносильно трем параметрическим уравнениям:

Исключая параметр t, придем к параметрическим уравнениям:

Прямую в пространстве можно задать и как линию пересечения двух плоскостей, заданных общими уравнениями, т. е. системой линейных уравнений:

где коэффициенты при неизвестных не являются пропорциональными.

Расстояние от точки до прямой L с направляющим вектором и проходящей через точку может быть найдено по формуле

где и – радиус-векторы точек и соответственно.

Эту формулу можно использовать и для нахождения расстояния между параллельными прямыми.

Если прямые и являются скрещивающимися, то расстояние между ними

где и – радиус-векторы точек и принадлежащих прямым и соответственно, а векторы и – их направляющие векторы.

О взаимном расположении двух прямых в пространстве можно судить по их направляющим векторам.

Прямые параллельны при условии коллинеарности их направляющих векторов (координаты пропорциональны).

Прямые перпендикулярны при условии перпендикулярности их направляющих векторов (скалярное произведение равно 0).

Угол между прямыми можно определить через косинус угла между направляющими векторами.

Прямые лежат в одной плоскости при условии компланарности их направляющих векторов и вектора где и – точки этих прямых (смешанное произведение равно 0).

Расстояние от точки до прямой L

где – направляющий вектор, – точка прямой.

Прямая и плоскость в пространстве

Пусть прямая L задана каноническими уравнениями:

где а плоскость P – общим:

где

Тогда взаимное расположение прямой L и плоскости P в пространстве можно определить по направляющему вектору прямой L и нормальному вектору плоскости P.

1.

2.

3.

4. координаты точки пересечения могут быть найдены следующим образом. От канонических уравнений прямой следует перейти к параметрическим, после чего подставить найденные значения в уравнение плоскости. Разрешить полученное уравнение относительно параметра t. Найденное значение подставить в параметрические уравнения, что позволит найти значения которые и будут координатами искомой точки пересечения прямой L и плоскости P.

Углом между и плоскостью называется угол между прямой и ее ортогональной проекцией на плоскость, т. е.

.

Поверхности второго порядка

Алгебраической поверхностью второго порядка называется поверхность S, общее уравнение которой в декартовой прямоугольной системе координат относительно текущих координат имеет вид

где коэффициенты при одночленах второй степени одновременно не равны нулю.

Эти уравнения определяют тип поверхности и называются каноническими.

1. Эллипсоид:

2. Гиперболоид

1) эллиптический:

2) гиперболический:

3. Конус второго порядка:

4. Параболоид

5. Цилиндр

1) эллиптический:

2) гиперболический:

3) параболический:

Основным методом исследования формы поверхности является метод сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о виде поверхности. Таким образом изучаются основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.

При этом, когда в общем уравнении поверхности коэффициенты приведение к каноническому виду осуществляется с помощью метода выделения полных квадратов и параллельного переноса системы координат. При наличии же в общем уравнении поверхности смешанных произведений переменных приведение к каноническому виду опирается на теорию квадратичных форм.

В любом случае, общее уравнение поверхности может быть приведено к уравнениям, задающим так называемые вырожденные поверхности. Приведем примеры таких случаев.

1. – пустое множество точек (мнимый эллипсоид);

2. – точка (0, 0, 0);

3. – пустое множество точек

Предел функции в точке и на бесконечности

Определение по Коши

Число А называется пределом функции f(x) в точке х₀, если функция определена в некоторой выколотой окрестности точки х₀ и если для любого сколь угодно малого числа существует такое число что для всех х, удовлетворяющих условию

(1)

выполняется

(2)

Это записывают:

Число А называется пределом функции на бесконечности, если для любого существует число что для всех х, удовлетворяющих условию

выполняется неравенство

Это записывают:

().

Определение предела функции в точке (на бесконечности) по Гейне и по Коши эквивалентны.

Функция f(x) называется бесконечно большой при если для всякого числа М > 0 существует что для всех х, удовлетворяющих условию

()

выполняется неравенство

Это записывают:

.

Если f(x) – бесконечно большая функция при то она не имеет предела в этой точке (на бесконечности). Символ предела в данном случае используют лишь для обозначения.

Функция f(x) называется бесконечно малой при если

.

Свойства предела функции в точке

1. Если функция f(x) имеет предел в точке х₀, то существует окрестность этой точки (за исключением, быть может, самой точки х₀), на которой функция ограничена.

2. Если существует предел функции f(x) в точке х₀, равный то существует такая окрестность точки х₀, на которой функция имеет тот же знак, что и А.

3. Если функции f(x) и g(x) имеют пределы в точке х₀, то:

где (3)

(4

где (5)

Аналогичные свойства верны и для предела функции на бесконечности.

Если в результате непосредственного использования формул (3)–(5) возникает неопределенность типа то вначале необходимо тождественно преобразовать выражение, стоящее под знаком предела (то же для неопределенностей ).

Свойства бесконечно малых и бесконечно больших функций

1. Число А является пределом функции f(x) в точке х₀ тогда и только тогда, когда существует бесконечно малая функция при такая, что .

2. Сумма и произведение конечного числа бесконечно малых (бесконечно больших) функций при является бесконечно малой (бесконечно большой функцией).

3. Произведение бесконечно малой при функции на ограниченную функцию является бесконечно малой.

4. Частное при делении постоянной С, на бесконечно малую при является бесконечно большой при

5. Частное при делении постоянной С на бесконечно большую при является бесконечно малой при

При вычислении пределов функций удобно применять метод замены переменной, т.е. , где , если .

Замечательные пределы

При вычислении пределов в случае неопределенностей часто используют специальные формулы, которые называются замечательными пределами.

Первый замечательный предел

(7)

Как следствие формулы (7) справедливы формулы

Второй замечательный предел

(8)

Третий замечательный предел

(9)

в частности,

Четвертый замечательный предел

(10)

в частности,

Пятый замечательный предел

(11)

Указанные формулы (7)–(11) замечательных пределов обобщаются на любую функцию u(x), стоящую вместо независимой переменной х при условии, что если (или ) во всех формулах кроме (8), в которых

Обобщенная таблица замечательных пределов

;

; ; (12)

; ; (13)

; ; (14)

. (15)

При использовании обобщенных форму на практике вместо (под знаком предела пишут указанное в условии: .

Все приведенные формулы обобщенной таблицы замечательных пределов (кроме формул (12)) раскрывают неопределенность типа . Формулы (12) раскрывают неопределенность типа .

Эквивалентность функции

Две функции и называются эквивалентными бесконечно малыми, при , если

,

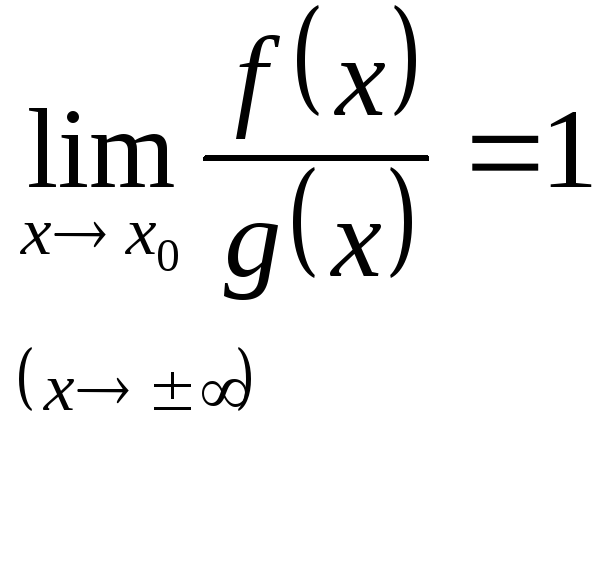это записывают при .

При вычислении пределов функций в точке и на бесконечности удобно пользоваться следующей теоремой:

Если , и - некоторые функции, определенные в

окрестности точки (на числовой полуоси) и при

, то

. (16)

Формула (16) показывает, что в произведении можно заменять функцию – сомножитель на эквивалентную ей – более простую для вычисления предела.

Таблица эквивалентных бесконечно малых

Пусть , если . Тогда справедливы следующие эквивалентности:

; (17)

; (18)

; (19)

; (20)

; (21)

(22)

(23)

(24)

Односторонние пределы: Асимптоты графика функции.

Левой (правой) полуокрестностью точки называется произвольный интервал, где слева (справа).

Число А называется пределом функции в точке слева (справа), если функция определена в некоторой левой (правой) полуокрестности точки и если для любого существует такое, что для всех , удовлетворяющих условию , выполняется неравенство

.

В этом случае пишут

Пределы слева и справа называются односторонними пределами. Если, то односторонние пределы обозначают , .

Функция имеет предел в точке тогда и только тогда, когда в этой точке существуют оба односторонние предела, равные между собой.

В этом случае их общее значение и является пределом функции в точке

.

Асимптота графика функции - это прямая линия, к которой неограниченно приближается график данной функции, когда его точка неограниченно удаляется от начала координат.

Различают горизонтальную, вертикальную и наклонную асимптоты.

Прямая называется вертикальной асимптотой, графика функции , если

или .

В случае вертикальной асимптоты функция является бесконечно большой в точке .

Прямая называется горизонтальной асимптотой графика функции , если .

Вертикальные асимптоты могут существовать у функций, которые определены не на всей числовой прямой.

Если областью определения функции является вся числовая прямая, то у функции нет вертикальных асимптот.

Прямая называется наклонной асимптотой графика функции , при , если

.

Для нахождения коэффициентов и b применяют следующие формулы:

(25)

(26)

Если хотя бы один из этих пределов равен или не существует, то у функции наклонных асимптот нет.

Если , , то прямая является горизонтальной асимптотой. Горизонтальная асимптота – это частный случай наклонной асимптоты.

Заметим, что наклонных асимптоты у функции может быть не больше двух, а вертикальных может быть сколько угодно.

. Непрерывность функции. Классификация

точек разрыва.

Функция называется непрерывной в точке , если она определена в этой точке в некоторой ее окрестности и

(27)

Если функция непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.

Существуют и другие определения непрерывности функции в точке. Функция называется непрерывной в точке , если она определена в этой точке и в некоторой ее окрестности и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке:

(28)

Непрерывность функции в точке определяется также на основе односторонних предметов.

Функция называется непрерывной в точке , если она определена в этой точке и некоторой ее окрестности и существует односторонние пределы (конечные) такие, что

(29)