
- •В.4 Матрицы и операции над ними
- •В.5 ,6 Определители, их свойства и вычисление
- •Решение произвольных линейных систем
- •В 11. Векторы в пространстве: линейные операции над векторами в геометрической форме,проекция вектора на ось
- •Свойства непрерывных функций
- •. Правило Лопиталя. Формула Тейлора
- •План исследования функции и построения графика
. Правило Лопиталя. Формула Тейлора
В случае
неопределенностей
![]() и
и
![]() при вычислении пределов часто бывает
полезным применять правило Лопиталя,
которое задается следующей Теоремой.
при вычислении пределов часто бывает
полезным применять правило Лопиталя,
которое задается следующей Теоремой.
Теорема 1.
Пусть функции
![]() и
и
![]() удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1) определены и
дифференцируемы на интервале (a; b),
за исключением быть может точки
![]() причем
причем
![]() и
и
![]()
![]()
2)
![]() (либо
(либо
![]() );
);
3) существует предел
![]() тогда существует предел отношений
функций
тогда существует предел отношений
функций
![]() причем
причем
![]() (17)
(17)
Правило Лопиталя можно использовать последовательно несколько раз.
Аналогичное правило
верно в случае
![]()
Если при вычислении
пределов возникает неопределенность
иного вида, то в начале их необходимо
свести к неопределенности вида
![]() ,
,
![]() ,
а затем использовать правило Лопиталя.
,
а затем использовать правило Лопиталя.
В частности,
выражения, которые приводят к
неопределенностям
![]()
![]() тождественно преобразуют к такому
выражению, которое приводят к
неопределенности
тождественно преобразуют к такому
выражению, которое приводят к
неопределенности
![]() или
или
![]() .
Неопределенность вда
.
Неопределенность вда
![]()
![]()
![]() возникают при рассмотрении функции
типа
возникают при рассмотрении функции
типа
![]() С помощью тождества
С помощью тождества
![]() (18)
(18)
они сводятся к
неопределенности
![]()
Если функция
![]() имеет в некоторой окрестности точки
имеет в некоторой окрестности точки
![]() производные до
производные до
![]() -го
порядка включительно, то при
-го
порядка включительно, то при
![]() верна формула Тейлора
верна формула Тейлора
 (19)
(19)
где
![]() – остаточный член формулы Тейлора.
– остаточный член формулы Тейлора.
Существует несколько форм записи остаточного члена. В частности, в форме Логранжа:
![]()
![]() .
.
Если в формуле
Тейлора
![]() получим частный вид формулы Тейлора,
называемый формулой Маклорена:
получим частный вид формулы Тейлора,
называемый формулой Маклорена:
![]()
где
![]()
![]()
Верны следующие формулы Маклорена:
![]() (20)
(20)
где
![]()
![]()
где
![]()
![]() (21)
(21)
где
![]()
![]() (22)
(22)

Формулы Маклорена могут быть использованы в приближенных вычислениях. При этом абсолютная погрешность приближения в случае чередования знаков в формуле Маклорена не превосходит абсолютной величины первого отображаемого слагаемого.
Исследование функций. Наибольшее
и наименьшее значение функций на промежутке
Всюду далее функция
![]() определена на рассматриваемых промежутках.
определена на рассматриваемых промежутках.
Теорема 1.
Дифференцируемая на
![]() функция (убывает) на этом интервале
тогда и только тогда, когда
функция (убывает) на этом интервале
тогда и только тогда, когда
![]()
![]()
![]()
Точка
![]() называется точкой локального максимума
(минимума) функции
называется точкой локального максимума
(минимума) функции
![]() ,
если существует некоторая окрестность
точки
,
если существует некоторая окрестность
точки
![]() такая, что для всех x
из этой окрестности выполняется
неравенство
такая, что для всех x
из этой окрестности выполняется
неравенство
![]()
![]() .
.
Значение
![]() называется локальным максимумом
(минимумом)
функции.
называется локальным максимумом
(минимумом)
функции.
Точки максимума или минимума функции называются точками экстремума (локального). Максимум и минимум называются экстремумом функции.
Теорема 2 (необходимое условие существования экстремума функции).
Если в точке
![]() функция
функция
![]() достигает экстремума, то ее производная
в этой точке равна нулю или не существует.
Точки, в которых производная функции
достигает экстремума, то ее производная
в этой точке равна нулю или не существует.
Точки, в которых производная функции
![]() обращается в нуль или не существует,
называют критическими.
Исследование функции на экстремум
начинается с нахождения критических
точек. Однако не в каждой критической
точке существует экстремум. Для того,
чтобы определить точки экстремума
используют достаточные условия (признаки
экстремума).
обращается в нуль или не существует,
называют критическими.
Исследование функции на экстремум
начинается с нахождения критических
точек. Однако не в каждой критической
точке существует экстремум. Для того,
чтобы определить точки экстремума
используют достаточные условия (признаки
экстремума).
Теорема 3 (первый признак экстремума функции).
Пусть
![]() – критическая точка непрерывной функции
– критическая точка непрерывной функции
![]() .
.
Если
в некоторой окрестности точки
![]() выполняется условие
выполняется условие
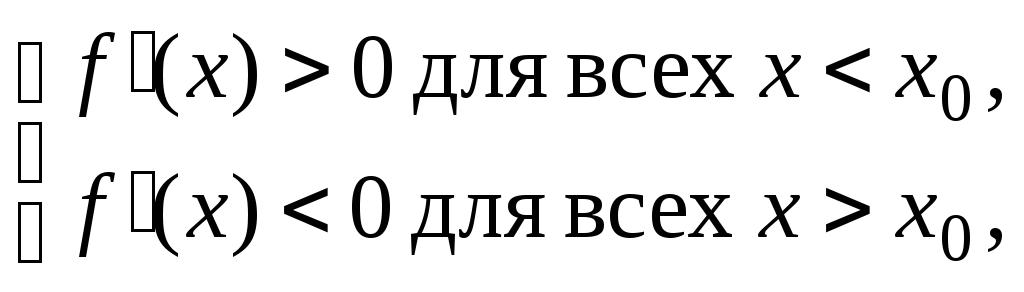
то
![]() – точка локального максимума;
– точка локального максимума;
если выполняется условие
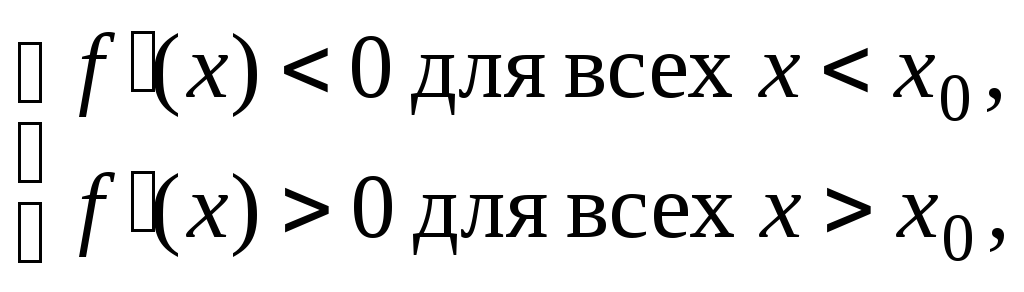
то
![]() – точка локального минимума.
– точка локального минимума.
Если производная
![]() имеет один и тот же знак в левой и правой
полуокрестности точки
имеет один и тот же знак в левой и правой
полуокрестности точки
![]() ,
то
,
то
![]() не является точкой экстремума.
не является точкой экстремума.
Теорема 4 (второй признак экстремума функции).
Пусть
![]() – критическая точка функции
– критическая точка функции
![]() ,
дважды дифференцируемой в окрестности
точки
,
дважды дифференцируемой в окрестности
точки
![]() .
Тогда
.
Тогда
![]() является точкой локального минимума
функции
является точкой локального минимума
функции
![]() ,
если
,
если
![]() и точкой локального максимума, если
и точкой локального максимума, если
![]()
Теорема 5 (третий признак экстремума функции).
Пусть
![]() – n
раз непрерывно дифференцируемая в
критической точке
– n
раз непрерывно дифференцируемая в
критической точке
![]() функция и
функция и
![]()
![]() Тогда:
Тогда:
1) если n
– четное и
![]() то
то
![]() – точка локального максимума;
– точка локального максимума;
2) если n
– четное и
![]() то
то
![]() – точка локального минимума;
– точка локального минимума;
3) если n
– не четное, то
![]() не является точкой локального экстремума.
не является точкой локального экстремума.
Точка
![]() называется точкой
глобального максимума (минимума)
функции
называется точкой
глобального максимума (минимума)
функции
![]() на некотором промежутке, если для любой
точки x
из этого промежутка выполняется
неравенство
на некотором промежутке, если для любой
точки x
из этого промежутка выполняется
неравенство
![]()
![]() .
.
Точки глобального максимума и минимума называются точками глобального экстремума. Значения функции в этих точках называются соответственно глобальным максимумом (наибольшим значением) и глобальным минимумом (наименьшим значением).
Теорема 5
(Вейерштрасса). Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
то она достигает на нем своих наименьшего
и наибольшего значений
,
то она достигает на нем своих наименьшего
и наибольшего значений
Непрерывная на
отрезке
![]() достигает наименьшего (наибольшего)
значений либо на концах отрезка, либо
в точках ее локального экстремума.
достигает наименьшего (наибольшего)
значений либо на концах отрезка, либо
в точках ее локального экстремума.
Для отыскания
глобальных экстремумов функции
![]() на отрезке
на отрезке
![]() необходимо:
необходимо:
1) найти производную
![]()
2) найти критические точки функции;
3) найти значения
функции на концах отрезка, т. е.
![]() и
и
![]() а также в критических точках, принадлежащих
а также в критических точках, принадлежащих
![]()
4) из всех полученных значений функции определить наибольшее и наименьшее ее значения.
График функции
![]() называется вогнутым
(выпуклым вниз) на
называется вогнутым
(выпуклым вниз) на
![]() ,
если дуга кривой
,
если дуга кривой
![]() на этом интервале расположена выше
любой касательной проведенной к графику
этой функции (рис. 1).
на этом интервале расположена выше
любой касательной проведенной к графику
этой функции (рис. 1).

Рис. 1.
График функции
![]() называется выпуклым
(выпуклым вверх) на
называется выпуклым
(выпуклым вверх) на
![]() ,
если дуга кривой
,
если дуга кривой
![]() на этом интервале расположена ниже
любой касательной проведенной к графику
этой функции (рис. 2).
на этом интервале расположена ниже
любой касательной проведенной к графику
этой функции (рис. 2).

Рис. 2.
Теорема 6.
Если функция
![]() дважды дифференцируема на
дважды дифференцируема на
![]() и
и
![]()
![]() всюду на этом интервале, то график
функции вогнут (выпуклый) на
всюду на этом интервале, то график
функции вогнут (выпуклый) на
![]() .
.
Точка
![]() така, что график функции
така, что график функции
![]() меняет выпуклость на вогнутость или
наоборот, проходя через
меняет выпуклость на вогнутость или
наоборот, проходя через
![]() ,
называется точкой
перегиба
(рис. 3)
,
называется точкой
перегиба
(рис. 3)

Рис. 3.
Для нахождения
точек перегиба вначале находят критические
точки 2-го рода
– те значения x,
для которых
![]() или
или
![]() не существует. Далее используют
достаточные условия перегиба.
не существует. Далее используют
достаточные условия перегиба.
Теорема 7 (достаточные условия перегиба).
Если
для функции
![]() вторая производная
вторая производная
![]() в некоторой точке
в некоторой точке
![]() обращается в нуль или не существует и
при переходе через нее
обращается в нуль или не существует и
при переходе через нее
![]() меняет свой знак, то
меняет свой знак, то
![]() – точка перегиба.
– точка перегиба.
