7. Комбинированный метод хорд и касательных.

Обладает более высокой сходимостью по сравнению с отдельно взятыми методами хорд и касательных за счет того, что на каждом шаге неподвижная граница метода хорд заменяется границей, найденном по методу касательных.

Тогда в силу сказанного расчетные формулы комбинированного метода хорд и касательных запишем в следующем виде:

(6)

Расчетные формулы комбинированного метода.

Вычисления следует прекратит на шаге к при выполнении условия:

и в качестве приближенного решения задачи следует принять любое число из отрезка .

Соотношение (6) получены при выполнении условий:

f ’(x) >0

f ’’(x)>0

Если же характер монотонности и выпуклости будет иным, то расчетные формулы комбинированного метода следует вывести вновь.

Условие сходимости комбинированного метода хорд и касательных имеет вид:

f ’(с)* f ’’(с)>0, где с – либо левая, либо правая граница. (7)

Та из границ, которая удовлетворяет условию сходимости (7) есть граница старта метода касательных

Метод итераций для линейных уравнений

Рассмотрим на примере СЛАУ, содержащей три уравнения с тремя неизвестными.

(1)

Необходимо определить корни системы 1 с точностью ε.

Приведем систему 1 к виду, удобному для итераций. Для этого выразим неизвестные, лежащие на главной диагонали.

Или, введя соответствующие сообщения, последнюю систему запишем в виде:

(2)

В дальнейшем верхним индексом будем обозначать не показатель степени, а номер итерации.

В качестве нулевого приближения выберем числа β_i, т.е.

Выбранные приближения подставим в правые части уравнений 2, вычислим примем как первое приближение:

Найденные первые приближения подставим вновь в уравнение 2:

Эти значения примем в качестве второго приближения.

Рассуждая аналогично, на шаге n получим:

(3)

3 – расчетные формулы метода итераций. Заметим, что соотношение 3 показывает, что каждое последующее приближение n определяется строго по предыдущему (n-1).

Описанная выше итерационная процедура оказывается сходящейся при увеличении числа n к точным решениям, если в каждой строке матрице коэффициентов А:

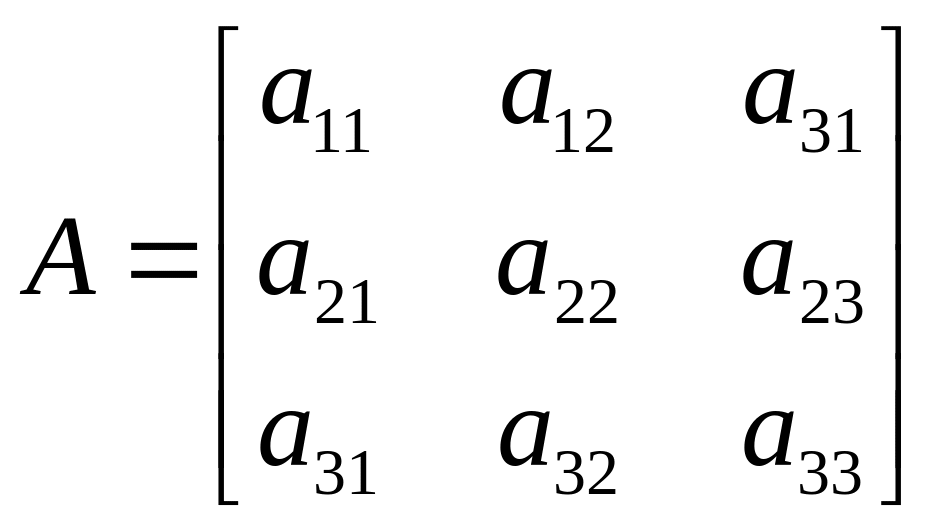
max по модулю оказывается элемент, лежащий на главной диагонали. Заданная точность будет достигнута при выполнении условия:

и в качестве , , решения следует выбрать эту тройку чисел.

Метод Гаусса для линейных уравнений

Рассмотрим метод Гаусса на примере линейной системы, содержащей три уравнения с тремя неизвестными.

(1)

Из курса математики корни системы уравнений не меняются при почленном суммировании уравнений, на число отличное от 0, при перестановке уравнений. В силу упомянутых выше трех свойств всегда можно предположить, что а₁₁≠0 для системы, имеющей единственное решение.

Решение системы виды:

(2)

Всегда можно определить как:

(3)

Целью метода Гаусса является приведение системы (1) к равносильному виду (2) с последующим определением корней исходной системы по формулам (3).

Систему (1) запишем в матричной форме, в которой под каждой строкой будем подразумевать некоторое уравнение системы (1).

(4)

В качестве первой ведущей строки выберите 1 строку матрицы (4), а в качестве 1 ведущего элемента выберем элемент а₁₁. Из второй строки, умноженной на а₁₁, вычтем ведущую строку, умноженную на а₂₁, и из третьей строки, умноженной на а₁₁, вычтем ведущую строку, умноженную на а₃₁. Получим:

(*)

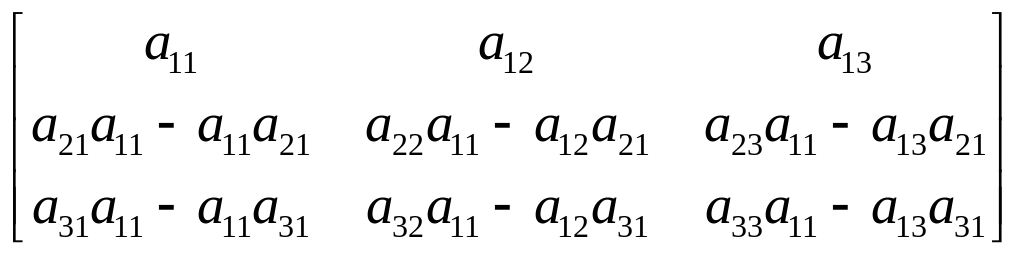
Или введя соответствующие обозначения …….

В силу упомянутых выше трех свойств всегда можно предположить, что а₂₂≠0. В качестве второй ведущей строки в последующей матрице примем вторую строку, а в качестве второго ведущего элемента элемент а₂₂.

Первую и вторую ведущие строки оставим без изменения, а из 3-ей строки, умноженной на вычтем 2-ую ведущую строку, умноженную на . Получим:

или введя обозначения

(5)

Матрица (5) соответствует по форме системе уравнений 2 и в силу равносильности полученных систем корни уравнений системы (1) могут быть найдены по формулам по форме совпадающим с соотношениями 3, что и позволяет решить исходную задачу.