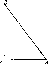ших классах на кружковых занятиях. Второй вариант аналитического введения тригонометрических функций - использование аппарата рядов, в настоящее время такой подход для средней школы представляется нереальным.

Более привычным для школы сегодня является второй путь - геометри­ческий, который существует и совершенствуется уже более ста лет. Имеется большое число разновидностей этого пути. Самый наглядный и простой из них является введение тригонометрических функций путем рассмотрения отноше­ний сторон в прямоугольном треугольнике. Основной недостаток такого опре­деления тригонометрических функций - затруднения, возникающие при пере­ходе к углам, большим прямого, и при переходе к тригонометрическим функ­циям числового аргумента. Попытки преодоления первой из этих трудностей привели к разнообразным по форме, но единым, по сути, подходам - через так называемые тригонометрические линии в круге, через отношения координат радиус-вектора, через проекции единичного вектора и т. п.

В дальнейшем мы будем рассматривать лишь второй путь, изучение кото­рого начинается в курсе геометрии основной школы.

2. Значение тригонометрических функций в школьном курсе математики и различные подходы к их изложению

Тригонометрические функции играют важную роль в математике и ее приложениях. Они описывают связи между сторонами и углами треугольников. Тригонометрические функции и их использование в курсе геометрии позволяет рассматривать понятие функции как важнейшее понятие математики, связывая тем самым курсы алгебры и геометрии. Велико значение тригонометрических функций в формировании научного мировоззрения: с их помощью геометриче­ские факты находят применение в практической деятельности, в частности при проведении различных измерительных работ на местности, они являются моде­лью многих периодических процессов (биение сердца, зависимость напряжения в металле от нагрузки на него и т. д.).

В учебной литературе существуют различные системы изложения триго­нометрических функций.

1. Ограничиваются рассмотрением тригонометрических функций острого угла прямоугольного треугольника. Такой подход был реализован в учебнике А. П. Киселева.

2. Вначале вводят тригонометрические функции острого угла прямо­угольного треугольника, доказывают несколько теорем с их использованием, затем распространяют понятие тригонометрических функций на множество уг­лов от 0° до 180°, и рассматривают их различные приложения. Такая система излагается в учебнике А. В. Погорелова.

В учебнике А. Д. Александрова и др. рассматриваются параллельно три­гонометрические функции острого и тупого углов.

3. Тригонометрические функции сразу рассматривают на множестве уг­лов, изменяющихся от 0° до 180°, затем частный случай от 0° до 90° -

248

Авторы учебников
и/и А. В. Погорелое	Л. С. Атанасян и др.
8 класс
| §7. Теорема Пифагора	Глава VII. Подобные треугольники § 4. Соотношения между сторонами и углами прямоугольного треугольника.
1 Косинус острого угла прямоугольного | ре-угольника, теорема о зависимости косинуса угла только от градусной ме­ры угла.	Синус, косинус и тангенс острого угла прямоугольного треугольника.
Георема Пифагора (использование ко­ей нуса угла для ее доказательства).	Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°.

249

3.	Определение синуса угла а, тангенса угла от (яг -острый угол) и теорема о зависимости их только от величины уг­ла а.
4.	Основные тригонометрические тожде- sina ,2 2 1 ства: tga = ; sin or + cos a-1; cosor 2 l 1 l l l + rg ar= 2 ;l+, 2 = . 2 ■ cos or tg a sm a
5.	Значения синуса, косинуса, тангенса некоторых углов. Формулы: sin (90° -а) = cos a, cos(90° -a) = sina.
6.	Изменение синуса, косинуса и тангенса при возрастании угла.
	§8. Декартовы координаты на плоскости
7.	Определение синуса, косинуса и тан­генса для любого угла от 0° до 180°.
	§10. Векторы
8.	Использование косинуса угла при изуче­нии скалярного произведения векторов.
	9 класс
	§12, Решение треугольников	Глава XI. Соотношения между сторона­ми и углами треугольника. Скалярное произведение векторов. §1. Синус, косинус и тангенс угла а (0° < or < 180°)
9.	Теорема косинусов а^2 = Ъ^2 +с^2 -2bccosA.	Основное тригонометрическое тождество. sin^2 а + cos^2 а -1. Формулы приведения sin (90° -а) = cos a, cos(90° -a) = sina.
10.	Теорема синусов а b с sin A sin В sin С	Формулы для вычисления координат точки.
11.	Соотношение между углами треуголь­ника и противолежащими сторонами.	§2. Соотношение между сторонами и углами треугольника
12.	Решение треугольников.	Теорема о площади треугольника S =—absinC. 2
	§13. Многоугольники	Теорема синусов а Ъ с sin A siпВ sin С

13.	Использование тригонометрических функций при изучении формул для ра­диусов вписанных и описанных окруж­ностей правильных многоугольников.	Теорема косинусов а^1 - Ъ^2 + с^2 - 2be cos А - обобщенная тео­рема Пифагора,
	§14. Площади фигур	Решение треугольников.
14.	Использование тригонометрических функций при выводе формул для вы­числения площади треугольника.

В учебнике А. В. Погорелова изложение тригонометрических функций осуществляется по схеме «от частного к общему», а в учебнике Л. С. Атанасяна и др. - «от общего к частному», причем в первом учебнике наблюдается связь из­ложения тригонометрических функций с изложением геометрического материала, тогда как во втором учебнике применение тригонометрических функций к обосно- манию геометрических зависимостей более ограничено, чем в первом. а) Введение понятий синуса, косинуса и тангенса острого угла прямоугольного треугольника Наиболее принципиальными вопросами методики изучения тригономет- рических функций острого угла прямоугольного треугольника являются: 1) инедение понятий синуса, косинуса и тангенса острого угла и 2) доказательство шниеимости их только от градусной меры угла. Перед введением понятий синуса и косинуса угла желательно выпол- шпъ упражнения на выделение катетов прямоугольных треугольников, приле- жащих к углу, противолежащих углу, на составление отношений катетов к ги- пок* пузе. После выполнения упражнений вводятся определения синуса, косинуса и I апгенса острого угла прямоугольного треугольника. Определение L Синусом острого угла прямоугольно- го треугольника называется отношение противолежащего катета к гипотенузе (рис. 95). Обозначение. sin а. Определение 2. Косинусом острого угла прямо- угольного треугольника называется отношение прилежа- щего катета к гипотенузе. Обозначение, cos а. Определениие 5. Тангенсом острого угла прямо- угольного треугольника называется отношение противо- лежащего катета к прилежащему. Обозначение, tga. не. 95	• л ^ВС S1ПЛ = —, АВ	(1)
	А ^ЛС cos А- , АВ	(2)
	а ^ВС tgA = . АС	(3)

251

3. Затем доказывается утверждение: если острый угол одного прямо- угольного треугольника равен острому углу другого прямоугольного треуголь- ника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны. Доказательство основано на первом признаке подобия треуголь- ников (В учебнике А. В. Погорелова аналогичное утверждение доказывается с помощью теоремы о пропорциональных отрезках). Действительно, пусть ABC и А \В\ С] - два прямоугольных треугольника с прямыми углами С и С\ и равными острыми углами А и А\. Треугольники ABC и А\В\С\ подобны по первому при-

* АВ ВС АС _тт знаку подобия треугольников, поэтому —- = = . Из этих равенств

А ^В j В _ЛС _х А₁С₁

ВС В С А С А С

следует, что — = —²—^L, то есть sin А = sin А_х. Аналогично — = —^L-Ч то есть

^J АВ А,В, АВ А_хВ_г

ВС в с

cos А = cos Аь и — = Ц то есть tg A =tgA\. Что и требовалось доказать.

АС А_ХС_Х

Из этого утверждения следует, что косинус угла (а также его синус) не зависит от расположения треугольника, а зависит только от градусной меры уг- ла. Доказательство независимости тангенса острого угла от размеров треуголь- ника следует из представления тангенса угла через отношение синуса и косину- са этого угла.

После доказательства этого утверждения необходимо выполнить с уча- щимися несколько упражнений на построение угла по заданному косинусу (си- нусу) этого угла.

Основное тригонометрическое тождество sin² А + cos² А = 1 получается из равенств (1) и (2).

. 2 j 2 _л ВС² АС² ВС² + АС²

sin А + cos А - —г + -

АВ² АВ² АВ²

По теореме Пифагора ВС² + АС² = АВ², поэтому sin² А + cos² А = 1.

После доказательства этих утверждений учащиеся находят сначала зна­чение синуса, косинуса и тангенса для углов 30° и 60°, а затем для угла 45°, при этом используются определения синуса, косинуса и тангенса угла, основное тригонометрическое тождество и теорема Пифагора.

В учебнике А. В. Погорелова понятие косинуса угла используется при доказательстве теоремы Пифагора, а в учебнике JL С. Атанасяна и др. теорема Пифагора к этому времени уже доказана и доказательство её основано на поня­тиях площади квадрата и прямоугольника.

Тригонометрические функции острого угла используются для решения прямоугольных треугольников. Они позволяют, зная одну из сторон прямо­угольного треугольника и острый угол, находить две другие стороны: зная две стороны, находить острые углы.

Доказательство утверждения о том, что для любого острого угла а sin(90°-a) = cosa, cos(90° -а) - sin а могут провести сами учащиеся, выполняя упражнение:

Упражнение. Дан прямоугольный треугольник ABC с острым углом а при вершине А. Напишите значение синуса и косинуса углов А и В, сравните их

252

и сделайте вывод.

В учебнике А. В. Погорелова рассматривается теорема об изменении sin a, cos а и tg а при возрастании угла а, в частности, об убывании cos а и ее доказательство. Она может быть «открыта» учащимися самостоятельно пу- тем наблюдения за моделью, которая отражает эту зависимость.

Модель можно изготовить из спиц (рис. 96). Одна спица АВ крепится неподвижно, другая спица А С закрепляется в точке А и может вра- щаться вокруг нее, занимая положения АС_Ь АС₂ и т.д. Эта модель хорошо иллюстрирует зави- симость между изменением угла а\ который образуется спицами АВ и АС и косинусом угла а (такую модель можно продемонстрировать и с помощью компьютера).

Следующий важный момент в изучении три- гонометрических функций - введение sin a, cos а и tg а, где 0° < а < 180°.

Рис. 96

б) Определение синуса, косинуса и тангенса любого угла от 0° до 180°

Мотивация расширения области определения тригонометрических функ- ций может быть осуществлена следующим образом. Учитель напоминает уча- щимся, что им уже известны некоторые зависимости между сторонами тре- угольника: 1) в любом треугольнике каждая сторона меньше суммы двух дру- I их сторон; 2) в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.

Возникает вопрос. Нельзя ли так же определённо, как и для прямоугольно- к) треугольника, выразить зависимость между сторонами любого треугольника? Га кая зависимость существует. Однако для ее выявления необходимо расширить понятие косинуса острого угла на любой угол от 0° до 180°.

В учебнике А. В. Погорелова это делается следующим образом. Берется окружность на плоскости ху с центром в точке О радиуса R (рис. 97). От поло- жительной полуоси х в верхнюю полуплоскость откладывается угол а.

Пусть х и у координаты точки А, тогда для

х . у у

острого угла се cosа = —, sma = —,tga = —.

R R х

Затем значения sin а, cos а я tg а определя- ются этими формулами для любого угла а. (Для tg а угол а *90°.)

При таком определении sin 90° = 1; cos 90° = 0; sin 180°= 0; cos 180° = -1; г&180° = 0.

Если считать, что совпадающие лучи образу- ют угол 0°, будем иметь:

sin 0° = 0; cos 0° = 1; tg 0° = 0.

253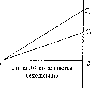

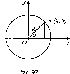
Необходимо акцентировать внимание учащихся на том, что при измене­нии а от 0° до 180° каждому значению а соответствует единственное значение cos а и единственное значение sin а; при изменении а от 0° до 90° (0° < а < 90°) и от 90° до 180° (90° < а <180°) каждому значению а соответствует единствен­ное значение tg а. Таким образом, косинус и синус являются функциями угла

а, где 0° < а < 180°, а тангенс - функцией угла а, где 0° < а < 90° и 90° < а <180°.

Функции sin a, cos а и tga называются тригонометрическими функ­циями. Введенное определение sin a, cos а и Наследует закрепить с помо­щью упражнений типа:

Упражнение. Вычислить cos 120°, sin 120° и tg 120°, используя опре­деления sin а, cos а и tg а.

После сообщения этих фактов доказывается теорема, что для любого угла а, 0°< а < 180°

sin (180° - а) - sina, cos (180°--а) = - cos а.

Для угла а*90°, /g(180°- a) = -tg а .

Необходимо подчеркнуть практическую значимость теоремы: она позво­ляет сводить вычисления sin а, cos а (0° < а < 180°) и tg а, а ф 90°, к вычисле­нию синуса, косинуса и тангенса острого угла.

После определения косинуса угла а (0°<а<180°) с учащимися обсуж­дается зависимость между сторонами треугольника, задаваемая теоремой коси­нусов. Следует обратить внимание учащихся на то, что теорема Пифагора явля­ется её частным случаем. В учебнике Л. С. Атанасяна и др. доказательство тео­ремы косинусов основано на координатном методе (В учебнике А. В. Погоре- лова на векторном методе).

Затем сообщается и доказывается теорема синусов. Теорема синусов эф­фективна тогда, когда заданы два угла и сторона треугольника, теорема косину­сов используется, если заданы две стороны и угол между ними. Далее выража­ется связь между стороной правильного треугольника и радиусом описанной (вписанной) окружности, площадью треугольника и произведением длин двух его сторон. Тригонометрические функции используются также при выводе формулы площади крута и формулы Герона.

В учебнике JI. С. Атанасяна и др. для 9 класса тригонометрическим функциям и соотношениям между сторонами и углами треугольника посвящена отдельная глава (см. Таблицу 1). В отличие от учебника А. В. Погорелова синус угла а (0° < а < 180°) вводится здесь как ордината у точки М перечения луча h, образующего с положительной полуосью абсцисс угол а, и единичной по­луокружности; косинус угла - абсцисса х точки М.

Определение синуса и косинуса угла а в учебнике являются генетическими определениями: вначале разъясняется происхождение точки М, а затем говорится, что «синусом угла а называется ордината у точки М, косинусом угла - абсцисса х точки М».

254