шпоры 13-16

14. Нелинейная регрессия. Линеаризируемые и нелинеаризируемые модели. эластичность

Линейная регрессия является частным, и не самым распространенным случаем регрессии.

Примером нелинейной регресии явл.: 1) 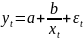- гипербола;2)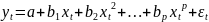 -полиномиальная;3) 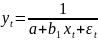- обратная;4)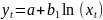 - полулогарифмическая; 5) – степенная; 6) 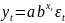– показательная; 7) – логическая.

Различают два класса нелинейных регрессий. 1. Регрессии нелинейные относительно объясняющих переменных (факторов), но линейные по оцениваемым параметрам; 2. Регрессии нелинейные по оцениваемым параметрам. Оценка неизвестных параметров нелинейных регрессий первого класса решаются без сложностей методом наименьших квадратов. Возможны и иные модели, нелинейные по фактору, но линейные по неизвестным параметрам.

Все случаи регрессий нелинейных по оцениваемым параметрам делятся на 2 типа: внутренне линейные и внутренне нелинейные модели. Внутренне линейная модель с помощью математических преобразований может быть сведена к линейному виду. Если же модель внутренне нелинейна, то она не может быть сведена к линейной модели. Особый интерес среди нелинейных функций регрессии представляет степенная функция . Параметр b в ней имеет четкое экономическое истолкование — коэффициент эластичности. Величина параметра b показывает на сколько процентов в среднем изменяется результат при изменении фактора на 1%.

В общем случае, коэффициент эластичности может быть определен для любой функции регрессии 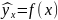формуле 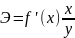. Только для степенной функции коэффициент эластичности — величина постоянная. Для других функций коэффициент эластичности зависит от значений фактора х. Поэтому обычно рассчитывают средний показатель эластичности. Для линейной регрессии он может быть выражен как .

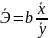13. Интервалы прогноза по линейному уравнению регрессии

Основное назначение уравнения регрессии — прогноз возможных значений результата при заданном значении фактора. Этот прогноз осуществляется путем подстановки значения фактора Х = 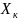в уравнение регрессии 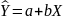. Но данный точечный прогноз не всегда реален. Он должен дополняться расчетом стандартной ошибки 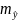и соответственно интервальной оценкой прогноза значения результата Y*. Т.е. Y*∈[ − ; + ]. Получим данную оценку. Для линейной регрессии . Подставим

это выражение в уравнение . =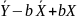 = 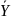+ b(X − 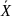) . Отсюда следует, что стандартная ошибка зависит от ошибки и ошибки коэффициента b, т.е.

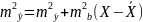Из математической статистики известно, что 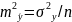. Возьмем в качестве оценки 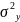остаточную дисперсию на одну степень свободы 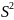, получим 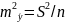; ; 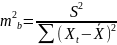Считая, что прогнозное значение равно получим следующую формулу расчета квадрата стандартной ошибки предсказания 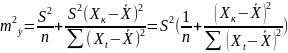. Откуда

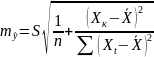
Величина стандартной ошибки предсказания зависит от , достигает минимума при = X и возрастает по мере того, как «удаляется» от X в любом направлении. Для прогнози-руемого значения 95%-ные доверительные интервалы при

заданном определяются выражением 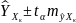. На графике доверительные границы для 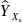представляют собой гиперболы, расположенные по обе стороны от линии регрессии. Фактические значения Y варьируют около среднего значения на величину случайной ошибки ε, дисперсия которой оценивается как остаточная дисперсия на одну степень свободы . Поэтому ошибка предсказываемого индивидуального значения Y должна включать не только стандартную ошибку 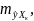но и случайную ошибку S. Средняя ошибка прогнозируемого индивидуального значения у составит:

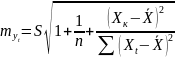
15. Корреляция для нелинейной регрессии. Средняя ошибка аппроксимации Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции R: 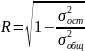, где 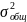— общая дисперсия результативного признака у; — остаточная дисперсия. Т.к. 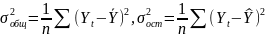, то индекс корреляции можно выразить как: 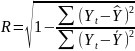. Величина данного показателя находится в границах: 0 < R < 1, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. Если нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадет с индексом корреляции.

Иначе обстоит дело, когда преобразования уравнения в линейную форму связаны с зависимой переменной. В этом случае линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи и численно не совпадает с индексом корреляции. Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину для нелинейных связей называют индексом детерминации. Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера: 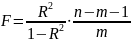, где — индекс детерминации; n — число наблюдений; m — число параметров при переменных х.

Величина т характеризует число степеней свободы для факторной суммы квадратов, а (n – m – 1) — число степеней свободы для остаточной суммы квадратов. Индекс детерминации можно сравнивать с коэффициентом детерминации 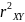для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии тем величина коэффициента детерминации меньше индекса детерминации . Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина ( – ) не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия, вычисленных по одним и тем же исходным данным, через t-критерий Стьюдента: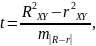 где — ошибка разности, определяемая по формуле: 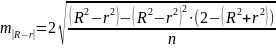Если 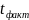> 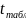то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически если величина t < 2 , то различия между

и 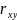несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т. е. 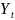и 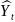. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака ( 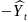) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения ( ) несравнимы между собой, исключая величину, равную нулю. Поскольку ( ) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю. Отклонения ( ) можно рассматривать как абсолютную ошибку аппроксимации, а 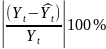как относительную ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:

16. Множественная регрессия. Спецификация модели. Отбор факторов

Парная регрессия используется в случае, когда на результативный признак оказывает существенное влияние один фактор, а все прочие факторы являются несущественными и входят в ошибку измерения. Если нельзя исключить несколько факторов как существенных, то получаем случай множественной регрессии.

Общий вид: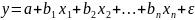

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Она включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.

Включение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего, с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, когда 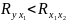для зависимости у = а + 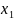+ +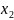ε может привести к нежелательным последствиям — система уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Включаемые во множественную регрессию факторы Должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других не учтенных в модели факторов оценивается как 1 – с соответствующей остаточной дисперсией . При дополнительном включении в регрессию р + 1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться: 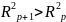и 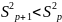. Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор 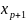не улучшает модель

и практически является лишним фактором.

Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента. Хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй — на основе матрицы показателей корреляции определяют t-

статистики для параметров регрессии. Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменных явно коллинеарны, т. е. находятся между собой в линейной зависимости, если ≥ 0,7