Составление уравнений вертикальных колебаний моделей с одной степенью свободы при кинематическом возмущении.

Число степеней свободы - это число дополнительных связей, которые необходимо наложить на систему, чтобы сделать равными нулю все возможные перемеще­ния.

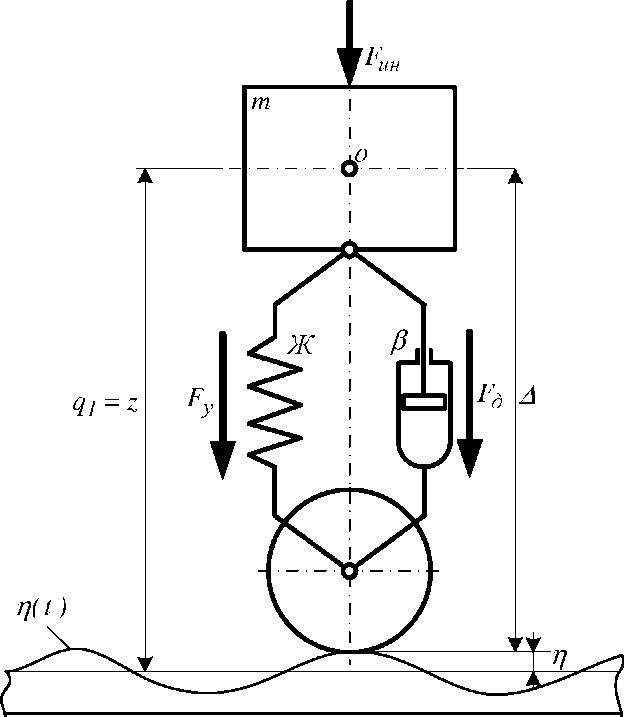
Путь считается абсолютно жестким. Данная модель позволя­ет оценить особенности динамиче­ских свойств, определяемых ее структурой и характером возмуще­ния, а также данная модель в первом приближении соответствует вагону с одноступенчатым рессорным подвешиванием.

Масса m на расчетной схеме соответствует сумме масс кузова и тележек, а жесткость Ж и коэффициент затухания β являются эквивалентными характеристиками рессорного подвешивания.

При движении системы, кинематическое возмущение вызывает вертикальные колебания надрессорного строения, которые характеризуются одной обобщенной координатой q₁ = z (подпрыгивание).

В системе действуют силы:

• сила инерции F_ин =

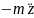
• упругая сила Fy = ,

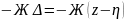• диссипативная сила F∂ =

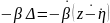
Используя принцип Даламбера, уравнение колебаний рассматриваемой динамической модели записывается

F_ин + Fy + F∂ = 0.

с учетом формул

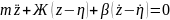
Преобразуем полученное уравнение, перенеся в правую часть члены с возмущающим воздействием

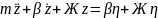
Полученное уравнение представляет собой уравнение вертикальных колебаний модели (колебаний подпрыгивания) с одной степенью свободы, левая часть которого это собственные колебания, а правая - вынужденные (т.к. правая часть - сила от кинематического возмущения).

Решение уравнения колебаний позволит получить значения вертикальных перемещений z, скоростей и ускорений 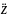массы m и приближенно оценить динамические свойства модели.

Уравнение колебаний модели с одной степенью свободы при силовом возмущении.

Вертикальные колебания массы m могут возникать не только в результате движения колеса по неровностям рельс, но и в том случае если на указанную массу действует внешняя возмущающая сила.

В данной схеме кинематическое возмущение отсутствует, а закон изменения силового возмущения F_B во времени задан.

Уравнение вертикальных колебаний динамической модели имеет вид:

F_ин + F_у +F_∂ + F_B = 0

В связи с тем, что кинематическое возмущение отсутствует 𝜂 = 0, то упругая и диссипативная силы соответственно определяются:

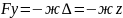
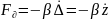
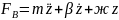
Решение данного уравнения позволяет решать задачи виброзащиты силового оборудования от вращения несбалансированных частей.

Уравнение колебаний модели плоской двухосной тележки.

Используя такую модель можно получить подробную информацию динамических свойств вагона. Появляется возможность учесть, кроме подпрыгивания ещё и колебания галопирования, а также неодновременность задания (запаздывание) возмущения по две колесных пары.

Рисунок.

В модели масса m (тележка) совершает колебания (подпрыгивания) z и галопирование φ_у. Причиной колебаний являются возмущения 𝜂₁(t) и 𝜂₂(t) передаваемые через первую и вторую колесные пары. При движении экипажа с поступательной скоростью υ неровность 𝜂₂ повторяет неровность 𝜂₁ через некоторое время τ, называемым транспортным запаздыванием. Это время определяется скоростью движения υ и расстоянием между осями колесных пар 2am и рассчитывается по формуле:

τ=2am / υ

Выражение для неровностей под первой и второй колесными парами запишется в следующем виде:

𝜂₁(t) = 𝜂(t)

𝜂₂(t) = 𝜂 (1 – τ)

𝜂(t) – единичное возмущение входного воздействия.

Уравнение колебаний подпрыгивания примет следующий вид:

F_ин + F_у1 +F_∂1 + F_у2 + F_∂2 = 0

Перемещение в точках 1 и 2 складываются из колебаний подпрыгивания z и вертикальных составляющих угловых колебаний галопирования φ_у.

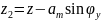
С учетом малости угла φ_у 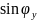= 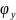, получаем:

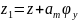
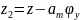
Силы входящие в уравнение вертикальных колебаний определяются:

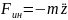
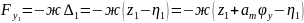
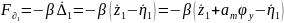
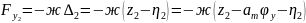
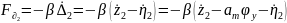
Подставляя в общее уравнение, получим:

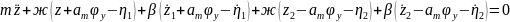
Для вывода уравнения колебания галопирования составим уравнение моментов, которое будет выглядеть следующим образом:

M_ин + M_у1 +M_∂1 + M_у2 + M_∂2 = 0

M_ин = - I_y φ_у

где I_y – момент инерции.

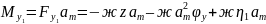
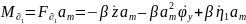
Окончательное уравнение:

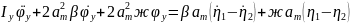
Таким образом колебания рассматриваемой модели описываются двумя уравнениями, эти колебания между собой не связаны. Данная модель позволяет получить различные значения ускорений и перемещений по длине и различные показатели динамики в комплектах рессорного подвешивания.

Гасители колебаний.

Распространенными гасителями колебаний являются фрикционные, они могут создавать постоянную или переменную величину сил трения. У фрикционных гасителей сила трения направлена в сторону обратную скорости перемещения, таким образом, если сила трения F_тр , то сопротивление гасителя

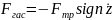
- величина скорости перемещения.

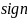- обозначение знака .

Если скорость положительна, т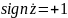о и наоборот, если скорость отрицательна, то 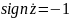. Постоянная величина сопротивления при движении в одном направлении F_B, в разных – F_н.

Наиболее распространенные гасители с переменными силами сопротивления, у которых сила трения пропорциональна перемещениям

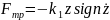
- величина перемещения от положения равновесия колебательной системы,

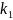- коэффициент пропорциональности, зависящий от конструкции гасителя,

,

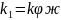φ- коэффициент относительного трения фрикционных гасителей колебаний,

ж – жесткость упругого элемента,

k – коэффициент пропорциональности, показывающий какую долю усилия при сжатии рессоры на единицу перемещения гаситель преобразует нормальное давление между трущимися элементами.

Гидравлические гасители – у этих гасителей сопротивление пропорционально скорости перемещения элементов гасителя.

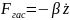
Существуют гидравлические гасители, у которых сопротивление пропорционально квадрату скорости перемещения

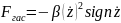
Выбор типа гасителя определяется характеристиками колебательных систем.