леэ19. Обработка экспериментальных данных.

На практике часто возникает следующая задача. Известно экспериментальная таблица где n – количество проведенных экспериментов:

xi	x1	x2	…	xn
yi	y1	y2	…	yn

На основе этой таблице необходимо получить зависимость между величинами x и y . В общем случае в эту зависимость могут входить некоторые параметры, поэтому такая зависимость в более общих случаях имеет вид .

Уравнение (1) или (2) называют уравнением связи или еще эмпирическим уравнением. Решение этой задачи проводится в два этапа: 1) Определение вида ф-ии . 2) нахождение параметров

Определение вида фун-ии .

Вид фун-ии иногда можно определить из физических или других соображениях. Например, если рассматривать равноускоренное или равнозамедленное движение то пройденный путь S и t связаны квадратичной фун-ией: . Если теоретическая предпосылка отсутствует то для определения вида функции можно использовать графический способо, который заключается в следующем: Берется система координат связанная с хар-ом решаемой задачей. На эту систему наносят экспериментальные точки.

Затем проводят кривую которая наилучшим образом соответствует этим экспериментальным точкам. Сравнивая эту кривую с графиками известных фун-ий, определяют вид функции . На практике отдаю предпочтения наиболее простым зависимостям. Рассмотрим некоторые из них: 1) линейная зависимость , Введем в рассмотрение k: (4), где . Если коэффициент k_i=const приближенно равны между собой, то использование линейной зависимости яв-ся обоснованным.

Если при этом , то достаточно проверить постоянство .

2) квадратурная зависимость:

Введем в рассмотрение l_i: 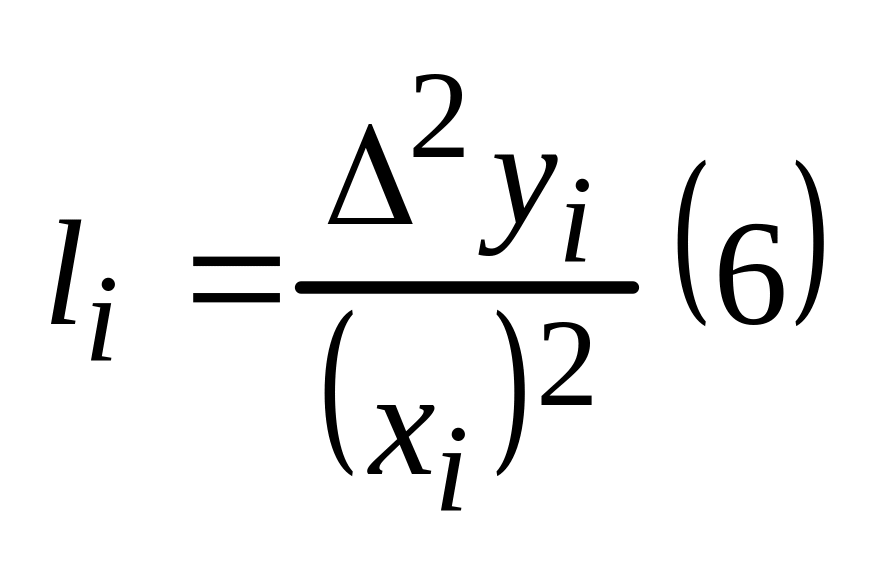, где

Если l_i≈const, то использование квадратичной зависимости является оправданием.

l_i – дискретный аналог II производной.

Если при этом , то достаточно проверить

Замечание1. Иногда к простым зависимостям удается привести другие функциональные связи, н-р, если имеется зависимость , то путем логарифмирования ,

Замечание2. Если на всем отрезке [a;b] трудно определить зависимость, подходящего для описания экспериментальных данных, то можно поступить следующим образом, отрезок [a;b] разделить на несколько частей и в каждой из них использовать некоторую простую зависимость . А в точках стыка можно оставить условие, обеспечивающее непрерывность всей функции в целом.

20. Метод наименьших квадратов(мнк)

Математически наиболее обоснованным и эффективным яв-ся метод МНК. Допустим что первая часть задачи решается, т.е. определен вид ур-я связи: , где a₁,…,a_m –неизвестные параметры. Введем в рассмотрение величину - погрешность i-го эксперимента .

Вводится далее среднеинтегральная хар-ка : -интегральная сумма

здесь - ф-я от неизвестных параметров.

Идея МНК.

Неизвестные параметры a₁,…,a_m определяют так, чтобы величина была минимальной. Таким образом задача сводится к минимизации функциональных переменных.

Такая задача решается с помощью частных производных, находят все частные производные первого порядка и приравниваются к нулю

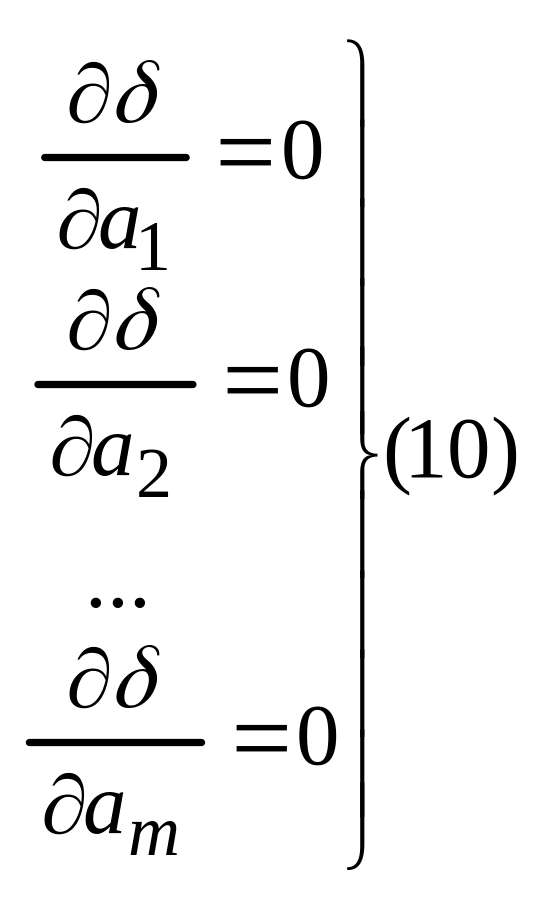Систему (10) называют нормальной системой МНК. Выведем системы для нормального случая.

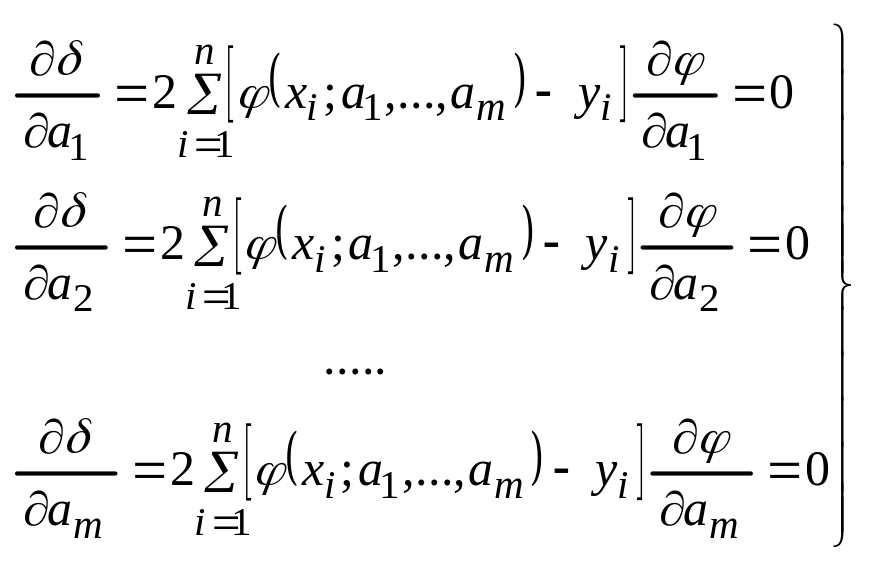
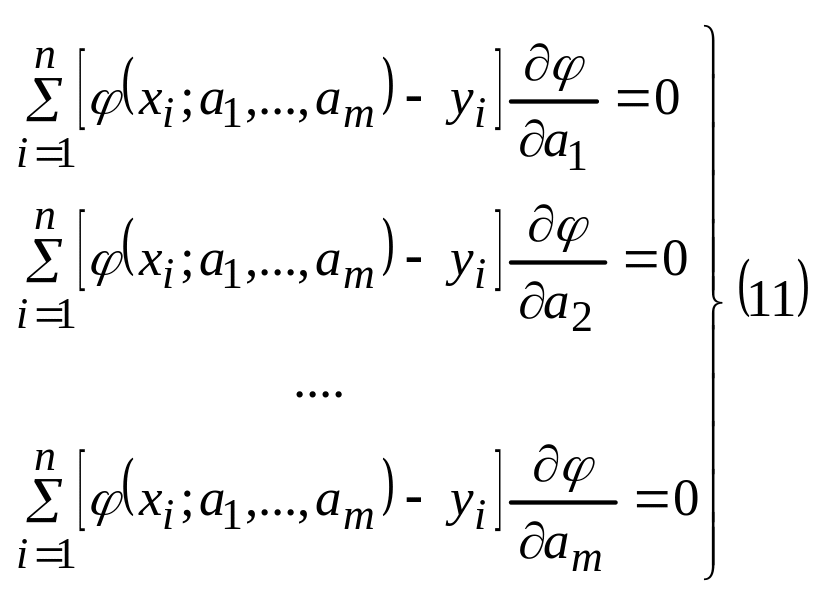
Решая эту систему ур-ий определяют значение неизвестных коэффициентов и подставляют эти значения в фун-ю (7). Полученную аппроксимирующую фун-ю можно использовать для приближенного вычисления значения величины y для

21. Линейное приближение квадратов по МНК.

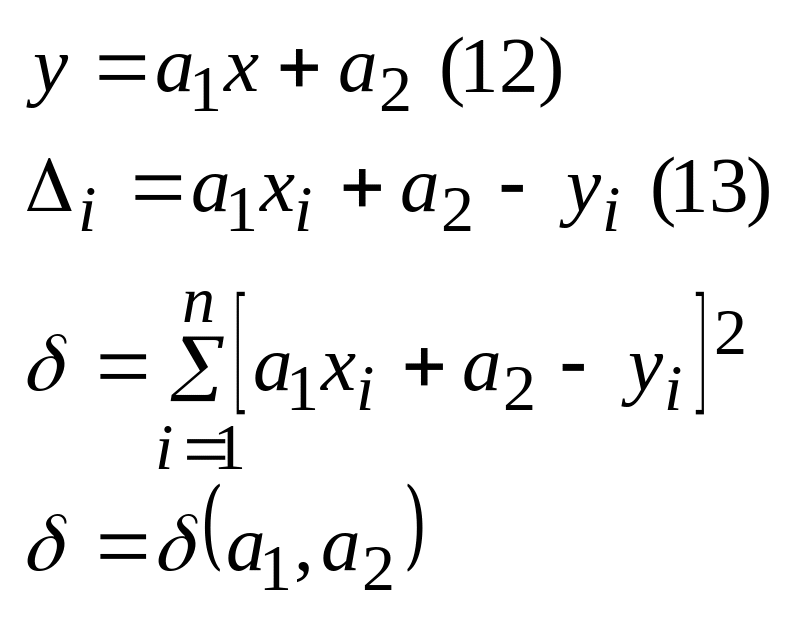
Построим систему для такого вида уравнения связи:

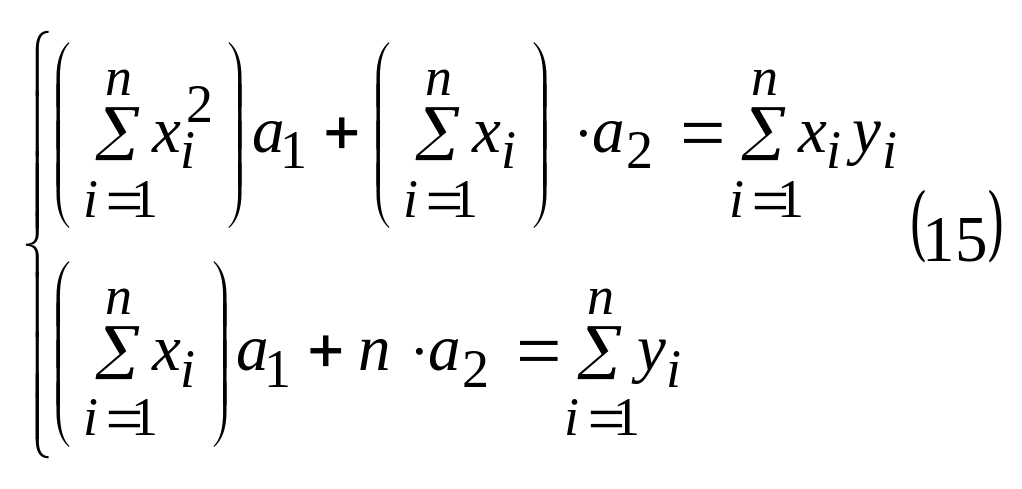
22. Квадратичное приближение квадратов по МНК.

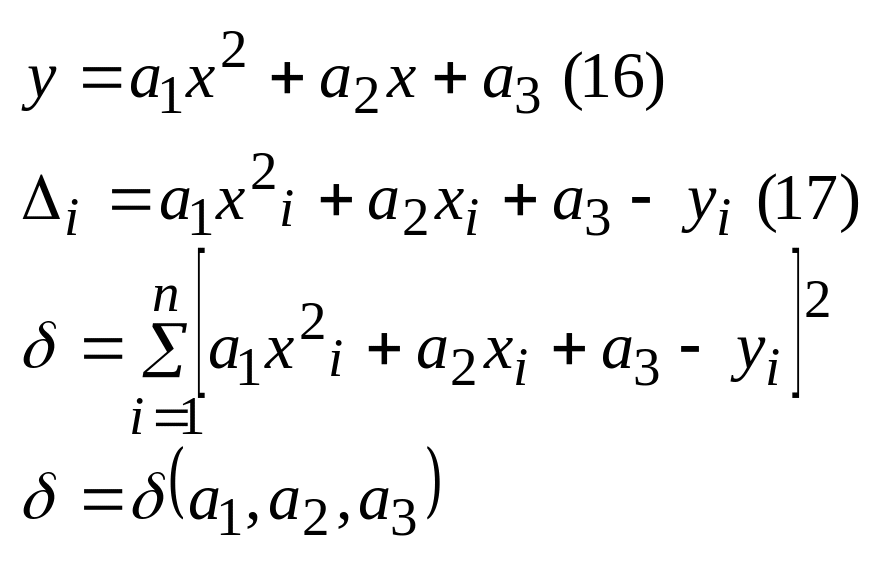
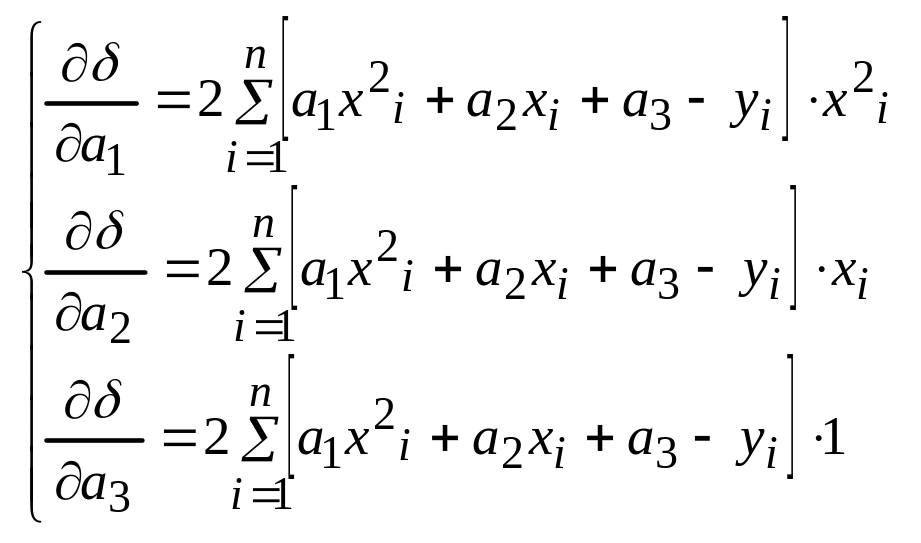
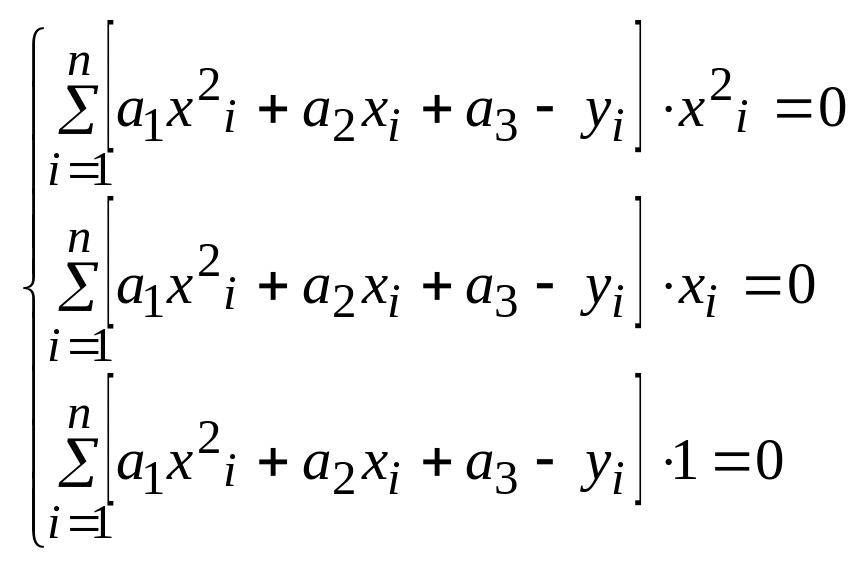
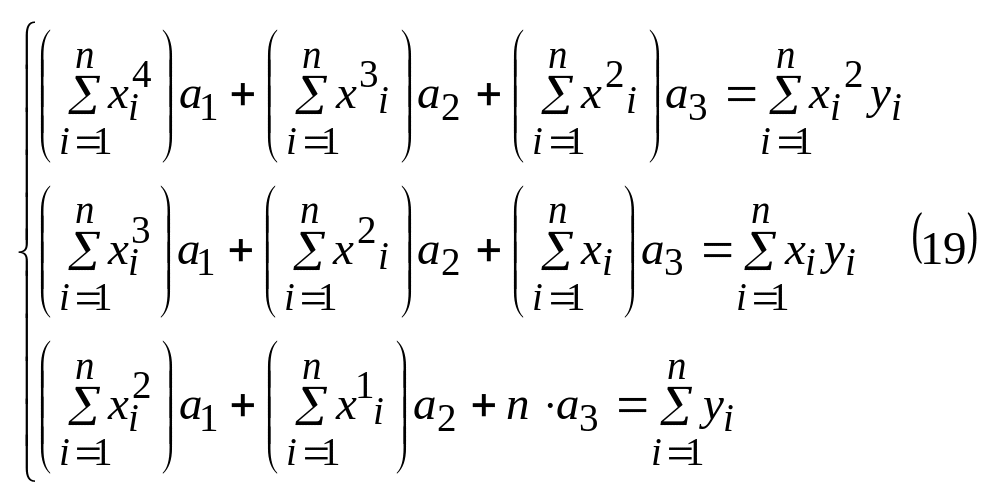
Свойства 1. Матрицы систем (15),(19) является симметричным,если

23. Полиномиальное приближение по МНК.

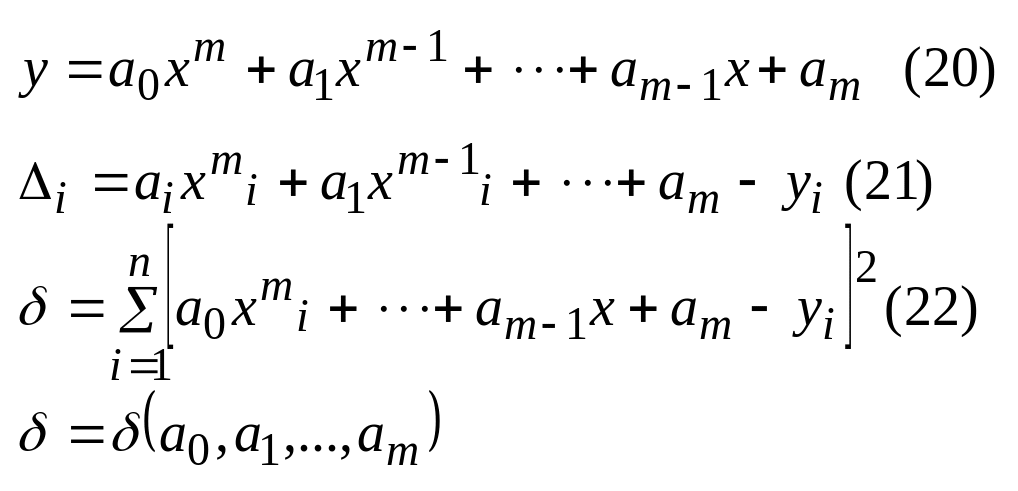
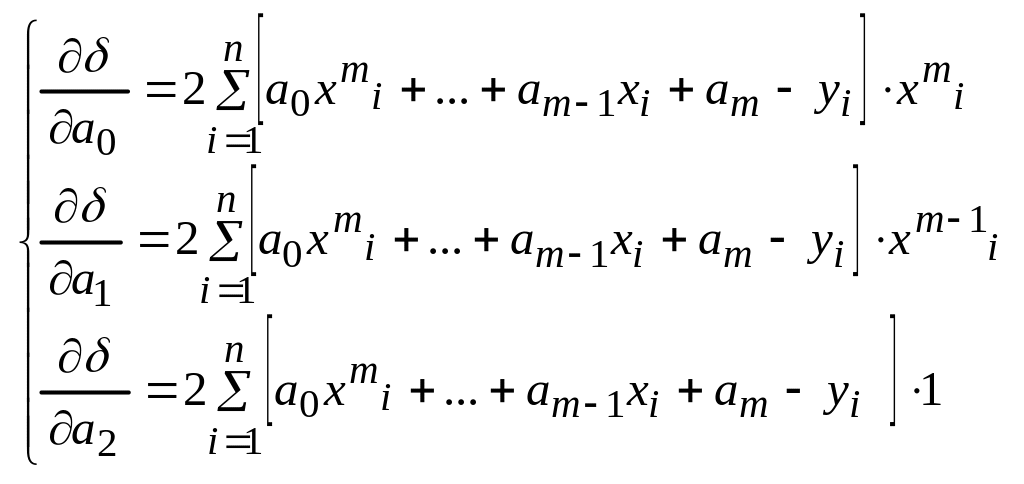
Свойство 2

Матрица системы (23) является симметричной матрицей.

24. Численное дифференцирование. Формулы численного дифференцирования основанные на применении ИПН.

На практике часто возникает следующая задача: необходимо найти производные указанных порядков от таблично заданной функции.

Постановка задачи

На [a;b] дано разбиение

,

xi	x0	x1	…	xn
yi	y0	y1	…	yn

Формулы численного дифференцирования основанные на применении ИПН.

Д ругим способом решения задачи численного дифференцирования явл-ся использование интерполяционных полиномов. Основная идея этого подхода заключается в следующем. Сначала на основе известной информации фун-ию заменяют приближенно: - интерполяционный полином. Затем за производную от фун-ии приближенно принимают производную от полинома: . Если нужны производные более высоких порядков, то поступают аналогичным образом .

Примечание. Обратимся к геометрической иллюстрации основной задачи фун-ии интерполирования.

Пусть на нужны f’(x). Построим в точке x₁ касательную к полиному и фун-ии. Угловые коэффициенты касательных . На [a;b] возьмем систему равноудаленных точек

Нужно найти

Для решения задачи используем первый Интерполяционный полином Ньютона. Он имеет вид

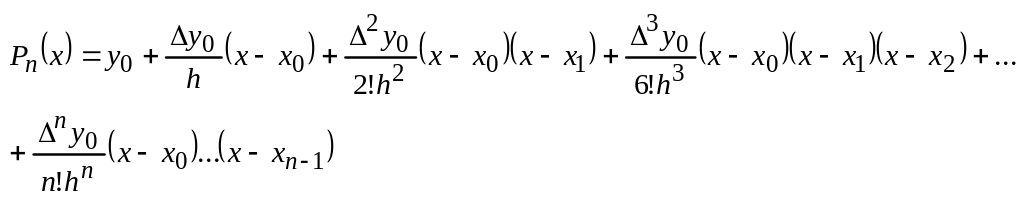(10)

Для удобства при дифференцировании перейдем к q

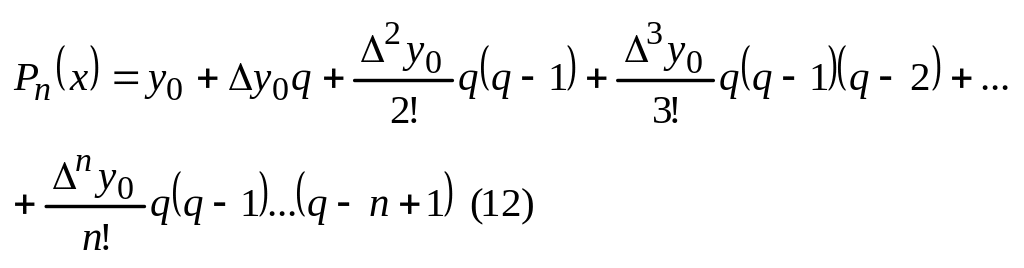
_; Из (1) ;

Для удобства при дифференцировании перемножим биномы в (12)

Формула для вычисления производной 1-го порядка:

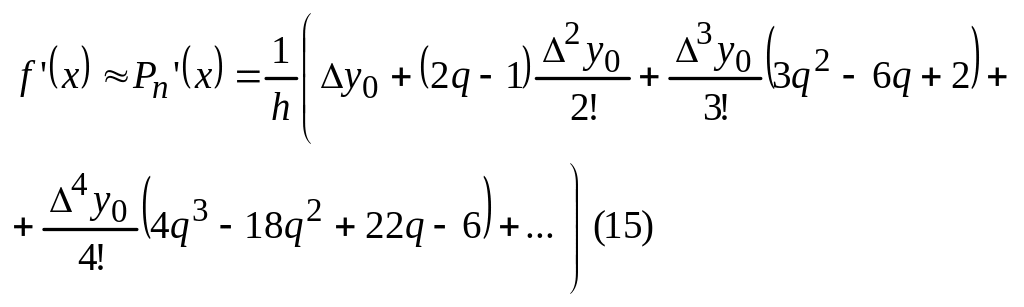
Формула вычисления производной II го порядка:

Если нужны формулы для производных более высоких порядков, дифференцирование продолжается аналогичным образов.