32. Численное решение задачи Коши для оду 1 порядка методом Рунге-Кутта.

Существует семейство методов Рунге-Кутта, расм-м вариант метода, который наиболее часто применяется на практике.

Отрезок [a;b] разобьем на n-равных частей точками x_i.

Выделим произвольный элементарный учаcток [x_i,x_i+1] и все рассуждения проведем относительно этого участка.

Значение искомого решения

-средняя взвешенная сумма поправочных коэффициентов

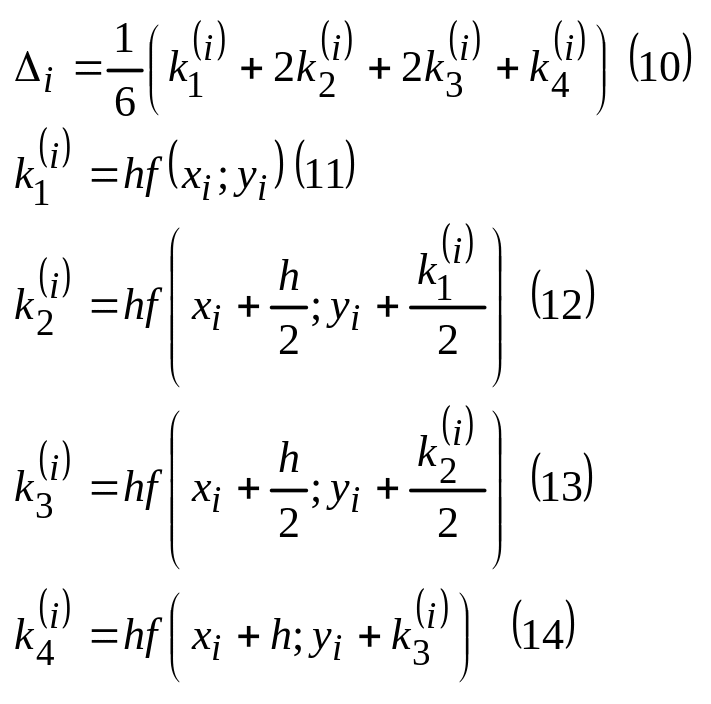, где

На всем отрезке [a;b] погрешность составляет величину O(h⁴), поэтому можно сделать вывод, что метод Рунге – Кутта дает практически точное решение задачи Коши (диф. ур-я). Метод часто применяется для решения практических задач и реализован в виде программ на разных языках программирования.

33. Система оду I порядка. Метод Эйлера.

На практике в основном приходится решать системы из нескольких диф. ур-ий, поэтому рассмотрим случай n=2

Обозначим y₁=y

Начальное условие

Метод Эйлера.

Отрезок [a;b] разобьем на n-равных частей точками x_i и выделим произвольный участок [x_i;x_i+1]

34. Система оду I порядка. Метод Рунге-Кутта.

Отрезок разбивается на n – равных частей точек x_i взвешенные суммы 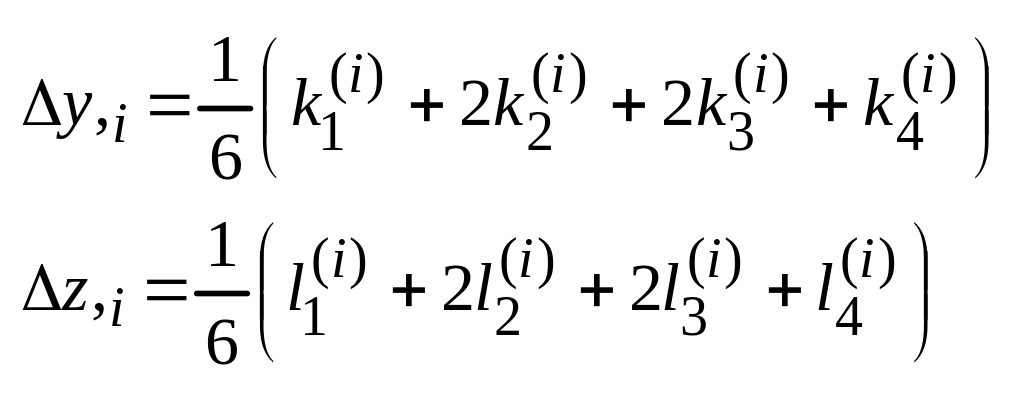(19)

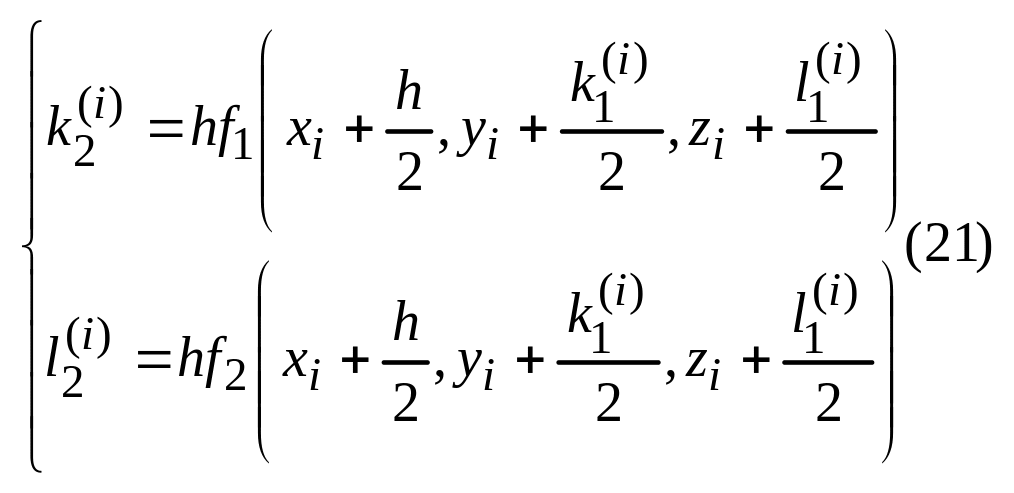
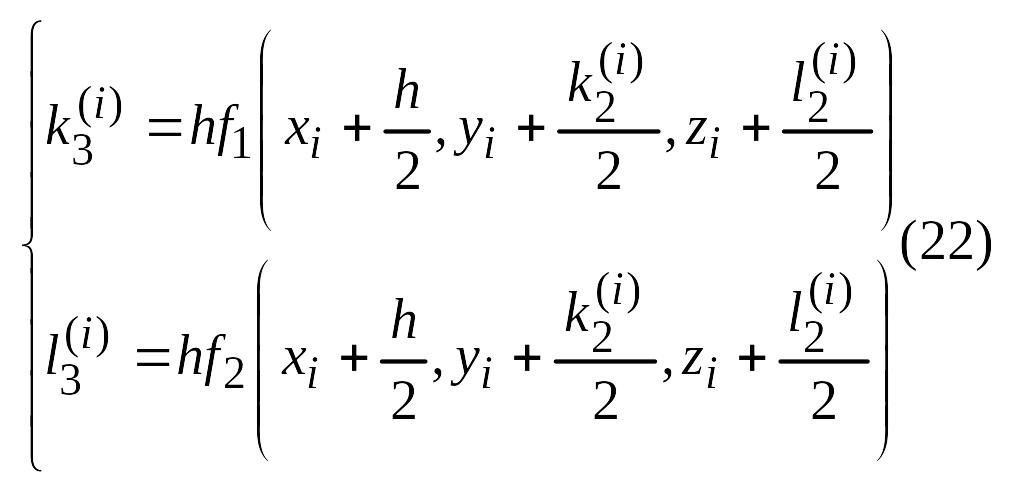
В этой серии формул

Замечание. Геометрический смысл коэффициента k₂(k₁,k₂,k₃,k₄), если взять для одного диф. ур.

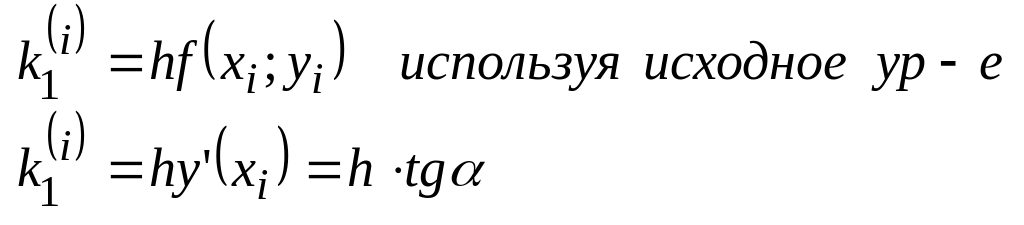
y’(x) – угловой коэффициент к кривой в точке с абсциссой x_i.

Т .е. поправочные коэффициенты пропорциональны к угловым коэффициентам.

Если взять производную участка [x_i;x_i+1]

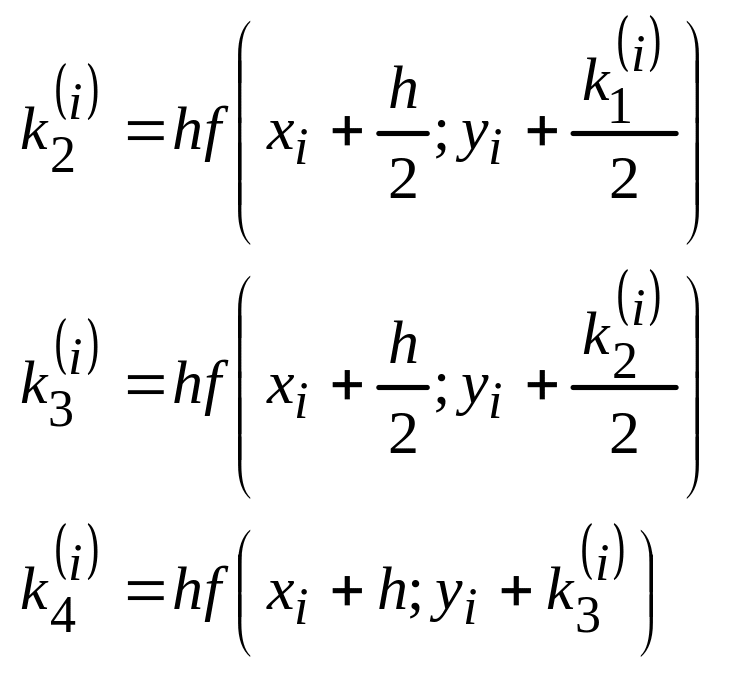
35. Конечно-разностный метод решения дифференциальных ур-ий I порядка. Построение конечно-разностной схемы.

1. Способы аппроксимации производных.

Опр. Сеткой называется множество угловых точек расположенных на некотором множестве определенным образом. В зависимости от геометрии задачи (от размерности) сетки могут быть одномерными, двухмерными или многомерными. Если в определенном направлении шаг постоянен, то в этом направлении сетка наз-ся равномерной. Пусть на отрезке [a;b] дана система равноудаленных точек.

Пусть значение функции в этих точках известны

xi	x0	x1	…	xn
yi	y0	y1	…	yn

Для аппроксимации производной первого порядка на практике часто используются следующие формулы

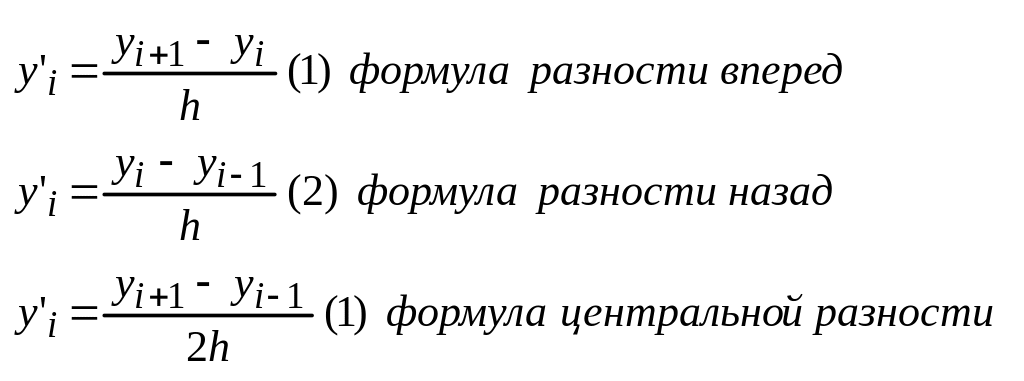
Эти формулы легко выводятся с использованием разложения функции в ряды Тейлора.

- разложение функции в окрестности точки x.

Выведем (1), для этого используем (4), в нем отбросим все слагаемые, содержащие h²,h³ и в более высоких степенях.

Говорят что , если существует константа C, такая .

Полученное уравнение решим относительно y’(x)

Перейдем к индексному обозначению,

сравним с (1)

Сравнивая формулы (1) и (9) заключаем, что формула (1) имеет погрешность O(h). Для вывода формулы (2) используем разложение (5). В этом разложение выбросим все слагаемые, содержащие h²,h³ и т.д.

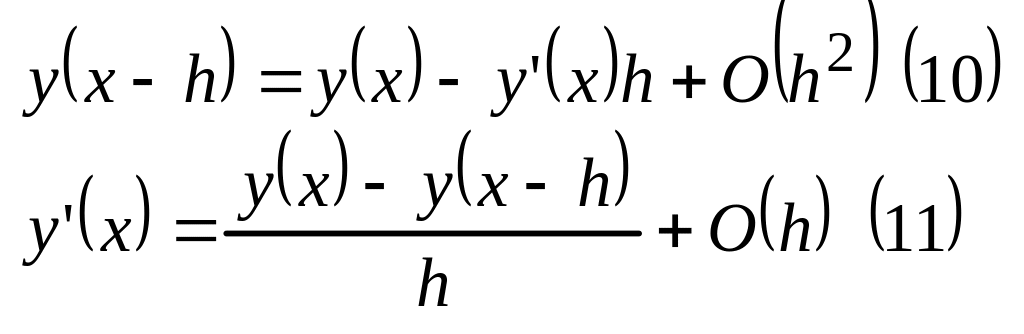
Переходя к индексному обозначению поучим

Сравнивая (2) и (12) погрешность замены производной пропорциональна………?

Для вывода формулы (3) одновременно используем разложения (4), (5).

В правой части (13) отбросим все слагаемые, содержащие h³ и в более высоких степенях.

Переходя к индексному обозначению получим

Сравнивая формулы (3) и (16) заключаем, что погрешность формулы (3) O(h²). Из этих 3х формул, формула (3) явл-ся более точной однако только на основе этого нельзя делать вывод о том, что получаемое решение будет более точным. В ряде случаев это более точная формула приводит к расходящемуся решению. В тоже время формула (2) дает сходящиеся решение при численном решение ряда ур-ий. С помощью разложения (4), (5) можно выводить также формулы для аппроксимации производных второго и более порядка. Выведем одну формул для аппроксимации производной второго порядка.

(4)+(5)

В этом разложении отбросим все слагаемые, содержащие h⁴ и в более высоких степенях, отбрасывая получим.

Переходя к индексному обозначению получим

На основе этого можно записать формулу (21) погрешность которой составляет O(h²)

Формулы для аппроксимации производной можно также выводить, используя методы численного дифференцирования.