25. Численное дифференцирование. Метод неопределенных коэффициентов.

На практике часто возникает следующая задача: необходимо найти производные указанных порядков от таблично заданной функции.

Постановка задачи

На [a;b] дано разбиение

,

xi	x0	x1	…	xn
yi	y0	y1	…	yn

Метод неопределенных коэффициентов.

xi	x0	x1	…	xn
yi	y0	y1	…	yn

Решение задачи ищут в виде:

, где c_i -? (1)

Здесь k- порядок производной

Предполагается, что равенство (1) вып-ся для каждой из следующих ф-ий

Фун-ии семейства (2) последовательно подставляются в равенство (1). В результате получается система уравнений относительно неизвестных коэффициентов c_i.

Решая полученную систему Ур-ий определяют значеня коэффициентов и подставляют в (1).

26. Формула численного дифференцирования, основанные на применении интерполяционных формула Лагранжа.

Полином Лагранжа имеет вид:

Узловые точки берутся равноудаленными, т.е

(18)

Где R(x) – остаточная погрешность относительно R(x). Если ф-я f(x) n-раз непрерывна дифференцируема, а n+1 – производная ограничена, то имеет место:

, где , где C- некоторая средняя точка между [a;b] ,

На практике заменяют

Точная замена дает

Рассмотрим частный случай при n=2

Преобразуем (21) с учетом , что h=const

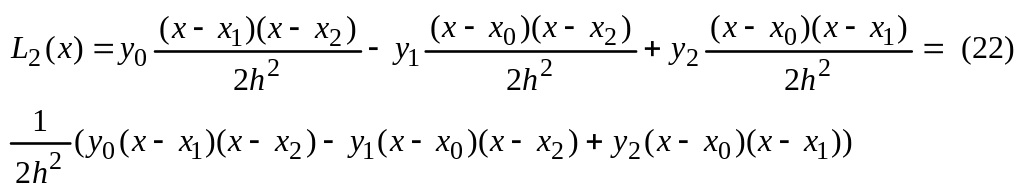
Если

Если

Выражение для R(x)

Производные в точки

Погрешность этой формулы

27. Численное интегрирование. Метод прямоугольников.

Ставится задача вычисления определения, интегралов:

Определение интеграла можно вычислить, по формуле Ньютона-Лейбница,

,

Однако на практике часто возникают следующие трудности:

1) F(x) первообразная не существует в классе элементарных фун-ий, интеграл не берется.

2) F(x) существует и яв-ся слишком сложной фун-ией и вычисление ее значений вызывает большие трудности.

3) Подынтегральная ф-ия задана лишь таблично, в этом случае теряет смысл вообще само понятие первообразной.

В таких случаях для вычисления определенных интегралов используют методы приближенного вычисления или методы численного интегрирования.

Вычисления однократного интеграла наз-ся механической квадратурой, а соответствующие формулы наз-ют квадратурами. Рассмотрим простейшие квадратурные ф-лы и их обобщения для вычисления.

Метод прямоугольников.

Вычислим определенный интеграл

Пусть положительна и непрерывна

Геометрический смысл интеграла – площадь криволинейной трапеции, ограниченной сверху f(x), слева и справа прямыми x=a, x=b и снизу осью абсцисс.

Отрезок [a;b] разобьем на n-равных частей точками x_i.

, проведем прямые x=x_i. Тем самым мы интеграл разбили на сумму интегралов 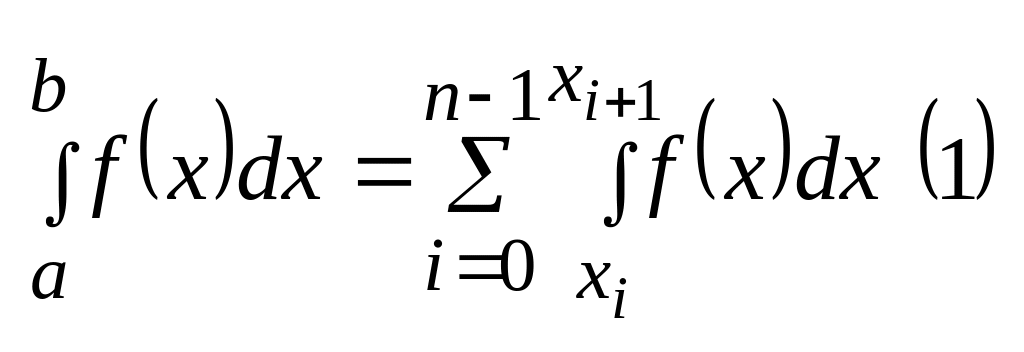, 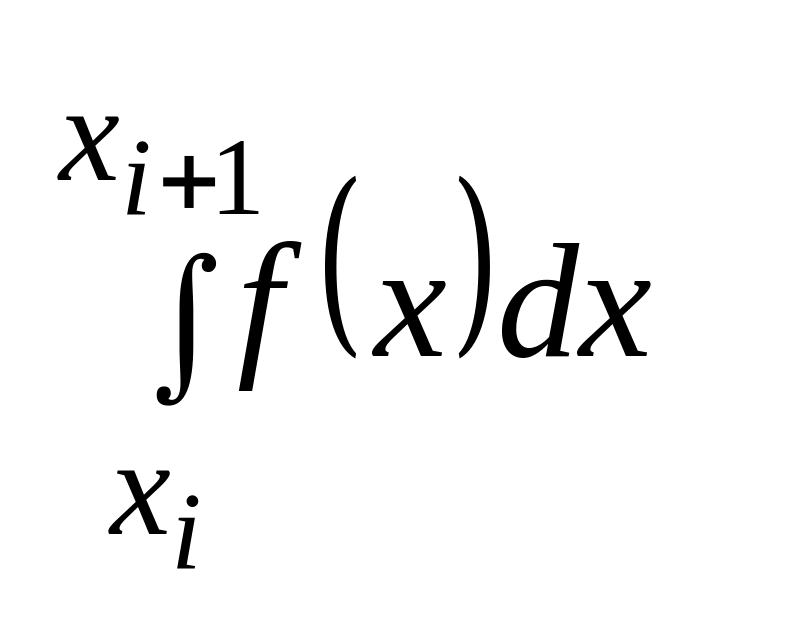- площадь произвольной полосы.

В методе прямоугольников площадь кажой такой полосы приближенно заменяется площадью прямоугольника.

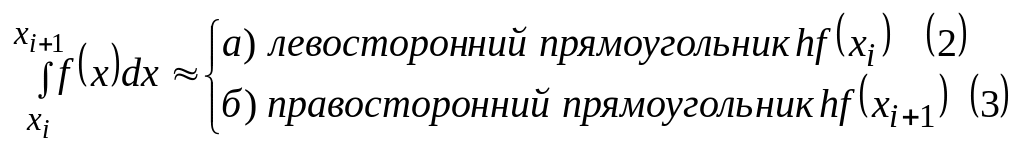
Это малые формулы левосторонних и правосторонних прямоугольников соответственно. Каждое слагаемое в формуле (1) заменим приближенно формулой (2) или формулой (3).

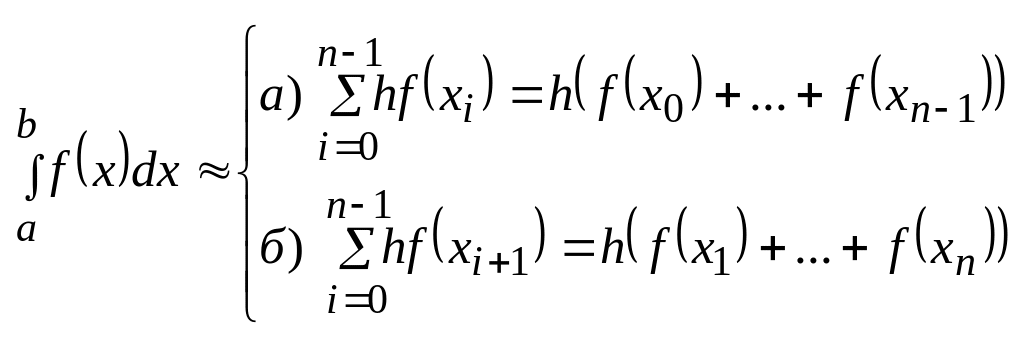, Таким образом

Это большие формулы левосторон. и правостороннего прямоугольников соответственно.

Введем в рассмотрение величину

Погрешность квадратичной формулы – разность между точным значением интеграла и значением полученные по формуле прямоугольного приближения.

Теорема №1.

Если производная функции существует и ограничена на отрезке [a;b], то

Док-во.

Согласно формуле (6) R(f) – разность эту разность запишем следующим образом: интеграл заменим суммой интегралов 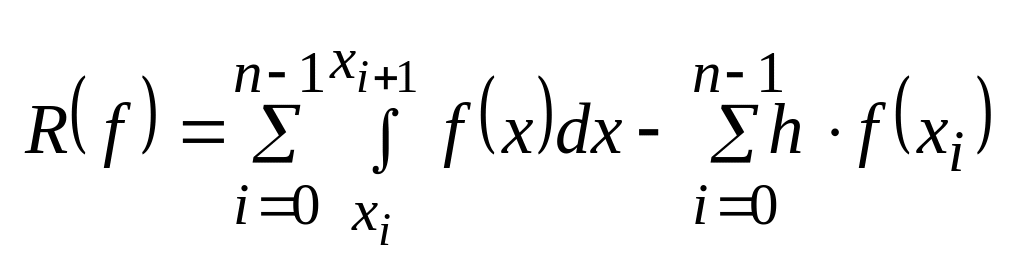(8)

Суммирую по одной и той же переменной в одних границах

,

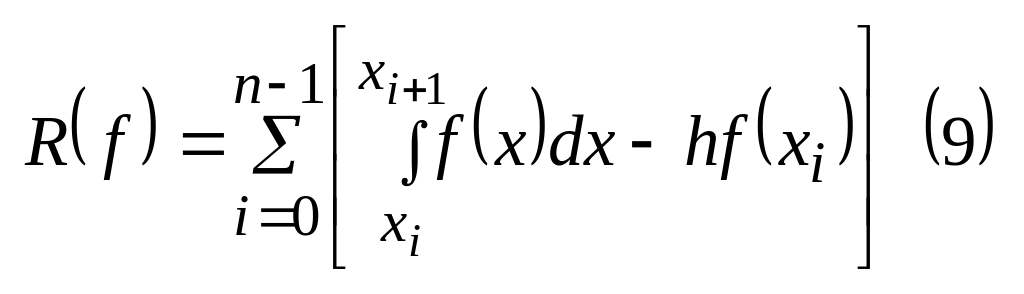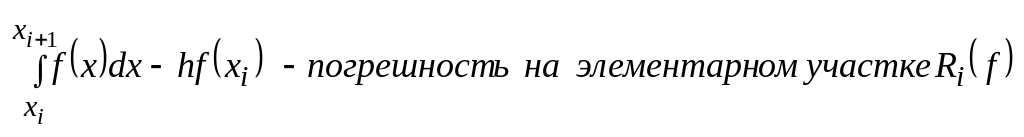
По условию теоремы функция дифференциально-непрерывная; применяя теорему о среднем

(=) (=), где C_i –некоторая промежуточная точка между x_i и x_i+1

(=) (=)

Применяем к этой разности теорему о конечном приращении Лагранжа согласно указанной теореме

(=) , где d_i – некоторая промежуточная точка между x_i и C_i

Таким образом

Обратим внимание на расположение точек

Отсюда . Модуль суммы не превышает сумму модулей , т.к. производная ограничена

ч.т.д.

Вывод:

Сравнение методов прямоугольников, трапеций и парабол на основе теоремы 1,2,3 можно сделать следующий простой вывод. Самым грубым яв-ся метод прямоугольников, а самый точный среди рассмотренных – метод парабол.

Квадратурная формула называется точной, если ее R(f)=0.