
- •20. Метод наименьших квадратов(мнк)
- •25. Численное дифференцирование. Метод неопределенных коэффициентов.
- •26. Формула численного дифференцирования, основанные на применении интерполяционных формула Лагранжа.
- •27. Численное интегрирование. Метод прямоугольников.
- •28. Численное интегрирование. Метод трапеций.
- •29. Численное интегрирование. Метод парабол.
- •30. Квадратурные формулы Ньютона-Котеса.
- •31. Задача Коши для обыкновенного дифференциального уравнения (оду) 1 порядка. Метод Эйлера.
- •32. Численное решение задачи Коши для оду 1 порядка методом Рунге-Кутта.
- •33. Система оду I порядка. Метод Эйлера.
- •34. Система оду I порядка. Метод Рунге-Кутта.
- •35. Конечно-разностный метод решения дифференциальных ур-ий I порядка. Построение конечно-разностной схемы.
- •36. Краевая задача для линейного обыкновенного дифференциального ур-я II порядка. Построение конечно- разностной схемы.
- •37. Первая краевая задача для уравнения теплопроводности. Явная конечно – разностная схема.
- •38. Первая краевая задача для уравнения теплопроводности. Неявная конечно-разностная схема.
- •41. Краевая задача для диф. Ур-ий частных производных
28. Численное интегрирование. Метод трапеций.
Ставится задача вычисления определения, интегралов:
Определение интеграла можно вычислить, по формуле Ньютона-Лейбница,
,
Однако на практике часто возникают следующие трудности:
1) F(x) первообразная не существует в классе элементарных фун-ий, интеграл не берется.
2) F(x) существует и яв-ся слишком сложной фун-ией и вычисление ее значений вызывает большие трудности.
3) Подынтегральная ф-ия задана лишь таблично, в этом случае теряет смысл вообще само понятие первообразной.
В таких случаях для вычисления определенных интегралов используют методы приближенного вычисления или методы численного интегрирования.
Вычисления однократного интеграла наз-ся механической квадратурой, а соответствующие формулы наз-ют квадратурами. Рассмотрим простейшие квадратурные ф-лы и их обобщения для вычисления.
Метод трапеций.
В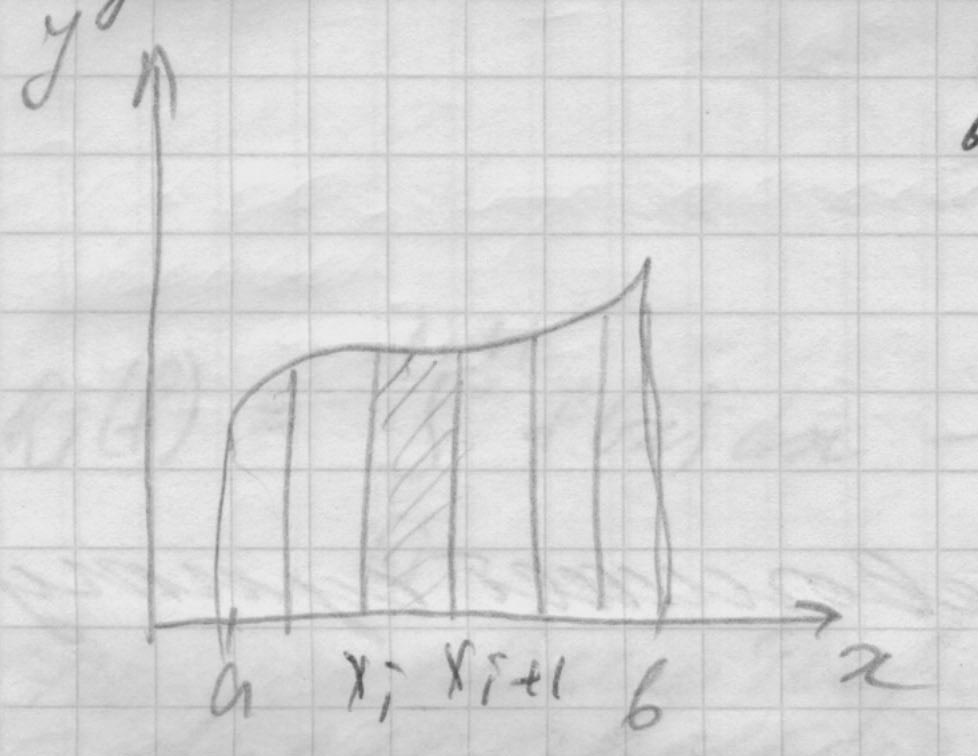 ычислим
определенный интеграл
ычислим
определенный интеграл
Пусть положительна и непрерывна
Отрезок [a;b] разобьем на n-равных частей точками xi.
,
проведем прямые x=xi.
Тем самым мы интеграл разбили на сумму
интегралов
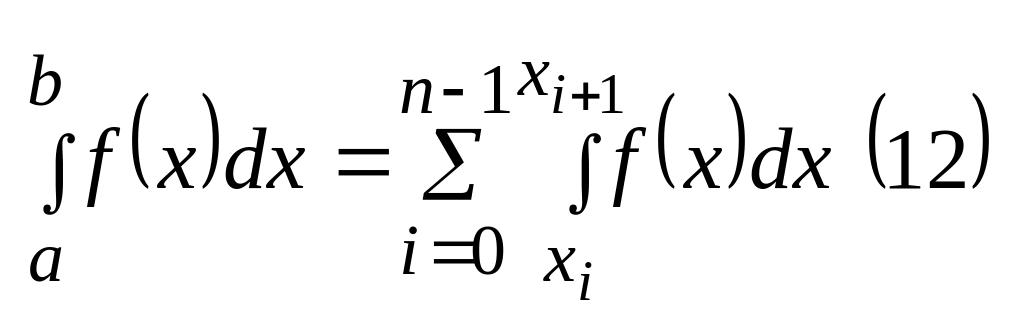 ,
,
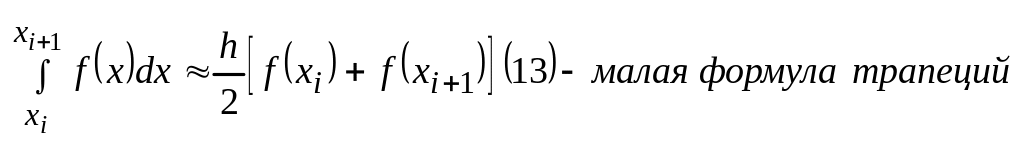
Площадь заштрихованной полоски заменяется приближенно площадью трапеции.
Заменяя каждое слагаемое в формуле (12) правой частью формулы (13)
![]() ,
распишем полученную сумму
,
распишем полученную сумму
![]() в полученной сумме
f(x0)
и f(xn)
встречается только
один раз.
в полученной сумме
f(x0)
и f(xn)
встречается только
один раз.
![]() .
Таким образом интеграл на всем отрезке
приближенно равен
.
Таким образом интеграл на всем отрезке
приближенно равен
![]() - большая формула трапеций.
- большая формула трапеций.
Введем в рассмотрение
погрешность квадратичной формулы
трапеции
![]() (15) разность между точками значений
интеграла и приближенное значение
интеграла и приближенное значение между
трапециями.
(15) разность между точками значений
интеграла и приближенное значение
интеграла и приближенное значение между
трапециями.
Теорема 2.
Если
![]() существует
и непрерывна на [a;b],
то
существует
и непрерывна на [a;b],
то
![]()
Док-во: почти аналогично предыдущему
Вывод:
Сравнение методов прямоугольников, трапеций и парабол на основе теоремы 1,2,3 можно сделать следующий простой вывод. Самым грубым яв-ся метод прямоугольников, а самый точный среди рассмотренных – метод парабол.
Квадратурная формула называется точной, если ее R(f)=0.
29. Численное интегрирование. Метод парабол.
Ставится задача вычисления определения, интегралов:
Определение интеграла можно вычислить, по формуле Ньютона-Лейбница,
,
Однако на практике часто возникают следующие трудности:
1) F(x) первообразная не существует в классе элементарных фун-ий, интеграл не берется.
2) F(x) существует и яв-ся слишком сложной фун-ией и вычисление ее значений вызывает большие трудности.
3) Подынтегральная ф-ия задана лишь таблично, в этом случае теряет смысл вообще само понятие первообразной.
В таких случаях для вычисления определенных интегралов используют методы приближенного вычисления или методы численного интегрирования.
Вычисления однократного интеграла наз-ся механической квадратурой, а соответствующие формулы наз-ют квадратурами. Рассмотрим простейшие квадратурные ф-лы и их обобщения для вычисления.
Метод парабол.
Отрезок [a;b] разобьем на четное число n=2k.
![]() ,
в качестве элементарного отрезка
,
в качестве элементарного отрезка
![]() .
Покажем крупным планом элементарный
участок. Площадь под кривой заменяется
приближенно площадью под параболой
проведенной через точки A,B,C.
.
Покажем крупным планом элементарный
участок. Площадь под кривой заменяется
приближенно площадью под параболой
проведенной через точки A,B,C.
![]() .
Параболу можно определить разными
способами. В качестве параболы, проходящей
через три точки используем первый
интерполяционный полином Ньютона. Для
удобств преобразования рассмотрим
первый элемент участок [x0,x2],
тогда точки
.
Параболу можно определить разными
способами. В качестве параболы, проходящей
через три точки используем первый
интерполяционный полином Ньютона. Для
удобств преобразования рассмотрим
первый элемент участок [x0,x2],
тогда точки
A (x0,f(x0))=(x0,y0)
B (x1,y1)
C (x2,y2)
![]() ,
для удобства перейдем к переменной q
,
для удобства перейдем к переменной q
![]() ,
,
![]() ,
,
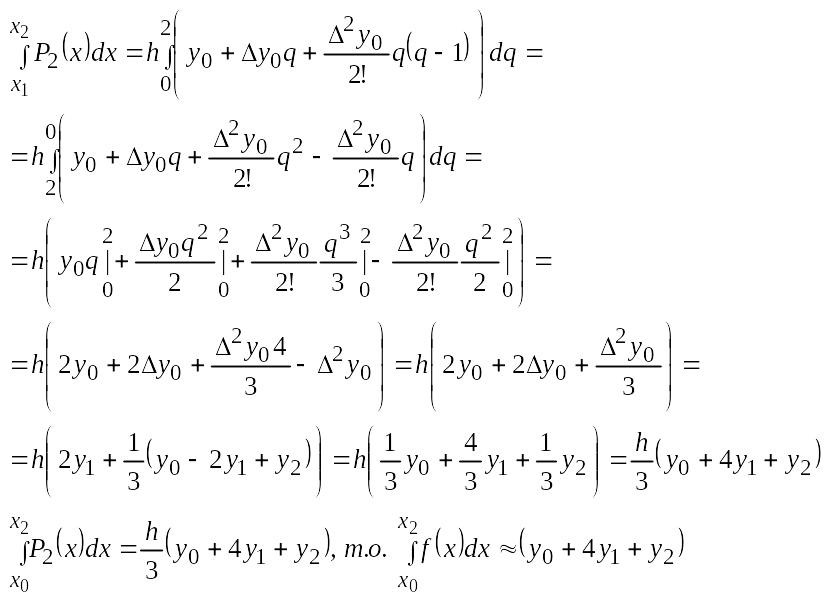
![]()
Обобщение этой формулы на произвольные случаи
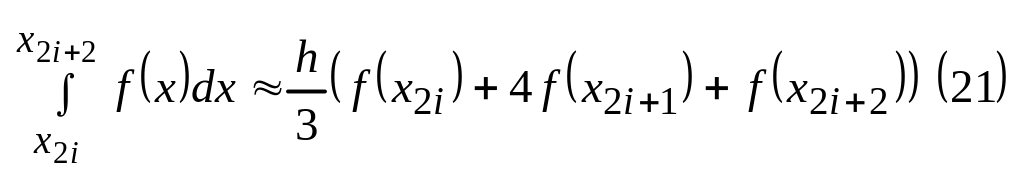 -малая
формула парабол (малая формула Симпсона)
-малая
формула парабол (малая формула Симпсона)
Интеграл на всем участке
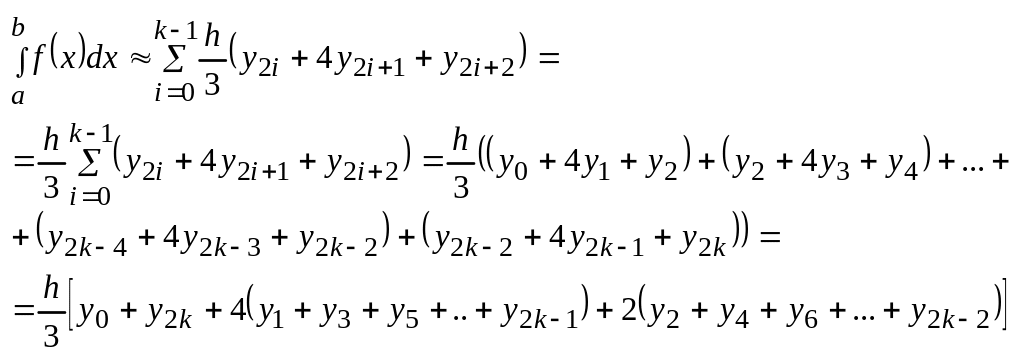 h=const
h=const
Т.о.
![]() -большая
ф-а парабол (Симпсона)
-большая
ф-а парабол (Симпсона)
Введем в рассмотрение величину
![]()
Теорема 3.
![]() класс
k-раз
непрерывно дифференцируемых функций
на отрезке [a;b]
класс
k-раз
непрерывно дифференцируемых функций
на отрезке [a;b]
Если
![]() 4 раза дифференцируема, то
4 раза дифференцируема, то
![]()
Вывод:
Сравнение методов прямоугольников, трапеций и парабол на основе теоремы 1,2,3 можно сделать следующий простой вывод. Самым грубым яв-ся метод прямоугольников, а самый точный среди рассмотренных – метод парабол.
Квадратурная формула называется точной, если ее R(f)=0.
