
- •20. Метод наименьших квадратов(мнк)
- •25. Численное дифференцирование. Метод неопределенных коэффициентов.
- •26. Формула численного дифференцирования, основанные на применении интерполяционных формула Лагранжа.
- •27. Численное интегрирование. Метод прямоугольников.
- •28. Численное интегрирование. Метод трапеций.
- •29. Численное интегрирование. Метод парабол.
- •30. Квадратурные формулы Ньютона-Котеса.
- •31. Задача Коши для обыкновенного дифференциального уравнения (оду) 1 порядка. Метод Эйлера.
- •32. Численное решение задачи Коши для оду 1 порядка методом Рунге-Кутта.
- •33. Система оду I порядка. Метод Эйлера.
- •34. Система оду I порядка. Метод Рунге-Кутта.
- •35. Конечно-разностный метод решения дифференциальных ур-ий I порядка. Построение конечно-разностной схемы.
- •36. Краевая задача для линейного обыкновенного дифференциального ур-я II порядка. Построение конечно- разностной схемы.
- •37. Первая краевая задача для уравнения теплопроводности. Явная конечно – разностная схема.
- •38. Первая краевая задача для уравнения теплопроводности. Неявная конечно-разностная схема.
- •41. Краевая задача для диф. Ур-ий частных производных
38. Первая краевая задача для уравнения теплопроводности. Неявная конечно-разностная схема.
![]() оно
дополняется нач условием
оно
дополняется нач условием
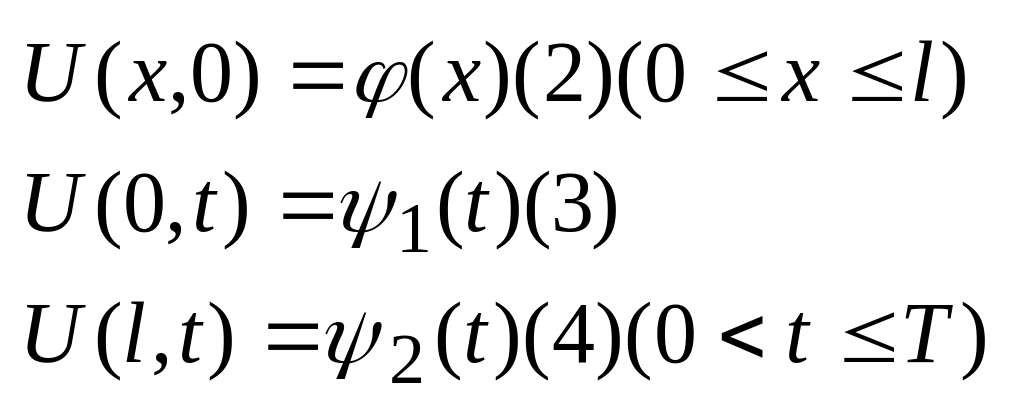
![]()
![]()
![]()
![]() -известные
функции l
– длина стержня T
– верхние граница временного промежутка
-известные
функции l
– длина стержня T
– верхние граница временного промежутка
![]() -
искомое решение температура в точке x
стержне в момент времени t
-
искомое решение температура в точке x
стержне в момент времени t
1) создадим сетку [0,l] :n [0,t]:m tj=jτ,
Неявная схема.
Произвольные внутренние точки мы заменим следующим образом

![]() количество уравнение
вида (7) равно количеству внутренних
узловых точек m(n-1)
преобразуем уравнение, введем в
рассмотрение
количество уравнение
вида (7) равно количеству внутренних
узловых точек m(n-1)
преобразуем уравнение, введем в
рассмотрение
![]()
![]() Шаблон
Шаблон
Уравнение (9) содержит
3 значения искомого решение из j-го
слоя, поэтому нельзя явно выразить
искомое решение через известное значение.
Для нахождения искомого решения на j
слоя необходимо решить систему уравнений
поэтому Даная схема называется не явной
схемой![]()
Краевые условия
(2),(3),(4) заменим соответствующим дискретными
аналогоми. В эти условия производные
не входят поэтому они не заменяются
точно через значения функции
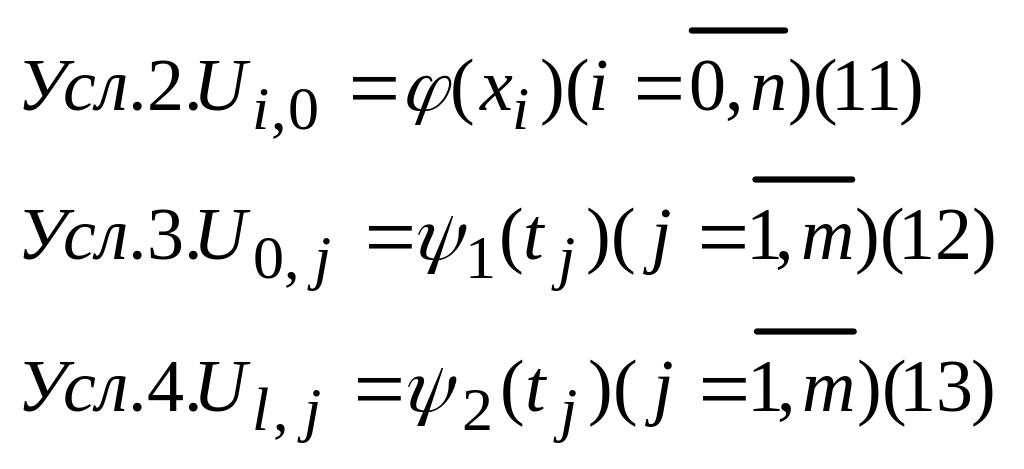 в
результате получаем полную систему
уравнений для произвольного слоя, с
помощью условий (12) (13) запишем уравнение
(10) в близи левой границы и правой границы
i=1
в
результате получаем полную систему
уравнений для произвольного слоя, с
помощью условий (12) (13) запишем уравнение
(10) в близи левой границы и правой границы
i=1![]()
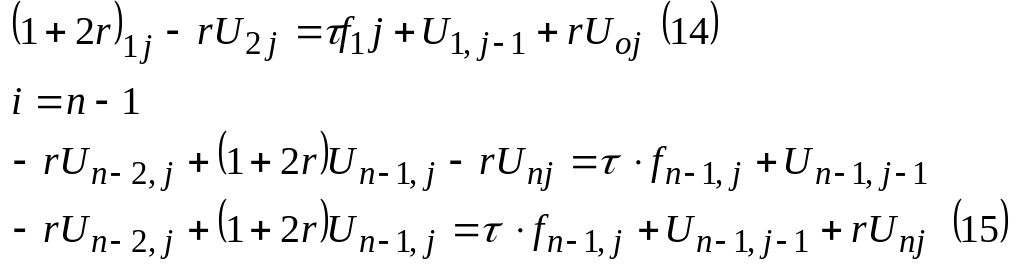
Тогда в ур-ие (10)
![]()
Для произвольного j-го слоя системы (16)
![]()
![]()
Система Ур-ий с 3х диагональной матрицей эффективно решается методом прогонки.
1+2r,
![]() >0
>0
Найдем сумму модулей недиагональных элементов:
1+2r>r+r;
1+2r>2r для любых r (17)
Матрица системы имеет диагональное преобладание при любом r. Поэтому матрица системы (16) яв-ся невырожденной, т.е. определитель не равен 0. Это означает, что система (16) однозначна разрешима при любом r. (одно решение). Таким образом имеет место своство:
Неявная схема всегда устойчива и имеет единственное решение при любом r. Это свойство позволяет проводить вычисления на крупных сетках. В явной схеме , здесь r-произвольно.
Алгоритм реализации неявной схемы.
1) Сначала рассчитаем искомое решение на начальном слое левой и правой границе. С помощью формул (11,12,13).
2) j=1
3) решается система (16) методом прогонки.
4) j=j+1
5)Если
![]() ,
то идти к пункту 3, иначе идти к пункту
6.
,
то идти к пункту 3, иначе идти к пункту
6.
6) вывод полученных результатов.
41. Краевая задача для диф. Ур-ий частных производных
Диф. уравнения часто используется при моделирования технологических процессов различных физических явлений и т.д. Для однозначного определения процесса к этим уравнениям необходимо присоединить дополнительное условие. Математически это связано с тем что при интегрировании диф. уравнения явл-ся константа интегрирования. Для определения этих констант как раз нужны эти дополнительные условия. Дополнительные условия называют краевыми условиями. Краевые условия делятся на начальные и граничные условия. Начальные условие определяют искомое решение в некоторый начальный момент времени. При t=t0
Граничное условие определяют поведение искомого решения на границе области. В свою очередь они могут быть одного из трех видов :
1) Граничное условие первого рода.
Пусть для определенности искомое решение яв-ся функцией от двух переменных U=U(x,y).
Д – внутренняя область.
Г – граница области
Математически
граничное условие первого рода
записывается в виде
![]() ,
здесь
,
здесь
![]() -известная
функция. В частности она может быть
константой. Другими словами в этом
случае известны значения искомого
решения на границе области
-известная
функция. В частности она может быть
константой. Другими словами в этом
случае известны значения искомого
решения на границе области
2. Граничные условия 2 рода
Математически
запишется следующим образом
![]()
n-нормаль к границе, нормальный вектор
Другими словами на границе области известны значения производного по нормали.
3. Граничное условие III рода.
Математическая
запись
![]()
В этом случае задана
минимальная комбинация значений искомого
решения производной по нормали на
границе области.
![]() -константа.
Эти граничные условия представляют
собой граничное условие более общего
вида .Предыдущее условие 1,2 рода могут
быть получены как частные случаи условие
3 рода. Если положим
-константа.
Эти граничные условия представляют
собой граничное условие более общего
вида .Предыдущее условие 1,2 рода могут
быть получены как частные случаи условие
3 рода. Если положим
![]() ,
получим первого рода.
,
получим первого рода.
![]() получим
условие второго рода. В соответствии с
существующей классификацией различают
следующие краевые задачи.
получим
условие второго рода. В соответствии с
существующей классификацией различают
следующие краевые задачи.
1 задача с начальными условиями (задача Коши).
Граничное условие полностью отсутствует. Обычно начальное условие присутствует в не стационарных краевых задачах.
2. задача с граничными условиями.
При этом граничное
условие могут быть одного из 3х
рассматриваемых видов. Например, если
рассматривается диф уравнение, то к
нему могут быть поставлены различные
граничные условия
![]() Оператор
Лапласа
Оператор
Лапласа
![]()
Если к этому
уравнению ставиться граничные условия
первого рода, то краевую задачу называют
задачей Дирихле![]() -
Задача Дирихле. Если известна производная
по нормали, то эта задача Неймана.
-
Задача Дирихле. Если известна производная
по нормали, то эта задача Неймана.![]() -
закон Неймана. Смешанная краевая задача.
В такой задаче одновременно присутствуют
начальные и граничные условия, то есть
эта задача является более общей краевой
задачей.
-
закон Неймана. Смешанная краевая задача.
В такой задаче одновременно присутствуют
начальные и граничные условия, то есть
эта задача является более общей краевой
задачей.
