36. Краевая задача для линейного обыкновенного дифференциального ур-я II порядка. Построение конечно- разностной схемы.

Процесс решения задачи с помощью МКР условно можно разбить на несколько этапов:

1. создание сетки. 2. Аппроксимация производных входящих в дифференциальные ур-я в узлах сетки. 3. замена исходного диф уравнения система конечно-разностных ур-ий (КРУ). Т.е. исходное Ур-е заменяется системой алгебраических уравнений относительно значений искомого решения в узлах сетки для замыкания этой системы уравнений используются краевые условия, присутствующие в задаче. 4. решение системы алгебраических Ур-ий полученных, на предыдущем этапе. В зависимости от уравнения эта система может быть системой линейных или не линейных уравнений. Следует заметить что существует один важный этап это исследование устойчивости сходимости решения.

Рассмотрим краевую задачу для линейного обыкновенно дифференциального уравнения II порядка.

Условие на левой границе

На правой

Здесь p(x), q(x), f(x) – известные функции

C₁,C₂,d₁,d₂,g₁,g₂- известные константы

a,b – известны

y(x)-? – искомое решение

такую задачу наз-ют 2^х точечной краевой задачей.

1. область одномерная, отрезок [a;b] разобьем на n-равных частей.

Условие (23) на левой границе.

Условие (24) на правой границе.

2. Для аппроксимации производных 1 и 2 порядка, входящих в исходное Ур-е используем формулу центральной разности.

Берем произвольную внутриузловую точку .

Исходное уравнение заменим соответствующим конечно разностных уравнений.

3.

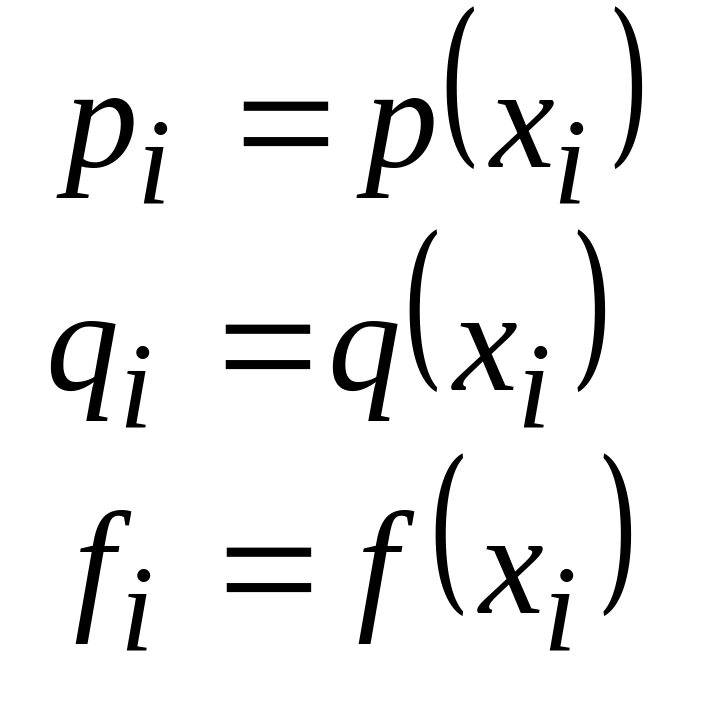
Количество уравнений вида (25) равно количеству внутренних узловых точек, т.е. n-1

Преобразуем полученное уравнение умножим на h².

Сгруппируем подобные члены

для удобство введем в рассмотрение коэффициент

i=(1,n-1)

Используя (28) перепишем (27)

Неизвестными являются y₀,y₁,…,y_n -? (n+1) неизвестно.

Для замыкания системы уравнений используем граничные условия (23), (24).

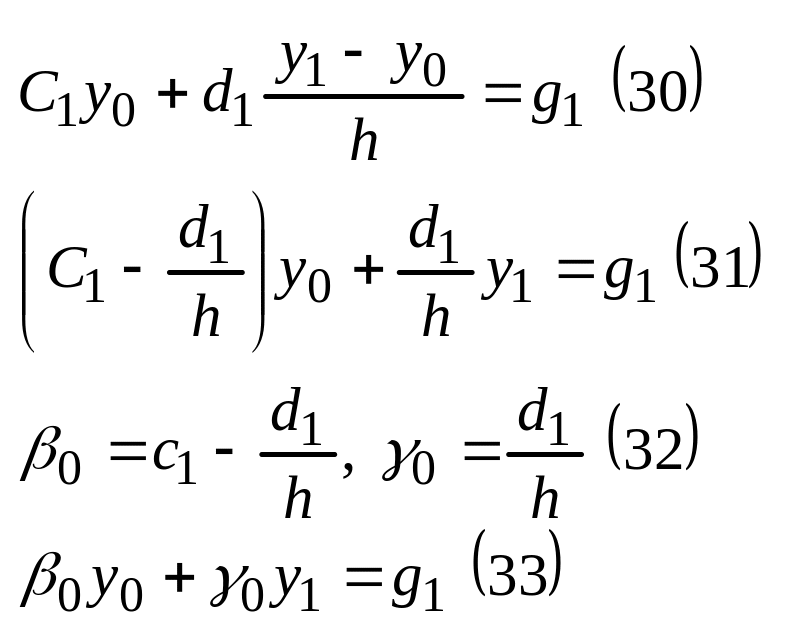
Усл (24)

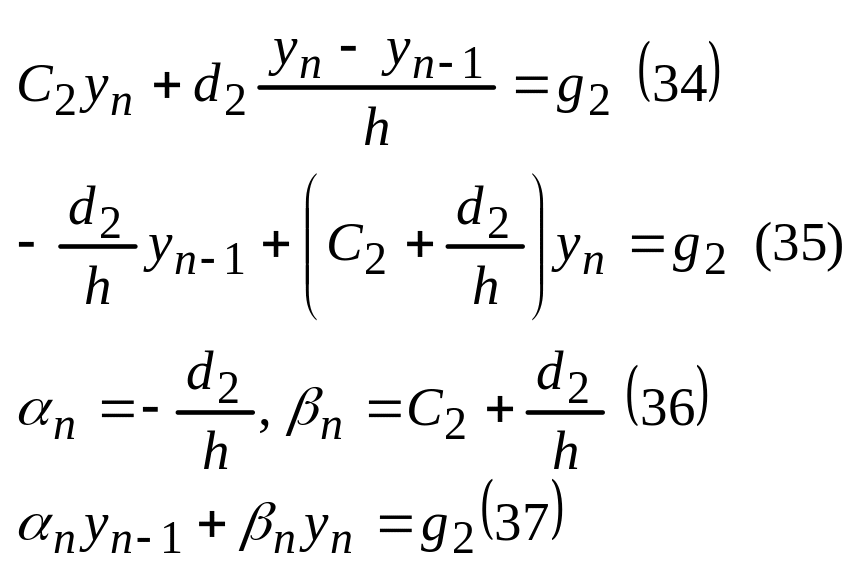
Матрица полученной системы является трехдиагональной такие системы обычно решаются методом прогонки. Решив полученную системы уравнений определяем значение искомое решение в узлах сетки. Если матрица системы имеет диагональное преобладание, то определитель не равен 0 и система имеет единственное решение.

Если то очевидно

Учитывая это можно задать условие относительно функции p и шага сетки.

37. Первая краевая задача для уравнения теплопроводности. Явная конечно – разностная схема.

Первая краевая задача для уравнения теплопроводности.

Под первой краевой задачей лдя такого уравнения понимают следующую краевую задачу 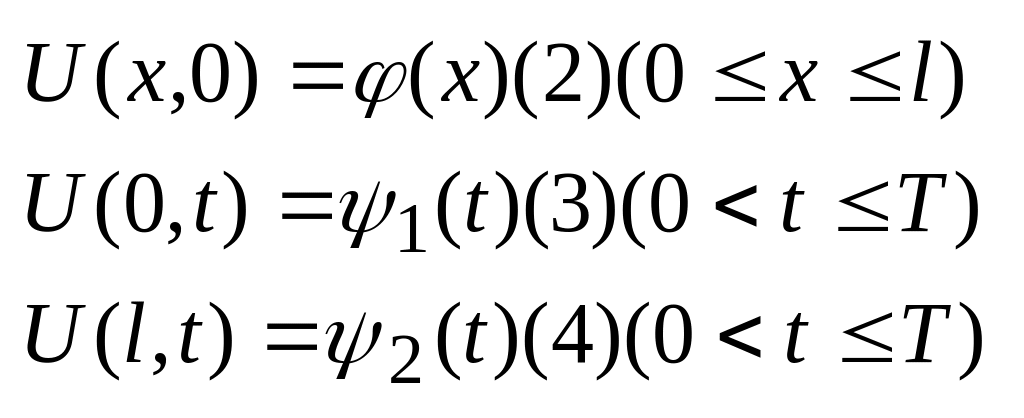Здесь f(x,t),φ(x),ψ₁(t), ψ₂(t) известные функции , l- длинна стержня T- верхняяграница временного промежутка, U(x,t)- искомое решение т.е. задача рассматривается в прямоугольнике. Физический смысл U(x,t) температура в точке стержня в момент времени t. f(x,t) характеризует источники тепла, стоки тепла. Условие 2) задает начальное распределение температуры при t=0 U(x,0) . Условие 3 Граничное условие задает распределение температуры на левой границе в различные моменты времени U(0,t) . Условие 4 задает распределение температуры на правой границе в различные моменты времени U(l,t) Найдем решение краевой задачи метод конечных разностей 1) создадим сетку [0,l] :n [0,t]:m t_j=jτ, проведем отрезки x_i,t_j сетка равномерная в каждом из направлений способа апроксимации производных 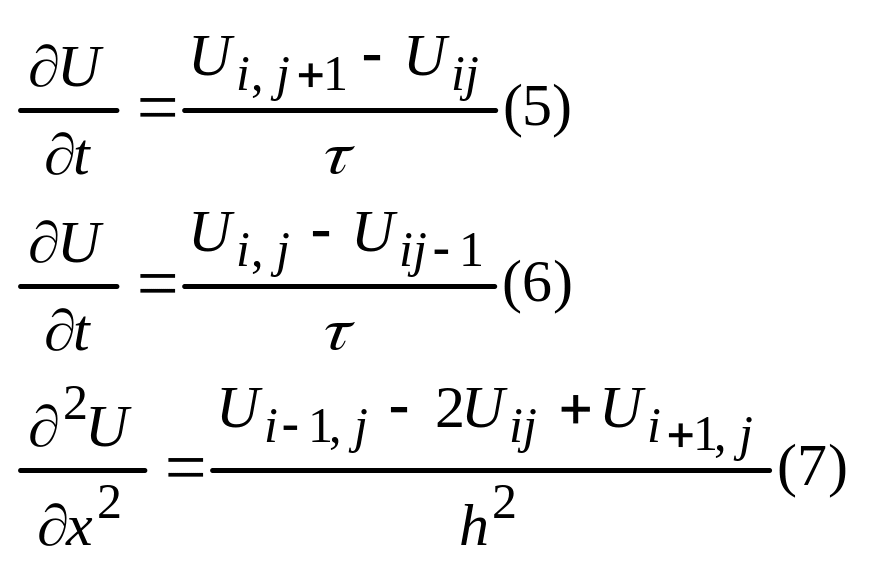В зависимости от использования формул (5), (7), или (6),(7) получается различные конечно разностные схемы (КРС). Определение: Шаблоном называется схема временного расположения узловых точек, использованных при конечно разностной апроксимации диф уравнения. Явная схема[(5),(7)].

Произвольные внутренние узловые точки уравнения (1)заменим конечно разностным уравнением используя формулу (5),(7) 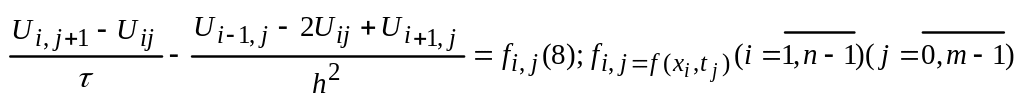количество таких уравнений равно количеству внутренних узловых точек m(n-1) преобразуем это уравнение умножим на τ и введем в рассмотрение параметр в это уравнение входит только одно значение искомого решения из (j+1) слоя(i,j+1).

Рассмотренное на рисунке его можно сдвинуть в право. Из уравнения (10) можно явно определить значение искомого решения из (j+1) Где I,j меняется в указанных пределах. К этим уравнениям присоединим дискретные аналоги краевых условий в эти условия производные не входят, поэтому они заменяются точно через значение функции

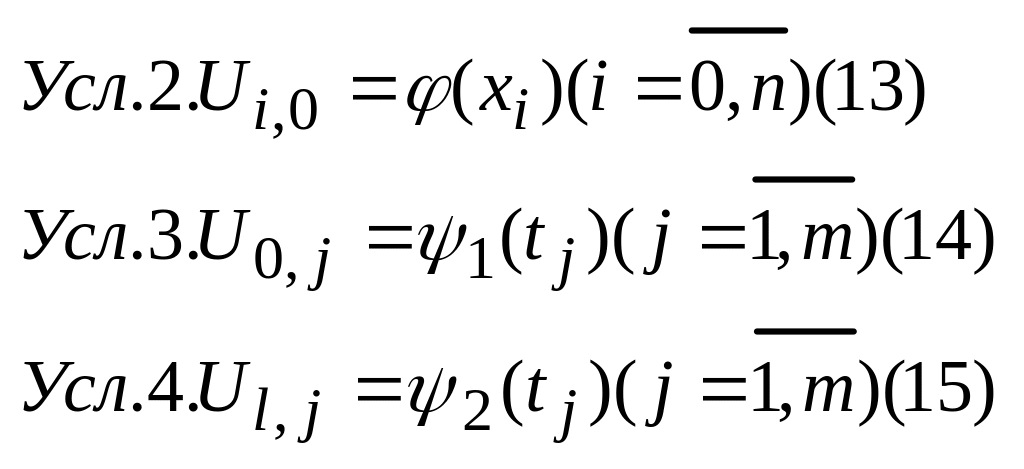В результате получим полностью замкнутую систему уравнений.

Алгоритм реализации явной схемы

1) Определим искомое решение на начальном слое, левой и правой границы по формулам (13,14,15)

2) j=0

3) u_i,j+1 = по формуле (12) . Меняем i, рассчистаем искомое решение на очередном слое.

4) увеличиваем j на единицу j=j+1

5) Если , то идти к пункту 3 иначе идти к пункту 6

6) Вывод полученных результатов, завершение работы.

Явная схема реализуется просто однако она имеет недостаток:

Свойство 1. явная схема имеет единственное решение и устойчиво при , при r>1/2, явная схема не устойчивая.

Это свойство накладывает ограничение на выбор временного и пространственного шагов.