3. Оптимальные системы.

3.1. Статическая оптимизация

Оптимизация – поиск наилучшего решения. Чтобы выделить наилучшее решение из всех возможных, использует математическое выражение, которое называют критерий оптимальности, критерий качества, функция цели. Оптимальным является такое решение, которому соответствует экстремальное значение критерия.

В зависимости от математической природы критерия оптимальности, различают статическую и динамическую оптимизации.

В статической оптимизации критерием оптимальности является некая функция Q одной или нескольких переменных. Ёе называют функцией цели, целевой функцией. Каждая задача имеет свой набор переменных, свои условия. Поэтому целевую функцию приходится формировать для каждой задачи. Оптимизация заключается в том, что ищут такие значения переменных, которые делают целевую функцию экстремальной.

Надо отличать понятие “экстремальной” от понятий “наибольшее и наименьшее значение”. В точках экстремума производная целевой функции равна нулю. В точках наибольшего или наименьшего значения производная не равна нулю.

Рассмотрим пример.

На рис. 3.1. изображена целевая функция

Точки А и D – границы функции. В точке А функция имеет наименьшее значение, Q = -4. В точке D – наибольшее, Q = 3. в каждой из точек .

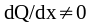Точки В и С находятся внутри границ изменяя функции . В каждой из них . То есть, в этих точках функция не меняется. Именно такие точки могут быть экстремальными. В точке В локальный максимум, Q = 2, в точке С - локальный минимум, Q = -2.

В разобранном примере функция цели зависит от одного аргумента. Если функция цели зависит от множества аргументов, их представляют в виде вектора переменных.

.

Функцию цели записывают матрицей Q(X). В точке экстремума вектор переменных принимает значение X^*. Условие экстремума записывается матричным уравнением в форме

,

или в форме

. (3.1)

Выражение (5.1.) – это система алгебраических уравнений. Она имеет решение в виде вектора оптимальных значений переменных .

Какое экстремальное значение имеет функция цели, указывает вторая производная Условием минимума является

, (3.2)

условием максимума

. (3.3)

Если

. (3.4)

то это точка перегиба. Производные частные, берутся по каждой переменной.

Безусловная оптимизация

Целевая функция может зависеть более чем от одной переменной: . Если эти переменные изменяются независимо друг от друга, поиск экстремума проводится только посредством целевой функции. Никаких условий на изменение переменных не накладывается. Такая оптимизация называется безусловной.

Иллюстрацией будет следующий пример.

Для изготовления ёмкости в виде конуса заготовлен металлический лист в виде круга радиусом R, рис. 3.2 а.

Из круга надо вырезать сектор с углом α и свернуть лист в конус. Параметры конуса указаны на рис.3.2 б. Сектор с углом какой величины надо вырезать, чтобы получить максимальный объем конуса V?

Цель – получить максимальный объём, значит V – целевая функция.

Из формулы объема

(3.5)

видно, что целевая функция задачи зависит от двух переменных: V(r,h). Они могут изменяться независимо одна от другой. То есть это задача на безусловную оптимизацию.

Параметры конуса и параметры заготовки связаны между собой. Длина окружности основания конуса 2r равна длине окружности заготовки 2R за вычетом длины дуги сектора l: 2r = 2R  l . Учитывая, что

.

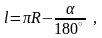получаем:

Выразим высоту конуса через радиус заготовки. Из прямоугольника на рис. 3.2.б выводим:

Заменив в (3.5) r по (3.6) и h по (3.7) получим объем конуса, как функцию параметров заготовки:

Для удобства вычислений обозначим 1 - /360 = х и будем искать экстремум целевой функции.

Потребуем, чтобы . Получим уравнение

Его корни x₁ = 0, x_2,3 = ±0,82 доставляют целевой функции экстремум. Оптимальное значение угла сектора α, максимизирующее объём конуса, равно

, α = 65^о

Вывод: Статическая безусловная оптимизация заключается в том, что определяют функцию цели, выражают её через параметры задачи, находят экстремум и определяют максимум.