
- •Билет №1
- •Билет №2
- •Билет №3
- •Билет №4
- •Билет №5
- •Билет №6
- •Билет №7
- •Билет №8
- •Билет №9
- •Билет №10
- •Билет №11
- •Билет №12
- •Билет №13
- •Билет №14
- •Билет №15
- •Билет №16
- •Билет №17 Число опорных решений канонической задачи линейного программирования
- •Билет №18
- •Билет №19
- •Билет №20
- •Билет №21
- •Билет №22
- •Билет №23
- •Билет №24
- •Билет №25
- •Билет №26
- •Билет №27
- •Билет №28
- •Билет №29
- •Билет №30
- •Билет №31
- •Билет №32
Билет №5
Решение системы однородных уравнений
Линейное
уравнение называется однородным,
если его свободный член равен нулю, и
неоднородным
в противном случае. Система, состоящая
из однородных уравнений, называется
однородной и имеет общий вид:

Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.
Доказательство:
Допустим, система, ранг которой равен
![]() ,
имеет ненулевое решение. Очевидно, что
,
имеет ненулевое решение. Очевидно, что
![]() не
превосходит
не
превосходит
![]() .
В случае
.
В случае
![]() система
имеет единственное решение. Поскольку
система однородных линейных уравнений
всегда имеет нулевое решение, то именно
нулевое решение и будет этим единственным
решением. Таким образом, ненулевые
решения возможны только при
система
имеет единственное решение. Поскольку
система однородных линейных уравнений
всегда имеет нулевое решение, то именно
нулевое решение и будет этим единственным
решением. Таким образом, ненулевые
решения возможны только при
![]() .
.
Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Доказательство:
Если у системы уравнений
![]() ,
то ранг
системы
не превышает числа уравнений
,
то ранг
системы
не превышает числа уравнений
![]() ,
т.е.
,
т.е.
![]() .
Таким образом, выполняется условие
и,
значит, система имеет ненулевое решение.
.
Таким образом, выполняется условие
и,
значит, система имеет ненулевое решение.
Следствие 2: Однородная система уравнений с неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.
Доказательство:
Допустим, система
линейных
однородных уравнений, матрица которой
![]() с
определителем
с
определителем
![]() ,
имеет ненулевое решение. Тогда по
доказанной теореме
,
а это значит, что матрица
,
имеет ненулевое решение. Тогда по
доказанной теореме
,
а это значит, что матрица
![]() вырожденная,
т.е.
вырожденная,
т.е.
![]() .
.
Билет №6
Примеры линейно зависимых и линейно независимых систем векторов
Система m-мерных векторов
 называется линейно
зависимой,
если система линейных уравнений (1)
называется линейно
зависимой,
если система линейных уравнений (1) 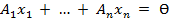 имеет ненулевые решения. Если же система
(1) не имеет ненулевых решений, то данная
система векторов
является линейно
независимой.
имеет ненулевые решения. Если же система
(1) не имеет ненулевых решений, то данная
система векторов
является линейно
независимой.Система m-мерных векторов называется линейно зависимой, если существует такой ненулевой вектор
 ,
что выполняется
линейное соотношение (2)
,
что выполняется
линейное соотношение (2)  .
Если же из
всякого соотношения вида (2) следует,
что
.
Если же из
всякого соотношения вида (2) следует,
что  ,
то система
векторов
,
то система
векторов  называется
линейно
независимой.
называется
линейно
независимой.
Пример:
Билет №7
Свойства системы векторов и части этой системы
Из определения линейной зависимости векторов следует, что любая система векторов либо линейно зависима, либо линейно независима.
Если часть данной системы векторов
 линейно
зависима, то и вся данная система линейно
зависима.
линейно
зависима, то и вся данная система линейно
зависима.
∆ Пусть A1, …, Al линейно зависимая часть системы векторов A1, …, An , где l<n. По определению найдется такой вектор К=(k1, …, kl) ≠ Ɵ, что будет выполняться соотношение A1k1 + … + Alkl = Ɵ. Тогда соотношение вида A1k1 + … + Alkl + … + + Ankn = Ɵ будет выполняться при
К=(k1, …, kl, 0, …, 0) ≠ Ɵ. Следовательно, по определению вся система векторов A1, …, An является линейно зависимой. ∎
Если данная система векторов линейно независима, то и любая ее часть линейно независима.
∆ От противного. Пусть часть A1, …, Ak данной системы векторов A1, …, An является линейно зависимой. Тогда из 2 свойства следует, что вся данная система векторов линейно зависимая. Это противоречит условию, следовательно, предположение неверно, а верно то, что любая часть линейно независимой системы является тоже линейно независимой. ∎
Если система векторов A1, …, An, B является линейно зависимой, а ее часть A1, …, An – линейно независима, то вектор
 линейно выражается через векторы
A1,
…, An.
линейно выражается через векторы
A1,
…, An.
∆ Система векторов
A1,
…, An,
B
является линейно
зависимой. Тогда по определению найдется
такой вектор К=(k1,
…, kn,
kn+1)
≠ Ɵ , что
выполняется соотношение A1k1
+ … + Ankn
+ Bkn+1
= Ɵ. Покажем,
что kn+1
≠ 0. Если
бы kn+1
= 0,
то Bkn+1
= Ɵ.
Тогда A1k1
+ … + Ankn
= Ɵ, а т. к. система
векторов A1,
…, An
по условию
линейно независима, то k1
= … = kn
= 0, а следовательно,
вектор
,
что противоречит тому, что К=(k1,
…, kn,
kn+1)
≠ Ɵ. Т. о. kn+1
≠ Ɵ. Тогда можно
записать B
=A1
(-k1/kn+1)
+ … + An
(-kn/kn+1)![]() ∎
∎
