Билет №20

Свойства симплекс таблицы: структура вектора ограничений, оценки базисных векторов и значение целевой функции

1°. Если симплекс таблица приведена к базису Аі₁, Аі₂, …, Аіr опорного решения α, то в столбце В΄ находятся координаты опорного решения α, соответствующие векторам базиса Аі₁, Аі₂, …, Аіr, то есть α₁=αі₁, α₂=αі₂, …, αr=αіr.

Так как вектор α=(0,0,…,0,αі₁,0,0,…,0,αі₂,0,0,…,0,αіr,0,0,…,0) является опорным решением задачи (1)-(3),то он является и допустимым решением этой задачи , а следовательно, является решением системы линейных уравнений (2),то есть выполняется соотношение:

(6) Аі₁ α₁+Аі₂ α₂+…+Аіr αr=В.

Решением системы (5) является вектор α΄=(0,0,…,0,α₁,0,0,…,0,α₂,0,0,…,0,0,αr,0,0,…,0). Системы (5) и (4) равносильны, так как получены одна из другой методом Гаусса. Поэтому вектор α΄ является решением системы(4),и, следовательно, выполняется соотношение :

(7) Аі₁ αі₁+Аі₂ αі₂+…+Аіr αіr=В.

Вычитая из соотношения (6) соотношение (7), получаем соотношение:

(8) Аі₁ (αі₁-α₁)+Аі₂ (αі₂-α₂)+…+Аіr (αіr-αr)=Ѳ.

Так как векторы Аі₁,Аі₂,…,Аіr являются базисом системы векторов условий задачи (1)-(3), то они линейно независимы. Следовательно, соотношение (8) возможно, при αі₁-α₁=0, αі₂-α₂=0,…,αіr-α₁=0.

Откуда,αі₁=α₁, αі₂=α₂,…,αіr=α₁.

2°. Оценки базисных векторов опорного решения всегда равны нулю, то есть, если векторы Аі₁, Аі₂,…,Аіr являются базисом некоторого опорного решения задачи (1)-(3), то δі₁=δі₂=…,=δіr.

Доказательство следует из построения строки оценок системы векторов условий, приведенных к базису опорного решения.

3°. Если симплекс таблица приведена к базису опорного решения α, то δ₀=f(α).

Из построения строки оценок для системы векторов условий задачи (1)-(3), приведенной к базису Аі₁, Аі₂, …Аіr, и с учетом того, что α₁=αі₁, αі₂, …, α₁=αіr.

Билет №21

Лемма о целевой функции

Пусть δ₁,…,δј,…,δn оценки векторов условий задачи (1)-(3), приведенных к базису опорного решения α. Если вектор β=(l₁,…,lј,…,ln) является допустимым решением данной задачи, то f(β)=f(α)-∑ δј lј.

Пусть векторы А₁, А₂, …, Аr являются базисом опорного решения α=(α₁,α₂,…,αr,0,0,…,0). Тогда симплекс таблица системы векторов условий задачи(1)-(3), приведенных к данному базису будет иметь вид:

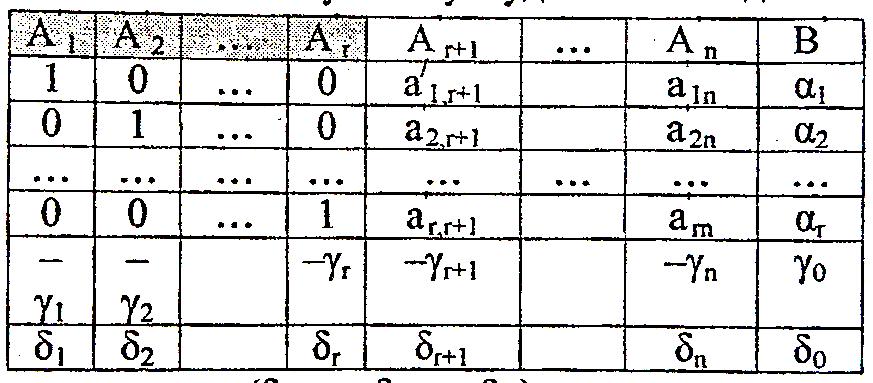
Где по правилу построения строки (δ₁,…,δј,…,δn), оценки примут следующие значения: δ₁=δ₂=…=δr=0 и

Так как для базисных векторов А₁, А₂, …, Аr оценки равны нулю, то есть δ₁=δ₂=…=δr=0, то значение целевой функции на векторе β можно записать в виде:

f(β)= γ₀+γ₁α₁+…+γr αr-δ r+₁ l r+₁- δ r+₂ l r+₂-…-δn ln=f(α)-∑ δј lј.

Билет №22

Достаточное условие оптимальности опорного решения канонической задачи линейного программирования на минимум

Если для опорного решения α⁰ канонической задачи линейного программирования на минимум

1. f(X) =

2. 

3. 

Найдется базис, для которого все оценки неположительные, то есть то вектор α⁰ является оптимальным решением данной задачи.

Доказательство. Пусть – оценки системы векторов условий, приведенных к некоторому базису опорного решения α⁰ . Если вектор β=(l_1, …, l_j, …, l_n) является произвольным допустимым решением канонической задачи линейного программирования (1)-(3), то по доказанной лемме имеем : f(β) = f(α) - . Так как для любых j=1,2,…,n по условию , а вектор β=(l_1, …, l_j, …, l_n) является произвольным допустимым решением данной задачи, т.е. для всех j = 1,2,…,n, то f(β)≥f(α⁰). Следовательно, по определению вектор α⁰ является оптимальным решением задачи (1)-(3) на минимум.