Билет №21
2.
Теорема
о существовании первообразной функции.
Для любой непрерывной функции существует
бесконечное множество первообразных
функций, отличающихся друг от друга на
постоянную величину.Д о к а з а т е л ь с
т в о. 1. Покажем, что для функции
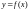существует первообразная функция
,
являющаяся площадью криволинейной
трапеции с переменной граничной прямой.
Пусть
правая граничная прямая изменяет
положение от х
до
.
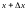На этом отрезке
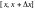непрерывная функция
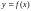достигает своего наибольшего М
и наименьшего m
значений
,
.Очевидно,
значение площади элементарной
криволинейной трапеции
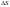на отрезке
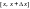удовлетворяет неравенству
.
Поделим это неравенство на
,
получим
.
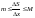При
наибольшее и наименьшее значения функции
на этом отрезке стремятся к одной и той
же величине
,
.
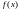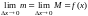По теореме о промежуточной функции
,
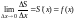т. е.
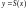является первообразной для функции
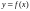.2.
Покажем, что для данной функции существует
бесконечное множество первообразных
функций. Действительно, если к данной
функции прибавить любую постоянную
величину, то ее производная не изменится
,
.3.
Покажем также, что любые две первообразные
функции отличаются друг от друга на
постоянную величину. Пусть
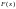и
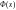первообразные функции для
.
Тогда
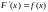и
.
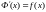Найдем их разность, получим
.
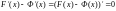Если производная функции равна нулю,
то функция является постоянной.
Следовательно,
,
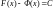где
,
и
.
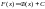3.Интегральный
признак Коши.Если
члены знакоположительного ряда
,
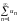являющиеся значениями функции
целочисленного аргумента
,
монотонно убывают и стремятся к нулю
,
то: 1) если
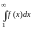сходится, то и ряд
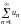сходится; 2) если
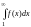расходится, то и ряд
расходится. Д о к а з а т е л ь с т в о. В
прямоугольной декартовой системе
координат
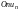непрерывная кривая
проходит через точки
и ограничивает сверху криволинейную
трапецию ABCD
(рис. 86). Площадь этой криволинейной
трапеции равняется
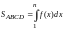.Построим
две ступенчатые фигуры с угловыми
точками
.
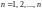Эти ступенчатые фигуры состоят из
прямоугольников, основания которых
равняются единице, а высоты значениям
.
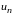Н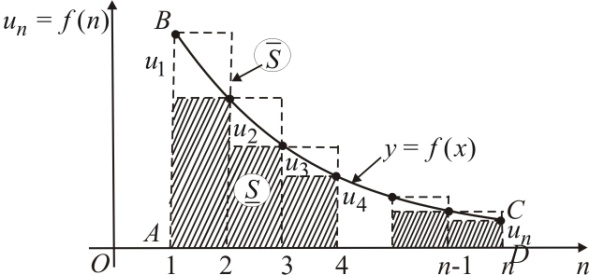
айдем
площади этих фигур.
,
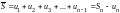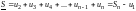,где
n-я
частичная сумма ряда. Площади этих
ступенчатых фигур ограничивают площадь
криволинейной трапеции ABCD
снизу и сверху
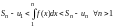.Рассмотрим
левую часть этого неравенства
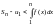
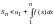.При
неограниченном возрастании числа n
членов ряда частичные суммы ряда
монотонно возрастают, так как ряд
знакоположительный. При этом интеграл
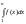также возрастает и ограничен величиной
интеграла
.
Поэтому
,
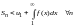т. е. последовательность частичных сумм
ограничена. По теореме Вейерштрасса
существует предел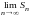
.
Следовательно, ряд сходится. Рассмотрим
правую часть неравенства
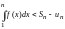
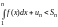.По
условию теоремы
.
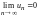Если
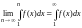неограниченно возрастает, то и предел
частичных сумм
неограниченно возрастает и, следовательно,
ряд расходится.Таким образом, интегральный
признак Коши в принципе позволяет для
любого ряда решить вопрос о его сходимости.
Трудность в его применении заключается
в нахождении несобственных интегралов.
Возможности в их нахождении ограниченные.
Билет
22.1.Бесконечно малые и бесконечно большие
функции, взаимосвязь между ними. Свойства
бесконечно малых функций. Определение
бесконечно малой функции.
Функция (x)
называется бесконечно малой функцией
при
,
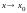если для любого сколь угодно малого
положительного числа
существует такое положительное число
,
зависящее от ,
что для любого x,
принадлежащего
-окрестности
(x)
находится в -окрестности
начала координат (x)
,
т.е.
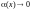.Определение
бесконечно большой функции.
Функция
называется бесконечно большой при
,
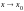если для любого сколь угодно большого
положительного числа N
существует такое положительное число
,
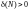зависящее от N,
что если x
принадлежит -окрестности
числа
(
),
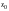то абсолютная величина значения
функции больше числа N
(
),
т.е.
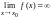. Теорема
1.2. Функция,
обратная по величине к бесконечно малой
функции является бесконечно большой
и, наоборот, функция, обратная по величине
к бесконечно большой, является бесконечно
малой функцией.Свойства
бесконечно малых функций Свойство
1. Сумма конечного числа бесконечно
малых функций является бесконечно малой
функцией.Свойство
2. Произведение бесконечно малой функции
на ограниченную функцию
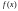является бесконечно малой функцией.Следствие
1. Произведение
бесконечно малой функции
на постоянную величину С
является бесконечно малой функцией, т.
е.
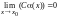.Следствие
2. Произведение
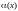бесконечно малых функций
и
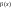является бесконечно малой функцией.Свойство
3. Частное от деления бесконечно малой
функции
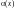на функцию
,
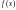предел которой отличен от нуля (
)
является бесконечно малой функцией.
2.
Дифференциальные уравнения. Основные
понятия. Нахождение уравнения по его
решению.Уравнение
называется дифференциальным, если оно
содержит производные или дифференциалы
искомой функции, искомую функцию и
независимую переменную.В общем случае
дифференциальное уравнение имеет вид:
или
.
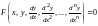Порядком дифференциального уравнения называется наивысший порядок производных искомой функции, входящей в уравнение
Дифференциальное
уравнение называется обыкновенным,
если искомая функция зависит от одной
переменной. Приведенные выше
дифференциальные уравнения
обыкновенные.Дифференциальное уравнение
называется уравнением в частных
производных,
если искомая функция зависит от нескольких
переменных.Дифференциальное уравнение
называется линейным,
если оно линейное относительно искомой
функции и ее производных, т. е. функция
и ее производные входят в уравнение
только в первой степени.В общем случае
линейное дифференциальное уравнение
имеет вид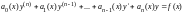
,где
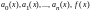
непрерывные функции.Если в этом уравнении
правая часть
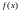равна нулю, то уравнение называется
однородным,
иначе неоднородным. Например,
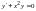
линейное однородное уравнение,
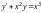
линейное неоднородное уравнение.Дифференциальное
уравнение называется нелинейным,
если оно является нелинейным относительно
искомой функции или ее производных.Решением
дифференциального уравнения называется
любая функция, которая при подстановке
в уравнение обращает его в тождество.Общим
решением
дифференциального уравнения n-го
порядка называется решение данного
уравнения, содержащее столько произвольных
постоянных, независящих друг от друга,
каков порядок уравнения, т. е. n.Часто
общее решение дифференциального
уравнения невозможно найти в явном
виде, а можно получить его только в
неявной записи. Поэтому вводится понятие
общего интегралаОбщим
интегралом
дифференциального уравнения n-ого
порядка называется уравнение, получающееся
при интегрировании дифференциального
уравнения, не содержащее производных
и дифференциалов искомой функции, а
содержащее n
произвольных постоянных, независящих
друг от друга.Таким образом, общее
решение дифференциального уравнения
n-ого
порядка имеет вид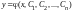
,а
общий интеграл
.Частным
решением
(интегралом) дифференциального уравнения
называется решение (интеграл), получающийся
из общего при конкретных значениях
произвольных постоянных.График частного
решения дифференциального уравнения
называется интегральной кривой.Общее
решение дифференциального уравнения
представляет семейство интегральных
кривых.Если известно общее решение или
общий интеграл, то можно найти
соответствующее им дифференциальное
уравнение.Пусть имеется общее решение
.
Для составления соответствующего ему
дифференциального уравнения необходимо
найти столько производных данного
решения, сколько произвольных постоянных
оно содержит. Тогда получится система,
состоящая из (n+1)-го
уравнения с n
произвольными постоянными
.
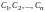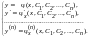Для
того чтобы получить соответствующее
дифференциальное уравнение, необходимо
в этой системе исключить произвольные
постоянные. Например, найти
из первых n
соотношений и подставить в последнее
3.
Ряд малорена. Остаточный член. Разложение
элементарных функций в степенной ряд
маклорена. Ряды Тейлора и Маклорена.Функция
разлагается в степенной ряд
в области G,
если он составлен для этой функции и
сходится к ней.Пусть степенной ряд
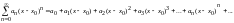Равномерно сходится к функции
,
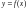т. е.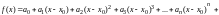
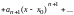Тогда его можно почленно дифференцировать.
Найдем производные этого ряда и подставим
значение
в эти соотношения
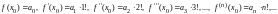,получим
формулы для нахождения коэффициентов
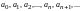
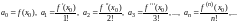
Следовательно,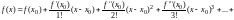
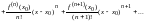Данный
ряд называется рядом Тейлора.При
данный ряд имеет вид
и
называется рядом Маклорена.Разложения
функций по данным формулам справедливы
только в области сходимости этих рядов.В
формуле Тейлора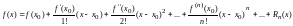
остаточный
член
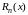можно рассматривать как остаточный
член ряда Тейлора. В форме Лагранжа он
имеет вид
,
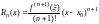где
или
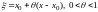.Также
для ряда Маклорена
остаточный
член в форме Лагранжа имеет вид
.Теорема
9.2. Для того
чтобы степенной ряд
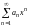сходился к функции
,
для которой он составлен, необходимо и
достаточно, чтобы остаточный член ряда
стремился к нулю при неограниченном
увеличении его номера n,
т. е.
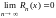.Д
о к а з а т е л ь с т в о. Необходимость.
Пусть ряд
сходится к функции
,
т. е.
.
Так как
,
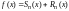то
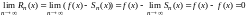
Достаточность.
Пусть
.
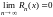Тогда
,
т.
е. ряд сходится.Разложение
в ряд Маклорена основных элементарных
функций.Принимая
во внимание полученные ранее формулы
Маклорена для функций
можем записать ряды для этих функций и
найти их области сходимости.Функция
.
Ряд Маклорена имеет вид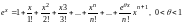
.
2.
Функция
.
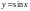Ряд Маклорена имеет вид
,где
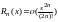
остаточный член, записанный в данном
случае в форме Пеано. Запись
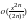означает, что функция
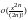является бесконечно малой по сравнению
с функцией
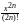.3.
Функция
.
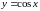Ряд Маклорена имеет вид
,где
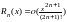
остаточный член. Здесь нумерация членов
ряда начинается с n
= 0. На основании теоремы Вейерштрасса
о равномерной сходимости любой степенной
ряд в интервале сходимости является
равномерно сходящимся. Поэтому ряд
составленный из интегралов членов
такого ряда сходится к интегралу от
суммы этого ряда