- •1. Дифференциальное исчисление
- •1.1. Пределы последовательности и функции
- •1.2. Производные
- •1.3. Исследование функций
- •1.4. Функция двух переменных
- •2. Интегральное исчисление
- •2.1. Неопределенный интеграл
- •2.2. Определенный интеграл
- •2.3. Несобственный интеграл
- •3. Элементы теории множеств и математической логики
- •3.1. Теория множеств
- •3.2. Булева алгебра. Алгебра высказываний
маОглавление
1. Дифференциальное исчисление 2
1.1. Пределы последовательности и функции 2
1.2. Производные 5
1.3. Исследование функций 8
1.4. Функция двух переменных 11
2. Интегральное исчисление 26
2.1. Неопределенный интеграл 26
2.2. Определенный интеграл 28
2.3. Несобственный интеграл 31
3. Элементы теории множеств и математической логики 33
3.1. Теория множеств 33
1. Дифференциальное исчисление
1.1. Пределы последовательности и функции
Основные определения, теоремы и формулы:
Иерархия
последовательностей по скорости
возрастания при
![]()
![]()
Данная запись означает, что
![]()
Иерархия элементарных
функций
![]() по скорости возрастания при
по скорости возрастания при
![]()
Данная запись означает, что
![]()
Замечательные пределы:
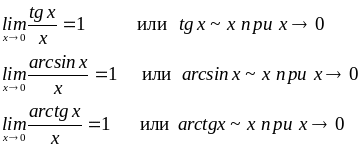
Знак «~» означает эквивалентность.
Например,
запись
![]() читается так:
читается так:
![]() эквивалентен
эквивалентен
![]() при малых значениях
.
при малых значениях
.
![]()
![]()
![]()
Примеры решения задач:
Пример 1: Вычислить предел функции
![]()
Решение: Выделяя
старшую степень в числителе и знаменателе
при
![]() ,
получим
,
получим
![]()
Пример 2: Вычислить предел функции
![]()
Решение:
Выделяя в числителе
и знаменателе функции, быстро стремящиеся
к бесконечности при
![]() (остальные функции будут бесконечно
малыми по сравнению с этими функциями),
получим
(остальные функции будут бесконечно
малыми по сравнению с этими функциями),
получим
![]()
Равенство нулю последнего предела вытекает из иерархии возрастания функции (см. Основные формулы)
Пример 3: Вычислить предел функции
![]()
Решение: Приведем
сначала подробное решение. Тождественными
преобразованиями сведем задачу к
вычислению замечательных пределов
![]()
При этом дважды использовался замечательный предел
![]()
Короткий способ
решения основан на использовании
эквивалентности
![]() при малых значениях
.
Используя малость
,
получим
при малых значениях
.
Используя малость
,
получим
![]() .
.
Тогда
![]()
Пример 4: Вычислить предел функции
![]()
Решение: Для
раскрытия неопределенности
![]() воспользуемся формулой сокращенного
умножения
воспользуемся формулой сокращенного
умножения
![]()
тогда
![]()
Далее, выделяя под знаком радикала главную степень при , получим
![]()
Короткая форма записи всех приведенных выше вычислений имеет вид
![]()
Другой способ решения использует замечательный предел
![]()
Для того, чтобы
воспользоваться этим соотношением
эквивалентности, вынесем из под знака
радикала
и используем малость величины
![]() .
Тогда получим
.
Тогда получим

1.2. Производные
Основные определения, теоремы и формулы
Определение
производной: Пусть
![]() определена в окрестности точки
.
Производной в точке
называется предел
определена в окрестности точки
.
Производной в точке
называется предел
![]()
Производные от элементарных функций
Производная от постоянной
![]()
Производная от линейной функции
![]()
Производная от степенной функции
![]()
Производная от показательной функции
![]()
Производные от тригонометрических функций
![]()
Производные от обратных тригонометрических функций
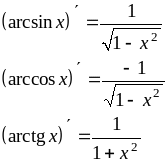
Производная от логарифмической функции
![]()
Правила дифференцирования
Линейность
![]()
Производная от произведения
![]()
Производная от частного
![]()
Производная от сложной функции
Пусть
![]() и
и
![]() .
Тогда возникает сложная функция
.
Тогда возникает сложная функция
![]() .
Производная от сложной функции будет
равна
.
Производная от сложной функции будет
равна
![]()
или
![]()
Правило Лопиталя для раскрытия неопределенности
Пусть
![]() ,
тогда если существует предел
,
тогда если существует предел
![]() ,
то существует
,
то существует
![]()
Примеры решения задач
Пример 1: Вычислить производную от функции
![]()
Решение: Воспользуемся
теоремой о сложной функции и табличными
производными:
![]()
Пример 2: Вычислить производную от функции
![]()
Решение: Воспользуемся формулой для производной от произведения функций
тогда
![]()
1.3. Исследование функций
Основные формулы
Теорема: Признаки возрастания и убывания функций
Если
![]() ,
то функция
возрастает в точке
.
,
то функция
возрастает в точке
.
Если
![]() ,
то функция
убывает в точке
.
,
то функция
убывает в точке
.
Определение: Если
в точке
![]() ,
то точка
называется критической (особой) точкой
функции.
,
то точка
называется критической (особой) точкой
функции.
Теорема: Достаточное условие существования экстремума
Пусть критическая (особая) точка функции т.е. .
Тогда, если при переходе через эту точку (слева - направо)
Производная
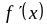 меняет знак с «+» на «-», то в точке
функция имеет максимум.
меняет знак с «+» на «-», то в точке
функция имеет максимум.Производная меняет знак с «-» на «+», то в точке функция имеет минимум.
Производная не меняет знака, то в точке - точка перегиба и экстремума в этой точке нет.
Теорема: Достаточное условие существования экстремума
Пусть критическая (особая) точка функции , т.е.
Тогда, если
Вторая производная
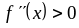 ,
то
- точка минимума.
,
то
- точка минимума.Вторая производная
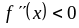 ,
то
- точка максимума.
,
то
- точка максимума.
Вторая производная
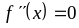 ,
то невозможно делать никаких выводов
без дальнейших исследований.
,
то невозможно делать никаких выводов
без дальнейших исследований.
Пример решения задач
Пример 1: Исследовать функцию
![]()
Решение:
Проверим четность функции
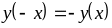 ,
т.е. функция нечетная, а ее график
центрально - симметричен.
,
т.е. функция нечетная, а ее график
центрально - симметричен.Предел функции при
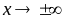 равен
равен
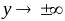 .
.Найдем корни функции

![]()
отсюда имеем три
корня:
![]() .
.
Найдем критические (особые) точки функции, в которых
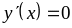
![]()
отсюда имеются
две критические точки:
![]()
В точке
![]() производная меняет знак с «-» на «+»,
следовательно
- точка минимума.
производная меняет знак с «-» на «+»,
следовательно
- точка минимума.
Аналогично,
![]() - точка максимума.
- точка максимума.
Найдем вторую производную
![]()
Вычислим вторую
производную в критических точках:
![]() ,
тогда
- точка минимума;
,
тогда
- точка минимума;
![]() ,
тогда
- точка максимума. Эти вычисления
подтверждают заключение предыдущего
пункта.
,
тогда
- точка максимума. Эти вычисления
подтверждают заключение предыдущего
пункта.
Вычислим значение функции в критических точках
![]()
Окончательно график функции имеет вид
![]()