Часть 4. Элементы теории графов.

 Понятия графа.

В этом параграфе дадим определение графа и свяжем это понятие с ранее изученным материалом.

Прежде всего вспомним понятие отношения:

Бинарным отношением R в множестве M называется подмножество его квадрата: RM².

Определение. Совокупность множества M с заданным на нем бинарным отношением RM² называется графом G=<M, R> M - множество вершин, R- множество ребер графа.

Г рафически это изображается с помощью точек и соединяющих их линий: точки соответствуют вершинам, линии- ребрам графа, примем не важно, как расположены точки и какие линии (прямые, кривые, длинные, короткие) их соединяют. Важно лишь, какие вершины соединены ребрами.

Пример. М={1,2,3,4,5}, R={(1,3), (1,2), (2,4), (4,4), (4,2)}.

Граф G=<M, R> выглядит так:

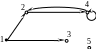
Существует большое количество понятий, описывающих части графа и видов. Основные понятия введем сейчас, остальные будем вводить по мере необходимости.

Основные понятия.

Если r={m_i, m_j} - ребро, то вершины m_i, m_j - концы ребра.

Если вершина является концом ребра, то говорят, что данная вершина и ребро инцидентны.

Две вершины называются смеженными, если они соединены ребром.

Два ребра называются смежными, если они имеют общую вершину.

По графу, полученному в примере, можно выделить еще группу новых понятий, Направленное (ориентированное) ребро называется дугой. А граф с ориентированными ребрами - ориентировочный.

Вершина, инцидентная только одному ребру, называется висячей. Вершина, которой не инцидентно ни одно ребро, называется изолированной.

ребро (Дуга) (m_i, m_j) называется петлей.

Ребра, инцидентные одной и той же паре вершин, называются кратными.

Свяжем понятия графа с материалом, изученным ранее.

Вспомним свойства отношений.

1. Отношение RM² рефлексивно, если mM справедливо: (m_i, m_j)R.

При задании рефлексивного отношения графом каждая его вершина будет иметь петлю:

2. Отношение RM² симметрично, если из (m_i, m_j)R следует (m_i, m_j)R m_i, m_jM, m_im_j.

При задании симметричного отношения графом, между каждой парой вершин, находящихся в отношении R, имеются две противоположно направленные дуги.

m_i

m_j

3. Отношение RM² транзитивно если из (m_i, m_j)R и (m_i, m_k)R следует, что (m_i, m_k)R m_i, m_j, m_kM, m_im_jm_k.

В графе, задающем транзитивное отношение R, для всякой пары дуг таких, что конец первой совпадает с началом второй существует третья дуга, имеющая общее начало с первой и общий конец со второй:

транзитивно замыкающее ребро.

Граф, каждая вершина которого соответствует одному из подмножеств n - элементного множества, будет иметь две вершины.

Пусть n=3, A={a,b,c}, M=P(A)={,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}

Отношение включения есть отношения частного порядка на множестве Р(А). То есть некоторые элементы Р(А) сравнимы по отношению включения ({a}{a,b}), некоторые не сравнимы ({a,b} и {b,c}).

Отношение частичного порядка обладает свойствами рефлексивности, антисиммертричности и транзитивности.

Граф, задающий частичный порядок на множестве Р(А) по отношению включения, будет содержать петли и транзитивно замыкающие ребра. Краткие ребра в нем отсутствуют.

Часто частного упорядоченное множество представляют в виде графа, у которого удалены все петли и транзитивно замыкающие дуги.

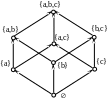
Графы такого вида задают решетки. Решетки - это множество с заданным на нем отношением порядка, любые 2 элемента которого имеют наименьшую верхнюю и наибольшую нижнюю грань. (этих элементов).

По виду данного графа мы определяем для любых двух элементов те, которые их покрывают, то есть включают в себя. Их пересечение и дает наименьшую:

Для элементов {a} и {b} наименьшая верхняя грань - {a} и {b} = {a,b}

наибольшая нижняя грань - {a}  {b}= .

{a,b} и {a,c} наименьшая верхняя грань - {a,b,c}

наибольшая нижняя грань - {a,b}  {a,c}= .

изображение при помощи граф – разложение подмножества по циклам.

Вопрос: Какое число различных графов можно построить на n вершинах и m ребрах?

Вершины не помечены (не различимы), ребра тоже.

Изобразим все принципиально различающие графы для n=4.

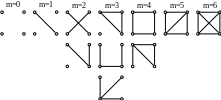
За полученное правильное и обоснованное решение - 1 балл на экзамене.