Связность. Компоненты связности.

Граф называется связным, если любая пара его вершин соединена маршрутом .

Связный ориентированный граф называется сильно связным.

Орграф называется слабо связным, если соответствующий ему неориентированный граф связный.

Максимальный по включению вершин связный подграф графа называется его компонентой связности.

Граф называется несвязным, если число его компонент больше одной.

Операция удаления вершины из графа - это удаление вершины с инцидентными ей ребрами (дугами).

Вершина графа, удаление которой увеличивает число компонент связности, называется разделяющей (или точкой сочленения).

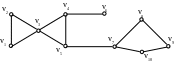
Точки сочленения – v₃, v₄, v₅, v₇.

Связностью графа называется наименьшее число вершин, удаление которых делает граф несвязным или тривиальным.

Количество компонент связности находится в определенном соотношении с основными параметрами - числом его вершин и ребер.

Утверждение. Пусть G - простой граф с n вершинами и K компонентами связности. Число ребер в таком графе не может превосходить величины .

Следствие. Граф с n вершинами и числом ребер, большим чем , связан.

Доказать самостоятельно.

Утверждение. Пусть G=<M, R> неориентированный граф с К компонентами связности: G₁=<M₁, R₁>,…, G_k=<M_k, R_k>. Тогда

1) M=M₁M₂…M_k, R=R₁R₂…R_k,

2) M_iM_j=, R_iR_j= при ij

3) Число вершин графа G равно количеству вершин всех его компонент; число ребер графа G равно числу ребер всех его компонент.

Матрица связности.

Пусть G=<M, R> - неориентированный граф, M={m₁,…,m_n}.

Матрицей связности графа G называется квадратная матрица S=[s_{i j}]порядка n, у которой

s_{i j}

1, если i=j или  маршрут, соединяющий m_i и m_j.

0, в противном случае.

то есть s_{i j} тогда и только тогда, когда вершины v_i и v_j принадлежат одной компоненте связности графа G.

Утверждение, позволяющее по матрице смежности графа получить матрицу связности.

Пусть G=<M, R>, где M={m₁,…,m_n} - граф без петель и с ребрами матрицы смежности А. Тогда матрица связности графа G

S=sign (E+A+A²+…+A^n-1), где E - единичная матрица порядка n.

операция перехода от произвольной матрицы с неопределенными элементами и матрице, состоящей только из 0 и 1.

Матрицей сильной связности орграфа Д называется квадратная матрица S(D)=[s_{i j}] порядка n, у которой А.

Говорят, что вершина w орграфа D (графа G) достижима из вершины v, если либо w=v, либо существует маршрут, соединяющий v и w.

Пусть D=<M, R> - орграф, где M={m₁,…,m_n}.

Матрицей достижимости орграфа D называется квадратная матрица T(D)=t_{i j} порядка n, у которой t_{i j}, если вершина v_j достижима из v_i и t_{i j}=0 - в противном случае.

Матрицей сильной связности орграфа D называется квадратная матрица S=[s_{i j}] порядка n, у которой s_{i j}, если вершина v_i достижима из v_j и долговременно достижима из v_i и s_{i j} - в противном случае.

Утверждение. Пусть D=<M, R> -орграф с матрицей смежности А. Тогда

1. T=sign (E+A+A²+…+A^n-1)

2. S=T&[T]^T, т – транспортирование, & - логическое умножение

Выделим компонент связности (алгоритм).

D=<V₁, R>

Алгоритм определения числа компонент сильной связности орграфа D, а также матриц смежности этих компонентов.

S - матрица связности, А - матрица смежности.

Шаг 1. Полагаем p=1, S₁=S.

Шаг 2. Включаем в множество вершин V_p очередной компонент сильной связности орграфа D вершины, соответствующим единицам первой строки матрицы S_p. В качестве A_p берем подматрицу матрицы смежности А, находящуюся на пересечении строк и столбцов, соответствующих вершин из V_p.

Шаг 3. Вычеркиваем из S_p строки и столбцы, соответствующие вершинам из V_p. Если в результате такого вычеркивания не останется ни одной строки (и соответственно ни одного столбца), то p - количество компонент сильной связности и A₁,…,A_p - матрица смежности компонент сильной связности D₁,…,D_p орграфа D.

В противном случае обозначим оставшуюся после вычеркивания из S_p соответствующих строк и столбцов матрицу через S_p+1, присваиваем p:=p+1 и переходим к шагу 2.